公路滑坡抗剪强度指标反算法应用研究

董书奎 袁铁权 李 杨

(1:吉林省高等级公路建设局，长春 130000;2:吉林省交通建设集团，长春 130000)

0 引言

在滑坡推力计算中，影响推力计算大小的土工参数主要有c(岩土体、滑带土的粘聚力)、φ(岩土体、滑带土的内摩擦角)和γ(岩土体的重度).γ通过试验或凭经验可以确定，且其选用值的误差对滑坡推力计算的影响远小于c，φ，滑带土的抗剪强度的取值成为影响滑坡推力计算结果可靠度的关键，因此计算推力时研究c，φ值的确定方法具有很大的实际意义.目前确定c，φ值的方法主要有试验手段、经验数据对比和反算法，试验法受多种条件的限制，难以模拟滑坡体实际的载荷或应力条件，而经验数据对比法过多的强调经验，因此反算法便成为人们常用的一种方法，试验指标仅为参考.

本文依托实体工程，介绍在一个滑体上截取若干剖面，分别采用简化反算法和多维图解反算法求解滑坡滑带土的抗剪强度指标c，φ值，并进行综合对比分析，研究反算法在计算公路滑坡抗剪强度指标中的工程应用价值.

1 基本原理和方法

反算法又称反演分析法或逆演法，它是在极限平衡原理的基础上，假定边坡处于极限平衡状态，此时边坡稳定安全系数为K，用边坡滑动力与抗滑力的平衡，计算滑动带土的抗剪强度指标.反算法的常用公式源于边坡稳定分析的各种演变公式，由于滑坡地质情况、简化条件的不同，存在着多种反算法，在具体的工程应用中应合理选择［1］.下面就对实际工程中常用的反算法进行介绍.

1.1 简化反算法［2］

对于我国绝大多数滑坡的滑动带多为折线形，各分段的下滑力和抗滑力不在同一直线上，为简化问题，可令:

简化反算法是根据式(1)，选定合理的滑动断面，并由滑坡所处的稳定状态，先确定安全系数K，然后反求出式中各滑带强度水平投影总和S中的抗剪强度指标c，φ值.为保证滑面抗剪强度的充分发挥，以得到正确反映土的力学性质的指标，一般选取处于或接近处于极限平衡状态下的滑坡断面进行反算，对产生过滑动的滑坡，需要恢复其滑动前的原断面再反算滑带土的抗剪强度指标.该法是工程中较常用的一种方法.

对大多数土体而言，采用同时考虑粘聚力和内摩擦力时的综合c，φ法［3］，其计算公式为:

式中，Wi为滑体下滑段第i条块所受的重力，kN;Wj为滑体抗滑段第j条块所受的重力，kN;αi为滑体下滑段第i条块所在折线段滑面的倾角，°;αj为滑体抗滑段第j条块所在折线段滑面的倾角，°;li为滑体下滑段第i条块所在折线段滑面的长度，m;lj为滑体抗滑段第j条块所在折线段滑面的长度，m;c为折线滑面上的综合单位粘聚力，kN/m2;φ为折线滑面上的综合内摩擦角，°;m，n为滑体下滑段和抗滑段的分块数.

在工程实际中，应用式(2)，选取断面按上述反算方法进行反算.

1.2 多维图解反算法

传递系数法适用于任意形状的滑动面，它假定条间力的合力与上一条土条底面相平行，根据力的平衡条件，逐条向下推求，直至最后一条土条的推力为零.

已滑动过的滑坡，在其上一次滑动或近期滑动处，即将要滑动而尚未滑动时，是处于极限平衡状态的.在其上所取的断面，应属于极限平衡状态的断面.据此断面建立的推力计算公式中最后一条土条的剩余下滑力应等于零，即:

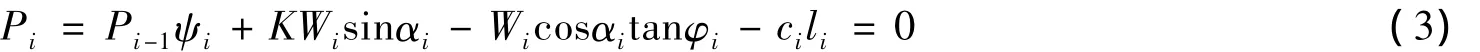
式中，Pi为第i个滑块的剩余下滑力，kN;ψi为传递系数，即:ψj=cos(αi-αi+1)-sin(αi-αi+1)tanφi+1;其余符号意义同前.

令K=1，由一个断面可以得到一个c，φ为未知数的方程，可以由一个值反算另一个;如果在滑坡体中找出两个或更多极限平衡状态的断面，方程则不止一个，利用这些方程联立求解，便可以解出c，φ这两个未知数.取两个断面的方程组为:

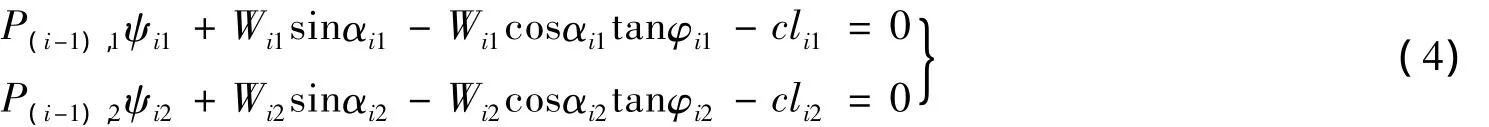
在上述计算公式中，Pi与Pi-1是逐次迭代的关系，传递系数ψi中也含有未知数φ的正切函数tanφ，所以在方程组的求解过程中会出现tanφ的高次幂函数，具体求解是非常困难的，可以采用多维图解法进行求解.

由式(3)可得:

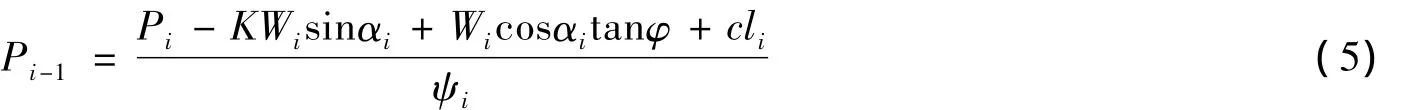
令最后一块土条的推力Pn=0，逐步递推计算可得:

同时，由式(3)亦可得:

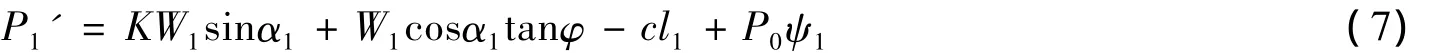
其中，P0=0.令:

当滑坡处于极限平衡状态时(即K=1.0)，任意给定一个c或φ值，由式(8)可求得一个相应的φ或c值，使G=P1-P1'等于或近似等于零.因此，可分别求解出每个断面在极限平衡状态时的数对c，φ值.将两个不同断面的这些对c，φ值分别绘制在安全系数K=1.0的平面上，可得到两条相交的c-φ值曲线，交点处的一组c，φ值即为多维图解反算法求解联立方程组所得的唯一解.

2 工程实例计算与分析

2.1 工程概况

吉林省某高速公路滑坡为剥蚀丘陵地貌，其最高地面高程为172.00 m，最低地面高程为149.00 m，相对高差为23.00 m，地形起伏不大，坡度为20°～30°.该滑坡平面形态呈半圆弧形，滑坡主轴与路线呈86.20°夹角，滑坡主轴长约40.5 m，滑坡前缘最宽处为119.1 m;滑坡上段表面覆盖有一层约2 m厚的亚粘土，滑体最厚处有13.85 m，滑坡滑向为32°;滑坡后缘距路基中线约52 m;滑坡周边范围内裂缝发育，见多条宽约10 cm～50 cm的裂缝，形成两个滑坡台阶;滑坡体积约28 000 m3，属中型滑坡.滑坡严重影响了该公路的正常使用.

2.2 计算断面选取

计算中可以选取一个断面进行反算，此时对一个断面反算时，常常需要根据滑带土条件和滑动瞬间的含水情况，以及参照类似的土质情况的有关资料，假定其中一个变化幅度不大容易掌握其范围者，来反求另一个;也可对多个断面建立联立方程同时反求主滑段的c值和φ值，要采用类似条件下两个或多个断面方程联立求解的方法，并要求这些断面的地质条件(滑面的物质组成和含水状态)、滑坡状态、滑动过程和滑坡发育阶段等类似;另外，还可以在同一次滑动中，找出两个相邻近的瞬间滑动计算断面，建立两个反算式，联立求解.

通过分析实体工程的地质情况及滑坡特点，选取该滑坡的典型断面1-1，2-2，采用简化反算法和多维图解反算法分别反算滑带土的c，φ值.

2.3 简化反算法反算

根据滑坡的性质，采用简化反算法中的综合c，φ法反算滑带土的抗剪强度指标.考虑到滑坡已有数次蠕滑但还没有到加速滑动状态，取K为0.97.

(1)1-1断面

对1-1断面进行反算，所需各项数据如表1所示，断面图如图1所示.

图1 滑坡1-1断面

表1 1-1断面滑坡数据

计算得:

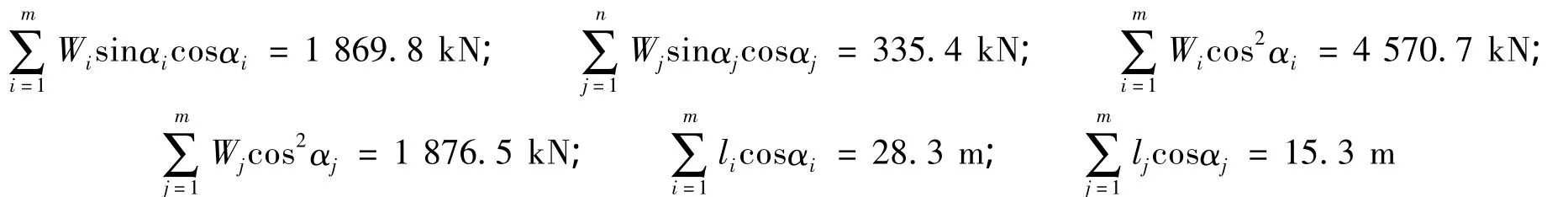
将以上数据代入式(2)中并整理得:

(2)2-2断面

对2-2断面进行反算，所需各项数据如表2所示，断面图如图2所示.

图2 滑坡2-2断面

表2 2-2断面滑坡数据

计算得:

将以上数据代入式(2)中并整理得:

联立方程(9)和(10)解得:tgφ=0.208，φ=11.78°，c=3.1 kPa.

即简化反算法求得该滑坡的抗剪强度指标值:c=3.1 kPa，φ=11

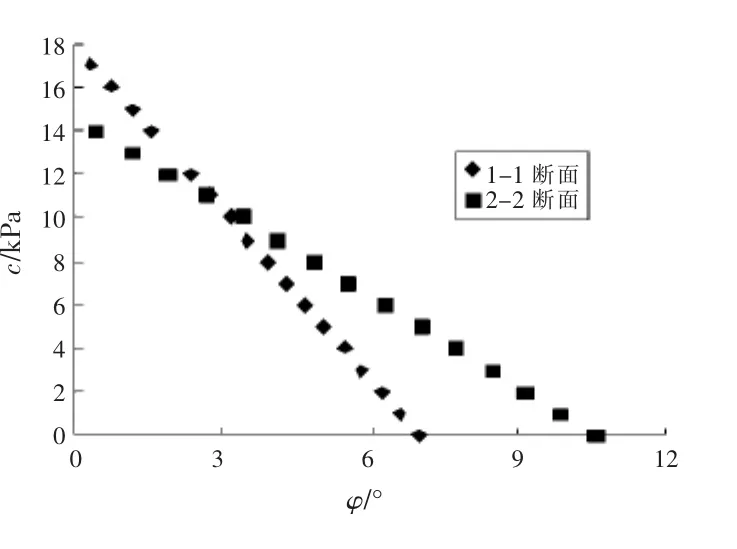
图3 c-φ关系曲线

2.4 多维图解反算法反算［4］

对1-1断面、2-2断面采用多维图解反算法反算滑坡滑带土的抗剪强度指标.

(1)1-1断面

对1-1断面，所需数据见表1，带入公式(6)～(8)计算得:

求得的c-φ值的关系曲线如图3所示

(2)2-2断面

对2-2断面，带入公式(6)～(8)计算得:

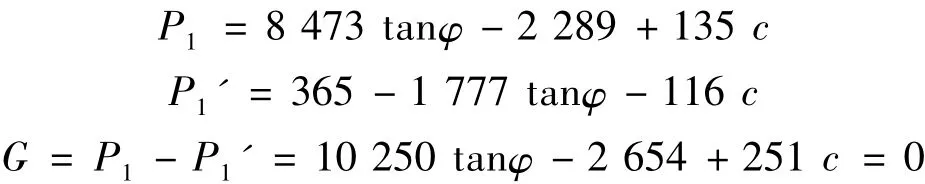
求得的c-φ值的关系曲线 如图3所示.

图3中两曲线交点处数值即为反算得的抗剪强度值，即:c=2.86 kPa，φ=11.1°.

2.5 对比分析

采用简化法、多维图解反算法和室内试验方法获得的滑坡滑带土抗剪强度指标对比见表3.

表3 反算抗剪强度指标对比

从表3可以看出，两种方法对滑带土抗剪强度指标的反算值比较接近，考虑到计算过程中的计算误差等影响因素，可以认为两者抗剪强度指标反算值一致，与室内试验结果有一定差距.但考虑取样及试验条件不可能与滑坡滑动时的现场条件完全一致，反算法计算结果与室内试验结果相近，且更接近于工程实际，具有一定的可靠度，可供工程技术人员实际应用，特别是更加简便易行的多维图解反算法.

3 结语

根据上述分析，滑坡的抗剪强度指标由于受到试样与试验条件的约束，试验测试结果通常不尽人意，而简化反算法及多维图解反算法应用简便，精度满足工程要求.因此，运用反算法综合考虑环境与地质因素的影响，可获得真实可靠的滑坡滑带土的抗剪强度指标，为公路工程滑坡的预防与治理提供科学的依据，具有重要的工程意义和实用价值.

［1］程嫒彩，戴自航.多剖面反算滑带土抗剪强度指标的研究［J］.土工基础，2006，27(10):1811-1814.

［2］郑明新.论滑带土强度特征及强度参数的反算法［J］.岩土力学，2003(4):528-532.

［3］交通部第二公路勘察设计院.公路设计手册《路基》(第二版)［M］.北京:人民交通出版社，1996:239-240.

［4］李 凡，孙四平.多维图解反算法确定膨胀土滑坡土体的抗剪强度指标［J］.岩石力学与工程学报，2004，23(12):2042-2045.