南京市房地产价格预测

□文/ 李 辉 徐 霞 何 芳

（1.南京工业大学 江苏·南京；2.江苏省江阴市申港财政所 江苏·江阴）

引言

随着中国改革开放的发展，人民生活水平不断提高，社会主义市场经济日趋完善，房地产业也蓬勃发展，但随着房地产领域的投机愈演愈烈，造成房价虚高，泡沫增大，楼市的泡沫已经严重影响到国民经济的健康发展。国家和地方政府开始对房价进行宏观调控，出台了一系列政策，房价过快上涨的势头得到有效遏制。应住建部要求，南京市政府在2011年2月底颁布了城市住房限购令细则，楼市开始逐步退热。有些观点认为，房价已经到了拐点，会持续下降；也有观点认为，此次房价波动只是暂时的。当下，房价的走势已经成为研究的热点。对房价涨跌走势的判定以及对房地产价格的预测，不仅与每一个需要买房的个体有关，还关系到房地产企业的销售业绩、其对市场的把握、经营策略的调整、企业的生存，更关系到国家宏观政策的实施的反应和后续政策的制定和实施以及整个国民经济的健康发展。

目前，学界对房地产价格预测采用了多种方法。Brunsdon 和Fotheringham 以英国Kent 郡为例，采用地理加权回归（GWR）模型探讨房价与楼地板面积之间的关系；罗罡辉等将GWR 模型应用于杭州市住宅地价的研究中，分析了宗地面积对住宅地价影响的空间差异性，并与特征价格模型进行了对比；王凌云采用了灰色GM（1，1）模型预测分析了宁波市商业地产价格；李东月和马智胜的灰色GM（1，1）模型在房价预测中的算法研究，预测了长春市房地产价格变动趋势。综合来看，采用目前的方法进行房价预测时，主要遇到数据分布不明显、预测精度要求高等难点。而灰色马尔科夫链模型在灰色GM（1，1）模型的基础上，使用马尔科夫链的状态转移概率修正预测结果，进一步提高灰色GM（1，1）的预测精确性，同时这种模型保留了灰色GM（1，1）模型的对样本数据需求量小、分布规律性要求不严、短期预测精度较高等优点。因此，本文采用了灰色马尔科夫链模型对南京房地产价格进行预测，并且本文通过对南京市从2010年第4 季度至2011年第4 季度的房地产平均价格进行预测来验证该模型的有效性，同时利用灰色马尔科夫链模型预测了2012年4 个季度南京房地产价格的趋势。

一、基于灰色GM（1，1）模型的价格预测

首先建立灰色GM（1，1）模型对n 个季度内的房产价格进行预测，详细的建模过程如下：

（1）假设第t 个季度的价格为pt，且t＝1，2，3，…，n，则n 个季度内的价格序列为：P（0）＝（p1（0），p2（0），pt（0），…，pn（0））。

（2）采用1-AGO 生成一阶累加生成序列：

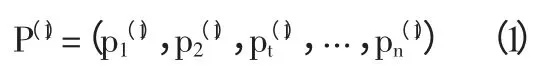
（3）对累加生成序列建立一阶微分方程，则有：

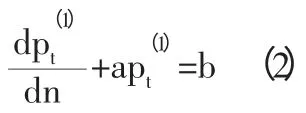
其中，a 为发展系数，b 为灰色作用量。

采用最小二乘法对式（2）求解得出：

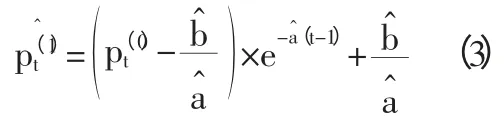
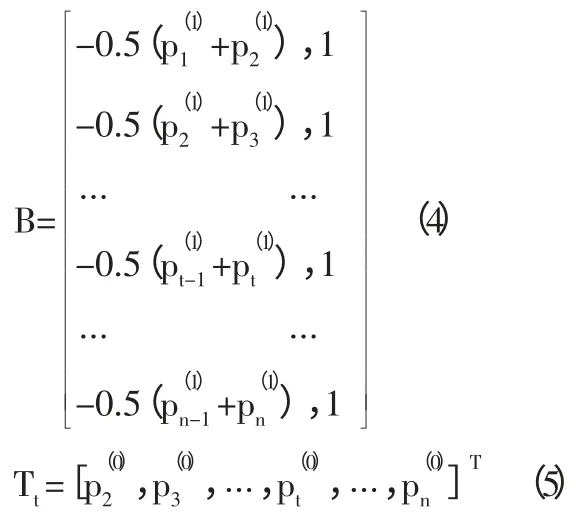
根据式（3）得出预测价格序列：

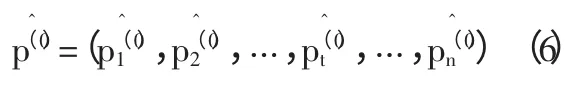
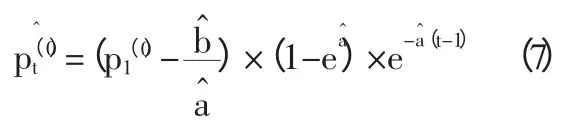
该式则为价格的预测公式。

二、基于灰色马尔科夫链模型的价格预测

灰色马尔科夫链模型是灰色GM（1，1）和马尔科夫链预测的结合。这种模型保留了灰色GM（1，1）预测的优点，即样本数据需求量小、对分布规律性要求不严、短期预测精度较高；同时根据状态之间的转移概率修正预测结果，进一步提高了预测的精确性。以下是马尔科夫链预测模型对房地产价格预测的详细过程。

预测状态划分后，需要构造状态转移概率矩阵。设状态Qi经过t 步转移到Qj的数量为nij（t），状态Qi出现的数量为ni，那么Qi状态经过t 步转移到Qj的状态转移概率为：

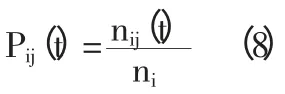
由此获得m×m 阶状态转移概率矩阵为：

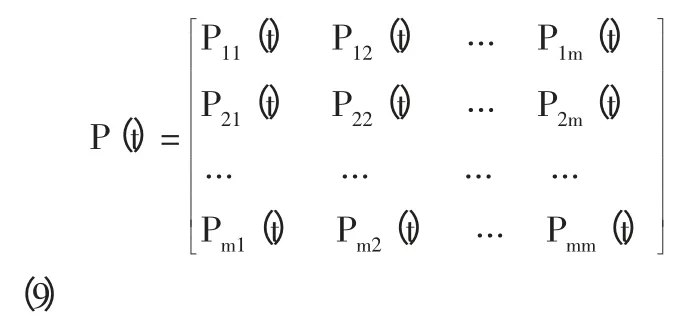
当未来的转移状态Qt+1确定后，就可以对需要预测的价格即t+1 时刻的价格pt+1进行预测。pt+1的取值区间为［⊗1（t+1），⊗2（t+1）］，则预测价格则为该区间中点，即：

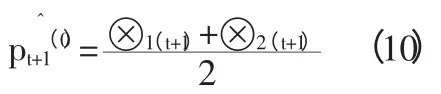
三、利用灰色马尔科夫链模型预测南京房地产价格

本文将使用灰色马尔科夫链模型对南京市从2010年第4 季度至2011年第4 季度的房地产平均价格进行预测，具体数据如表1 所示。（表1）其中，该表中的数据是南京八大板块的房产平均价格，原始数据来源于House365 网站（http：//www.house365.com）。

首先建立灰色GM（1，1）模型。根据表1，生成价格序列P（0）：

P（0）＝（p1（0），p2（0），…，p‘t（0），…，pn（0））＝（9867.458，10574.958，10635，10631.875，10328.33）

按照式（2）到（7）进行求解，最后得出灰色GM（1，1）模型的价格预测函数为：

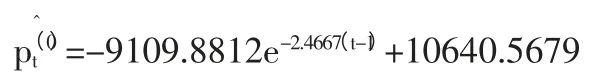
建立灰色GM（1，1）模型得出预测函数后，对这5 个季度进行预测，得出的结果见表2。（表2）然后，使用灰色马尔科夫链模型对该函数进行修正。根据预测误差率，可以划分4 个状态：

Q1：

Q2：

Q3：

Q4：

根据GM（1，1）模型的预测函数给出的结果（见表2），除最后一个季度外的其他4 个季度分别落入Q1、Q2、Q3、Q4的数量为0，2，1，1。之所以将最后一个季度排除在外，是由于该季度未来状态转移情况不明。根据式（8）、（9）得出状态转移概率矩阵：

得出状态转移概率矩阵后，根据式（10）对GM（1，1）模型预测的数据进行修正，结果见表2。可以看出，相比灰色GM（1，1）模型，灰色马尔科夫链模型预测的误差率更低，具有良好的预测效果，基本达到预测目标。

通过对南京市从2010年第4 季度至2011年第4 季度的房地产平均价格的预测，验证了灰色马尔科夫链模型比灰色GM（1，1）有更好的效果。因此，本文将采用灰色马尔科夫链模型对2012年4 个季度的南京房地产平均价格进行预测，具体步骤同上文，结果如表3 所示。（表3）

表1 2010年第4 季度至2011年第4 季度南京市房地产平均价格表

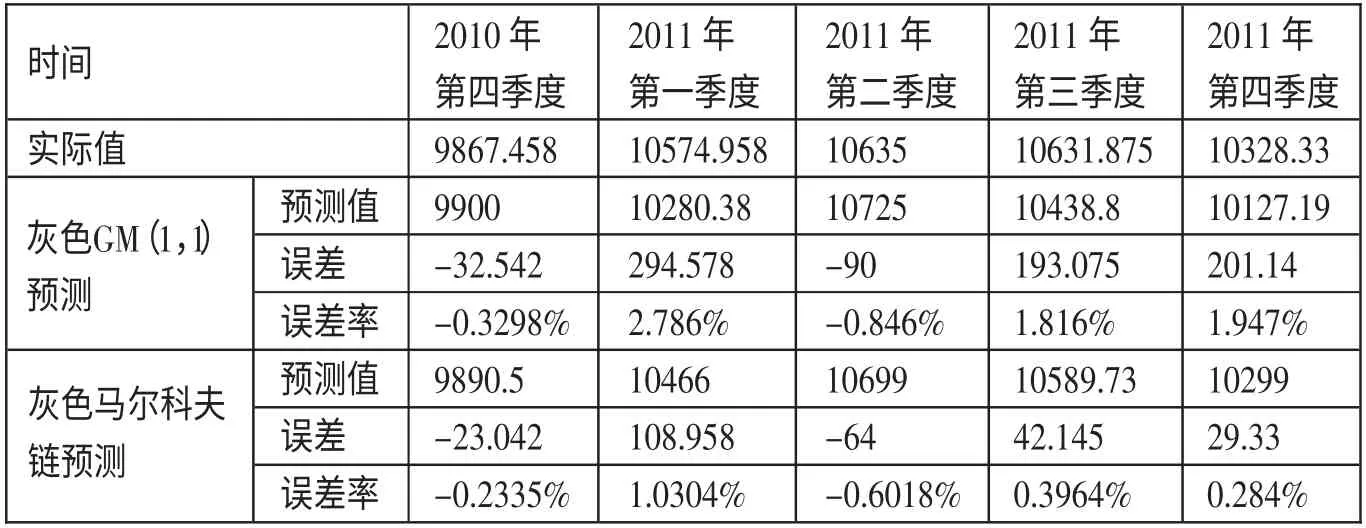
表2 GM（1，1）与灰色马尔科夫链模型的误差比较

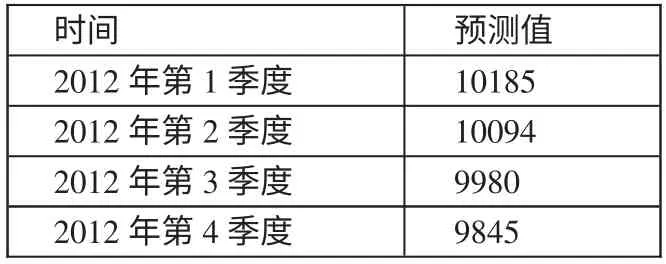
表3 2012年南京市房地产平均价格走势表

根据灰色马尔科夫链模型对2012年4 个季度的价格预测可以发现，房价既不是波动也不是急剧下降，而是在稳步缓慢下降。一方面在模型上验证了目前房地产严控政策的成效；另一方面可以认为，如果延续当前严控政策，模型预测得到的结果将很有可能在现实中出现。

四、结论

针对当前房地产严控环境下，房地产价格的走势已成为当前学界的研究热点，本文采用了灰色马尔科夫链模型对灰色GM（1，1）改进，提高了预测精度，并通过对南京市从2010年第4 季度至2011年第4 季度的房地产平均价格的预测验证了其有效性。并采用该模型对2012年4个季度的南京房地产价格进行预测，从预测结果中发现房价既不是波动也不是急剧下降，而是在稳步缓慢下降。

根据模型预测结果，当前房地产调控政策是有效的，将使房价稳步降低，而不会引起房地产市场的崩溃，也不会导致房地产价格的报复性反弹。从长远来看，此次调控实际上是对房地产业健康良性可持续发展的重要手段。只有当房价回归合理水平，真正需要买房的需求得到满足，房地产业才能够健康发展。在一个良性发展的社会中，不断增长的人口以及人民群众不断增加的物质需求，房地产业的主体需求还是存在的。房地产企业要认清市场的走势，在危机面前不要退缩，一方面要合理的降低成本，加速资金周转，提高企业运行效率；另一方面要生产出符合市场需求的建筑产品，把危机转化为机遇。

[1]Brunsdon C，Fot heringham A S.Some notes on Parametric significance tests for geographically weighted regression [J].Journal of Regional Science，1999.39.

[2]罗罡辉，吴次芳，郑娟尔.宗地面积对住宅地价的影响[J]. 中国土地科学，2007.10.

[3]王凌云. 基于GM（1，1）模型的宁波市商业地产价格预测 [J]. 区域经济，2011.10.

[4]李东月，马智胜.灰色GM（1，1）模型在房价预测中的算法研究[J]. 企业经济，2006.9.

[5]刘思峰.灰色系统理论及其应用（第4版）[M].科学出版社，2008.12.1.