一类新超混沌系统的同步与反同步

张树来

（常熟理工学院数学与统计学院，江苏常熟 215500）

一类新超混沌系统的同步与反同步

张树来

（常熟理工学院数学与统计学院，江苏常熟 215500）

以一类新超混沌系统为例，研究了驱动系统和响应系统的同步与反同步问题，利用Lyapunov稳定性理论设计了控制器，实现了它们的同步与反同步，数值模拟结果验证了该方法的有效性.

超混沌系统；Lyapunov函数；同步；反同步

从1963年Lorenz在实验中发现第一个混沌吸引子以来，Lorenz系统就被作为第一个研究混沌的物理和数学模型，成为后人研究混沌理论的出发点和基石.在过去的几十年里，混沌控制与同步的理论在一些工程领域中得到了广泛的应用，如图像加密，保密通信和信息工程等，显示出了重要的应用价值[1-2]，所以对混沌控制与同步的理论研究已成为非线性控制理论研究的热点之一.由于混沌系统对初值极其敏感性，所以长期以来人们认为混沌系统是不可控制的，混沌同步就更加难以实现.自从Pecora和Carroll[3]在1990年利用电路实现混沌同步以来，混沌同步受到了各个领域学者的广泛关注.随着混沌控制与同步研究的不断深入，如广义同步、完全同步、耦合同步和超混沌系统同步方案[4-7]，近来又提出了混沌系统的反同步[8]等.

目前对于混沌控制与同步研究方法很多，但是对于超系统之间的同步与反同步研究相对较少，在实际应用中特别是两个超混沌系统的同步与反同步容易应用于安全通信中，因此考虑两个超混沌系统的同步与反同步更具有重要的实用价值.本文利用Lyapunov的理论设计了相应的控制器，实现了两个超混沌系统的同步与反同步，并利用matlab工具进行了数值仿真，验证了其有效性.

1 系统模型

最近，T.Wang等人研究了一类新的四维超混沌系统[8]，系统如下：

这里x1,x2,x3和x4为变量，a,b,c,d为参数.当a=2.1,b=0.6,c=30,d=0.7时，（1）为超混沌系统.图1为超混沌系统（1）的吸引子.

图1 当a=2.1,b=0.6,c=30,d=0.7时超混沌系统（1）的吸引子

2 驱动系统和响应系统的同步及数值仿真

将系统（1）作为驱动系统，相应地响应系统为：

此处ui(i=1,2,3,4)为控制器.令系统（1）与系统（2）的同步误差为：

我们构建Lyapunov函数为：

故

此时若取

即在控制器（7）的作用下，两个超混沌系统对应的时间序列可以达到同步.采用Runge-Kutta方法模拟，驱动系统和响应系统初值选为：x1(0)=100,x2(0)=5，x3(0)=100,x4(0)=-10，y1(0)=30,y2(0)=20,y3(0)=20,y4(0) =8，数值模拟得误差随时间变化如图2所示.由图2可见，e1,e2,e3,e4很快趋于0，系统达到了同步.

图2 系统（1）与（2）对应时间序列同步误差曲线

3 驱动系统和响应系统的反同步及数值仿真

仍然将系统（1）作为驱动系统，（2）为响应系统，令系统（1）与系统（2）的同步误差为：

构建（5）式的Lyapunov函数，则

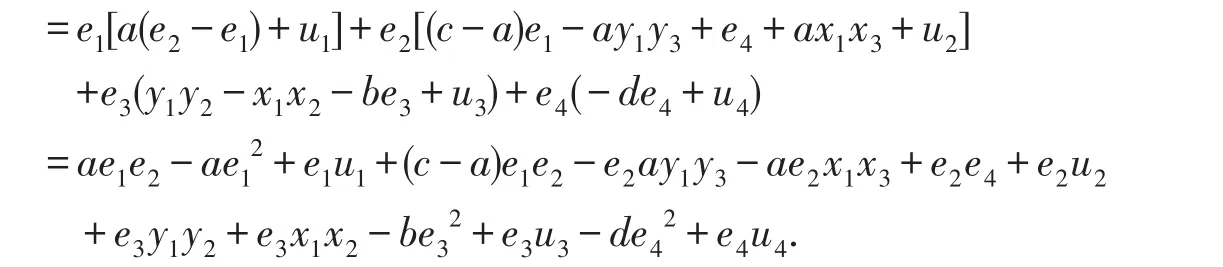
即在控制器（10）的作用下，驱动系统（1）与响应系统（2）达到了反同步.采用四阶Runge-Kutta方法模拟，驱动系统和响应系统初值选为：x1(0)=-10,x2(0)=-5，x3(0)=10,x4(0)=-10，y1(0)=21,y2(0)=20,y3(0)= 8,y4(0)=-9，数值模拟得误差随时间变化如图3所示.由图3可见，e1,e2,e3,e4很快趋于0，系统达到了同步.

图3 系统（1）与（2）对应时间序列反同步误差曲线

4 结论

本文首先介绍了混沌及同步方法的内容，然后主要利用Lyapunov稳定性理论，根据实际情况设计了适当的控制器，对一类新的四维超混沌系统[9]与其对应响应系统的时间序列同步与反同步进行了研究，并利用matlab等工具进行了数值仿真，验证了其可行性与有效性.由于该方法设计的控制器比较简单，因而在实际工程应用中更容易实现，具有一定的应用价值.

[2]Park J H.On synchronization of unified chaotic systems via nonlinear control[J].Chaos Solitons Fract,2005,25:699-704.

[3]Pecora L M,Carroll T L.Synchronization in chaotic systems[J].Phys Rev Letter,1990,64(8):821-824.

[4]张树来，吴志明.一个新时变混沌系统的耦合同步[J].常熟理工学院学报，2007，21（10）：24-28.

[5]Mahmoud G M,Mahmoud E E.Complete synchronization of chaotic complex nonlinear systems with uncertainparameters[J].Nonlinear Dyn,2010,62:875-882.

[6]Kocarev L,Parlitz U.General Approach for Chaotic Synchronization with Applications to Communication[J].Phys Rev Lett,1995, 74(6):5028-5031.

[7]于灵慧，房建成.Hénon混沌同步的自适应逆控制[J].控制理论与应用，2005，22（4）：623-626.

[8]Kim C M,Rim S W,Kye W H,et al.Anti-synchronization of chaotico scillators[J].Physics Letters A,2003,320(1):39-46.

[9]Wang T,Jia N.Chaos control and hybrid projective synchronization of several new chaotic systerms[J].Applied Mathematics and Computation,2012,218:7231-7240.

[1]Zhang D,Xu J.Projective synchronization of different chaotic time-delayed neural networks based on integral sliding mode controller[J].Appl Math Comput,2010,217:164-171.

Synchronization and Anti-synchronization in a Class of New Hyper-chaotic System

ZHANG Shu-lai
(School of Statistics and Mathematics,Changshu Institute of Technology,Changshu 215500,China)

In this paper,the definition of chaos is introduced,and these methods of chaotic synchronization are recommended.Then,as an example of a class of new hyper-chaotic system,chaos synchronization and anti-synchronization of the drive system and the slave system are investigated.With the Lyapunov stability theory,the controller is constructed analytically to synchronize and anti-synchronize them.The numerical simulation results show that the proposed scheme is effective.

TP273；O415.5

A

1008-2794（2012）10-0032-05

2012-09-11

常熟理工学院青年教师科研启动基金资助项目“一类混沌系统的控制与同步”（QZ1204）

张树来（1978—），男，山东临沂人，讲师，硕士，研究方向：混沌动力学．

Key words:hyper-chaotic system;Lyapunov function;synchronization;anti-synchronization