V-BLAST OFDM 信号调制识别算法

战金龙,郭永明,卢建军

(1.西安邮电大学 通信与信息工程学院,西安710061;2.国家无线电频谱管理研究所, 西安710061)

1 引 言

垂直分层空时结构(Vertical Bell Labs Layered Space-Time,V-BLAST)作为一种多输入多输出(Multiple-input Multiple -output,MIMO)技术,利用多个天线实现多发多收,在不需要增加频谱资源和天线发送功率的前提下,可以成倍地提高信道容量[1-4]。OFDM(Orthogonal Frequency-Division Multiplexing)技术将频率选择性衰落信道转化为若干个平坦衰落的子信道,可以有效地抵抗频率选择性衰落[5]。因此,充分开发这两种技术的潜力,将两者结合起来的V-BLAST OFDM 技术已成为第4 代移动通信核心技术的解决方案,也是目前研究的热点[6]。所以,在未来的移动通信中, V-BLAST OFDM 调制信号必然是通信信号的重要组成部分。

调制信号识别能够在没有任何先验知识的条件下自动识别信号的调制方式, 在多体制通信、软件无线电、电子侦察和电子监听等领域有重要作用。目前, 国内外对单载波数字调制信号在加性高斯白噪声信道中的调制方式盲识别技术进行了广泛而深入的研究[7-12], 并取得了良好的识别效果, 但是针对OFDM 信号尤其MIMO-OFDM 信号调制盲识别的研究较少。文献[ 13] 提出了基于高阶累积量的SFBC-OFDM 信号调制识别算法,仅针对2 发1 收的Alamouti 编码结构。

本文提出了频率选择性衰落信道下基于高阶累积量的V-BLAST OFDM 信号调制盲识别算法,对于V-BLAST 结构,给定集合{MFSK,MPSK,MQAM,OFDM}进行多载波与单载波的类间识别。

2 系统模型和传统的检测方法

V-BLAST 单载波信号和V-BLAST OFDM 多载波信号发射机和接收机结构分别如图1 和2 所示。

图1 V-BLAST 单载波系统结构框图Fig.1 Block diagram of V-BLAST single carrier system

图2 V-BLAST OFDM 多载波系统结构框图Fig.2 Block diagram of V-BLAST OFDM system

假设发射天线个数为n,接收天线个数为m 。发射的数据序列S 解复用为n 层,第i 层的数据为Si,对于V-BLAST 单载波信号Si直接由第i 个发射天线发射,接收天线j 接收的第p 个V-BLAST 单载波信号可以表示为

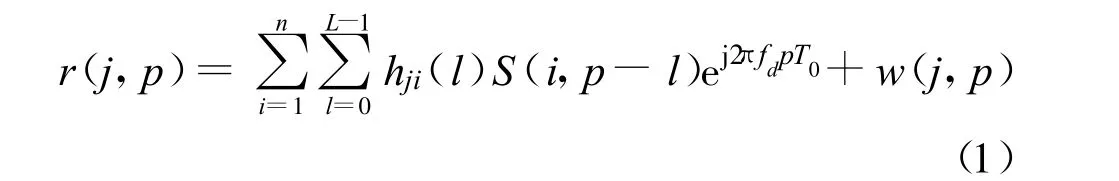
式中,w(j,p)表示噪声分量,服从均值为0、方差为σ2w的高斯分布;hji(l),l=0,1, …L -1 表示第j 个接收天线与第i 个发射天线之间的频率选择性衰落信道的第l 条路径的衰落系数(共L 条多径),服从复Rayleigh 分布;fd表示Doppler 频移。单载波信号S 的可能集合包括{sMPSK(t),sMQAM(t),sMFSK(t)},信号表达式如下:

式中,A、Ts、f c 分别表示接收信号的幅度、码元周期、载波频率,ck、mk、ak表示各种调制方式的传输符号,Δf 0 为频率间隔,g(t)为脉冲成形函数。

对于V-BLAST OFDM 信号,第i 层的数据为Si则需经过串/并(S/P)转换后, 变为n 个并行的符号,然后进行OFDM 调制,由第i 个发射天线发射,接收信号的形式与V -BLAST 单载波信号相同。OFDM 信号的表达式为

式中,sn,k表示OFDM 调制前的传输符号,N 表示子载波个数。发射信号、信道衰减因子以及高斯白噪声互相独立。

3 基于高阶累积量的V-BLAST OFDM 多载波信号调制识别

直接对接收的数字中频信号进行处理。令

则r(j,p)=v(j,p)+w(j,p),考虑到各发射天线和接收天线之间的信道衰落系数相互独立,信道衰落系数与信号之间也相互独立,v(j,p)的各阶矩为

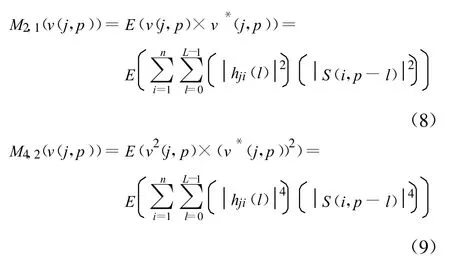
由于hji=αji+jβji, αji和βji相互独立并同时服从均值为零、方差为σ2h的正态分布,则:

Rayleigh 信道衰落系数hji具有如下特点[14]:

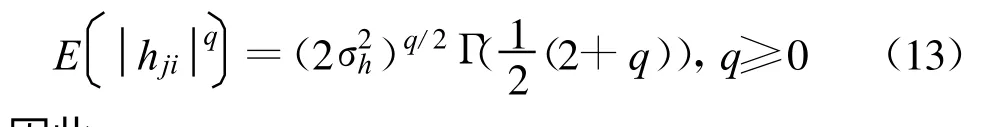
因此,

代入式(7)～(9),v(j,p)的各阶矩可以表示为

v(j,p)的各阶累积量为

接收信号r(j,p)的二阶累积量为

当SNR 足够大时, 噪声可以忽略。此时,C2,1(r(j,p))≈2nLσ2hM 2,1(S)。由于高斯噪声二阶以上的累积量恒为0,所以,r(j,p)的四阶累积量为

从式(19)和(20)可以看出,r(j,p)的各阶累积量都与频率选择性衰落信道以及发射信号调制类型有关,为了消除频率选择性衰落信道的影响,选取特征参数d20,d20由下式给出:

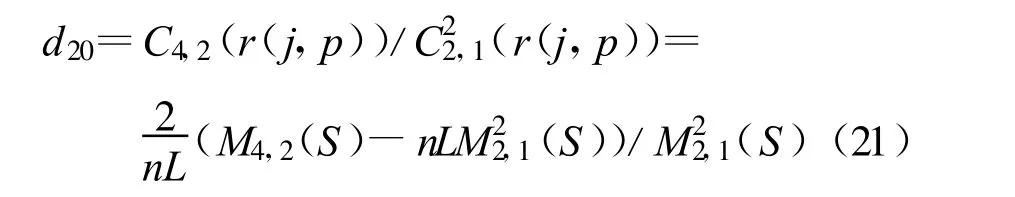
根据文献[13]单发单收下d20的结果,不难计算本文4 个发射天线下,d20(OFDM)=0.5/L ,d20(MFSK)=0, d20(MPSK)=0, d20(64QAM)=0.189/L,d20(128QAM)=0.176/L。此时的门限值应设为(0.5+0.189)/(2×L),即当高于该门限时就认为是OFDM 调制,否则为单载波调制。然而,计算r(j,p)的二阶累积量C2,1(r(j,p))时忽略了噪声能量,因此各调制方式的d20值实际上都略小于上面计算的理论值,因此门限值需设置得略小,这里设置为(0.5+0.189)/(3×L)。

算法流程如图3 所示。可以看出,算法中最重要的步骤就是上面提出的计算各种调制方式的特征参数d20。

图3 V-BLAST OFDM 多载波信号识别算法流程图Fig.3 Flow chart of the proposed recognition algorithm

4 仿真结果

仿真条件如下:以4 发4 收的V-BLAST 结构为例,每种调制方式取4 096个数据,经过解复用后每个发射天线的数据为1 024,OFDM 子载波个数为1 024,所有子载波均采用16QAM 调制,进行500 次的Monte-Carlo 实验,SNR 的变化范围为0 ～30 dB,噪声为均值为0、方差为σ2h=1 的复高斯随机变量。

图4 和图5 分别给出了多径数为1(平坦衰落)时特征参数d20和识别率(CCR)随SNR 的变化情况。可以看出, d20值与理论计算结果一致;对于2FSK、QPSK、16PSK、64QAM 和128QAM 识别率均可以达到100%;对于OFDM 信号,当SNR 高于5 dB时,识别率可以达到95%以上。

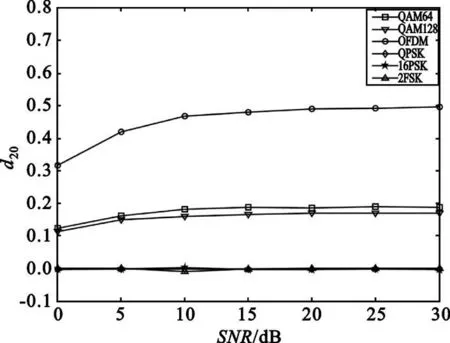
图4 不同调制方式的特征参数d20比较(L=1)Fig.4 d20 of different modulations vs SNR(L=1)

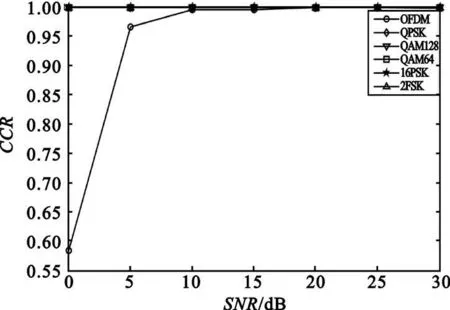
图5 不同调制方式的识别率比较(L=1)Fig.5 CCR of different modulations vs SNR(L=1)

图6 和图7 分别给出了多径数为2 时特征参数d20和CCR 随SNR 的变化情况。可以看出,d20值与理论计算结果一致;此时,由于各种调制方式d20值都较小,因此,识别率有所降低,对于OFDM 信号,当SNR 高于15 dB时,识别率可以达到95%以上。

图6 不同调制方式的特征参数d20比较(L=2)Fig.6 d20 of different modulations vs SNR(L=2)

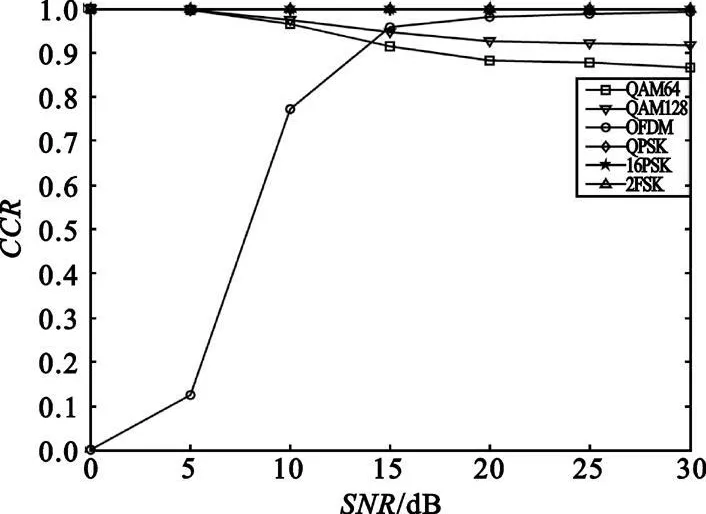
图7 不同调制方式的识别率比较(L=2)Fig.7 CCR of different modulations vs SNR(L=2)

5 结 论

针对频率选择性衰落信道条件下V-BLAST 结构多载波信号盲识别问题,本文提出了一种有效的基于高阶累积量的识别算法,该算法直接从接收的中频信号进行处理,在信道多径数较小时,具有较高的识别率;随着多径数的增加,各种调制方式的特征参数都趋于0,识别率也随之降低。因此,还需进一步研究新的特征参数。

[1] Foschini G J.Layered space-time architecture for wireless communication in a fading environment when using multi-element antennas[ J] .Bell Labs Technical Journal, 1996, 1(2):41-59.

[2] Wolniansky P W, Foschini G J.V-BLAST:an architecture for realizing very high data rates over the rich -scattering wireless channel[C]//Proceedings of 1998 IEEE International Symposium on Signals, Systems, and Electronics.Pisa, Italy:IEEE, 1998:295-300.

[3] Liu Lingjia,Chen Runhua, Stefan G, et al.Downlink MIMO in LTE-Advanced:SU-M IMO vs.MU-MIMO[ J] .IEEE Communications Magazine, 2012, 50(2):140-147.

[4] Dipankar R, Narayan B M.Frontiers of Wireless and Mobile Communications[ J] .Proceedings of the IEEE, 2012, 100(4):824-840.

[5] Gordon L S, John R B, Mclaughlin S W.Broadband MIMO-OFDM Wireless Communications[ J] .Proceedings of the IEEE, 2004, 92(2):271-294.

[6] Yan Wu, Sun Sumei, Lei Zhongding.A Low Complexity VBLAST OFDM Detection Algorithm for Wireless LAN Systems[J] .IEEE Communication Letters,2004,8(6):374-376.

[7] Swam i A, Sadler B M.H ierarchical Digital Modulation Classification Using Cumulants[ J] .IEEE Transactions on Communications, 2000, 48(3):416-429.

[ 8] Nandi A K, Azzouz E E.Algorithms for automatic modulation recognition of communication signals[ J] .IEEE Transactions on Communications, 1998, 46(4):431-436.

[ 9] Mobasseri B B.Digital modulation classification using constellation shape[J] .Signal Processing, 2000, 80(2):251-277.

[ 10] Akmouche W.Detection of mu lticarrier modulations using 4th-order cumulants[ C]// Proceedings of 1999 IEEE Military Communications Conference.Atlantic, USA:IEEE,1999:432-436.

[ 11] Wang Bin, Ge Lindong.A novel algorithm for identification of OFDM signals[C]// Proceedings of 2005 IEEE International Conference on Wireless Communications, Networking and Mobile Computing.Piscataway, USA:IEEE,2005:261-264.

[ 12] Yucek T, Arslan H.A novel sub-optimum maximum likelihood modulation classification algorithm for adaptive OFDM systems[C]// Proceedings of 2004 IEEE Wireless Communications and Networking Conference.Atlanta, USA:IEEE,2004:739-744.

[ 13] Chen Jian, Kuo Yonghong, Liu Xianling.Modulation Identification for MIMO-OFDM Signals[ C]// Proceedings of 2007 IET Conference on W ireless, Mobile and Sensor Networks.Shanghai:IEEE,2007:1013-1016.

[ 14] Proakis J G.Digital communications[M] .4th ed.New York:M cGraw-Hill Press, 2001.