新型文字电话中数字滤波器的设计
唐小容,刘敬浩,宋小璇
(天津大学 电子信息工程学院,天津 300072)
19世纪电话的发明开启了人类通讯的新时代,20世纪文字电话的产生使得聋哑人的远距离实时通信成为了可能,它通过电子屏幕和键盘以聋哑人之间实现实时交流,是一种特殊的电话。传统文字电话高昂的造价局限了它的使用范围,新型文字电话有效地解决了它的这一问题。
文字电话是通过调制解调器将信息调制到指定的语音信号频段上以实现传输,在传输的过程中,通常会受到噪声的干扰。为了保证信息的准确性以及文字电话的实时性,滤波器的设计显得尤为重要。文中采用CSD编码移位相加取代乘法运算可以使计算的次数大为减少,CSD编码与Horner优化多项式算法相结合更能有效的缩短滤波器滤波时间。
1 新型文字电话系统简介
文字电话目前广泛应用于欧美国家,是一种针对特殊人群远程实时通信的解决方案,采用v.21标准、v.23标准等进行调制以实现文字信息在音频线上的传输。
新型文字电话系统首先从键盘读入数据,经v.21标准调制后通过音频线进行传输,在接收部分将从音频线上接收到的数据通过dsPIC33F系列微处理系内部集成的ADC以8kbps的速率采样后,先通过文中所设计的滤波器进行滤波,然后再对接收到的信息进行处理并显示出来。
本系统基于Microchip公司dsPIC33F系列16位数字信号控制器(DSC)来实现。该系列微处理器具有很高的集成度,内置的DSP运算核和DSP指令有很强的数字信号处理能力,其运行速度可达40 MIPS。内部集成了10位和12位两个ADC,其采样速率分别可达到1 100 KSPS和500 KSPS。它的DSP引擎特别适合于数字信号处理,如FFT和数字滤波等。该微处理器依赖于Microchip先进的制造工艺和管理,价格很有竞争力[1],使该系统既能满足文字电话通信的基本要求也大大降低了成本。
2 数字滤波器的设计
数字滤波在数字信号处理中占有非常重要的地位,它可以实现模拟器件很难达到的准确性和相位相关的特性,从20世纪60年代中期开始就出现了各种数字滤波器的逼近方法和实现方法[2]。相对于模拟滤波器,数字滤波器的好处是微功耗、低成本、调整方便、修改容易、设计灵活、没有温度漂移和元件老化等问题。根据冲激响应的时域特性,数字滤波器可以分为无限长冲激响应滤波器(IIR)和有限长冲激响应滤波器(FIR)。FIR滤波器虽然运算量比IIR要大一些,但是FIR滤波器具有线性的相位特性,而且是一个全零点系统,是一个天然的稳定系统。FIR滤波器的突出优点有:系统稳定、易于实现,具有线性相位,允许设计多通带(或多阻带)滤波器,不含反馈环路且结构简单。文中所设计的是FIR滤波器。
FIR滤波器的基本结构可以理解为一个分节的延时线,把每一节的输出加权累加,得到滤波器的输出。FIR的冲激响应h(n)是有限长的,数学上M阶的FIR滤波器可以表示为:
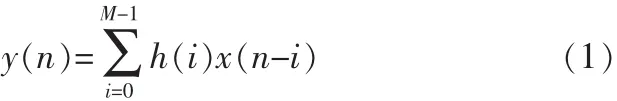
其系统函数为:
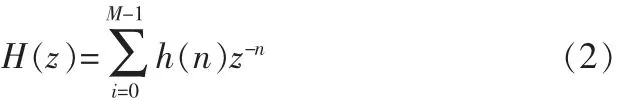
FIR的设计问题实质上是指确定能满足所要求的转移序列或脉冲响应的常数的问题,设计方法主要有窗函数法、频率采样法和等波纹最佳逼近法等。文中借助Momentum Data Systems公司专门为dsPIC设计的数字滤波器辅助设计软件包Filter Design来进行设计。
使用FD软件包可以实现无限冲激响应滤波器 (FIR)的设计,用户可以生成低通、高通、带通和带阻滤波器,最多可支持513个点。它最突出的一个特性是具有代码生成能力,用户可以根据具体要求设计好滤波器后直接生成dsPIC代码,脱离复杂的滤波器手动设计过程[1]。
文中所设计的是一个FIR带通滤波器,在FD的设计界面上输入该滤波器的参数:fs=8 000,fstop1=1 200,fstop2=2 200,fpass1=1 650,fpass2=1 850,Astop1=Astop2=60 dB,Apass=1 dB,设计一个73阶的带通滤波器,其幅频响应以及群延时等如图1所示。

图1 FD设计的带通滤波器Fig.1 Bandpass filter designed by FD
由图1可以看出,所得到的FIR滤波器具有线性相位,通带衰减低于1 dB,阻带衰减大于60 dB,满足设计需要。直接生成dsPIC代码后,发现该滤波器在40MHz晶振条件下,滤波时间过长,影响文字电话系统实时通信,而降低滤波器的阶次,将会影响到滤波器的滤波效果,因此需要对其进行进一步的优化。
3 FIR带通滤波器优化
在数字滤波器、离散傅里叶变换等数字信号处理中,乘法运算是一个最基本的运算,乘法运算的速度决定着数字系统的运算速度。由于新型文字电话对实时性的要求比较高,而在本系统中,dsPIC33F单片机以及晶振40 MHz是固定的,因此为了提高程序运行速度,达到所需要的实时性要求,只能对滤波器系数进行优化,以缩短滤波计算所需要的时间。
在计算机数字表示法中,除常见的2C(二进制补码)等传统的表示法外,还有一些非传统的数字表示法 (如CSD编码),通常可以通过非零元素的数量来估计乘法的效率,因此在一些特定的应用场合或者解决特殊问题时采用这些非传统的数字表示法能提高效率。
正则有符号数CSD编码表示法是一种与传统的二进制编码表示法不同的表示法,它具有三重值,其数字的值域为{0,1,-1},其中-1 常写成1¯,应用 CSD 表示法,可以降低非零元素的数值,在运算中减少加法操作的次数,有利于运算速度的提高。文中依据的是 R.M.M.Oberman提出的CSD基本原理[3],并把它应用于所设计的FIR带通滤波器中。
经典CSD编码表示法的方法是将二进制编码从最低的有效位开始,用10…01¯来取代所有大于或等于2的1序列[3]。这种经典CSD编码的最终表达式在两个非零数位(1,1¯)之间至少有一个0,而且其编码具有唯一性。
基于经典CSD编码可以将式(1),做以下的变化:

由于实际应用时的复杂性,这种经典的CSD编码也不是总能够生成最佳的二进制编码,需要对经典的CSD编码进行修改,变为最佳的CSD编码[4-5],其修改的方法为:
1)从最低有效位开始,用10..01取代所有大于2的1序列;
2)用 1101取代 1011;
3)从最高有效位开始,用011代替101。
修改后得到的最佳CSD编码可以使系数中非零元素的个数减至最少,在[-1,1]内,CSD数相比于二进制补码系统平均减少33%的非零项,这就意味着在实际运算中大大减少了乘法中的乘积项,从而需要更少的加法单元与减法单元。这种编码将在高速乘法器,特别是采用常系数乘法器的滤波器中起到非常重要的作用。
经过最佳CSD编码之后,系数中的非零元素的个数已经减到最少,在多项式的运算中,还有提高运算速度的可能。Horner算法[6]就是一个N次多项式简化算法:

改写成
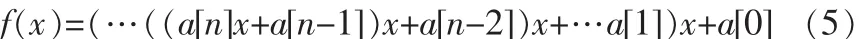
由(5)(6)式可以看到,优化后的多项式可以明显的减少移位的次数。
在实际运算过程中,假设输入为X,输出为Y,而系数为247,其二进制表示为1111 0111,在传统的运算方法下,Y=X*(27+26+25+24+22+21+20),而将其进行CSD编码之后,其码字变为10000-100-1,则输出表达式转变为 Y=X*(28-23-20),进一步采用Horner算法进行多项式优化后变为 Y=X*((25-1)*23-20)。
传统算法与优化之后运算速度的比较如表1所示。

表1 传统算法与优化算法比较Tab.1 Contrast between traditional algorithm and optim ization algortihm
由表1可以得出CSD编码和Horner算法联合使用,减少了运算所需的移位次数以及加法次数,缩短少了运算的所需要时间。
4 FIR带通滤波器在dsPIC33F上实现
文中采用无硬件乘法在dsPIC33F上实现滤波,采用编程的方式直接实现,首先把从Filter Design滤波器设计软件上得到的数据进行截断处理,浮点数运算比较麻烦,将耗费更多的资源和时间,因此本设计将所有的系数左移15位之后取整,这样的量化会带来一些误差,但这些误差都在可以接受的范围之内。
图2反映了该FIR带通滤波器的滤波性能与效果。图2(a)是滤波之前的频谱,可以看到有需要滤除的频率存在;图2(b)则是未经量化之前的设计好的FIR带通滤波器滤波后的结果;图2(c)则是经过量化之后的滤波器滤波后的结果,可以看到量化之后的滤波器效果虽然没有量化之前好,但可以满足系统需要。
最后,把采用传统计算方式实现滤波的程序与采用CSD编码与Horner算法结合后优化算法两段程序进行比较。在程序占用空间上,CSD编码与Horner算法由于还涉及符号等信息,程序段占用空间比传统方法的要大,但文中所涉及的滤波器阶数只有73阶,可以忽略它的影响。而在运行速度上,以在VC++6.0平台上运行作为参考,以处理10 000个采样点的滤波计算为例,传统方式需要423ms,而采用文中介绍的方法之后,仅需235ms,由此可见该方法非常有效。

图2 滤波器系数优化前后滤波效果比较Fig.2 Contrast of filtering effect before and after the optimization of the filter coefficients
5 结束语
文中在用FD软件包设计的FIR带通滤波器的过程中,采用CSD编码与Horner算法相结合的方法对滤波器的系数进行了优化,大大缩短了滤波器的滤波时间,在今后的设计中,为提高滤波器的性能,在系数量化部分可以采用如CSD编码的遗传算法等方法对FIR滤波器系数的CSD编码进行优化设计而不是直接截断处理,这样做会减小由于系数截断或者舍入误差对滤波器性能的影响。该方法提高了新型文字电话系统处理数据的能力,为新型文字电话进一步实现语音数据同传(DSVD)奠定了基础。
[1]石朝林.dsPIC数字信号控制器入门与实战[M].北京:北京航空航天大学出版社,2009.
[2]Parhi K K.A systematic approach for design of digit-serial signal processing architectures[C]//IEEE JSolid-State Circ 1992:29-43.
[3]Oberman RMM.Digital circuits for binary arithmetic[M].London:Macmillan Press Ltd,1979.
[4]张月红,王马华,朱霞.基于FPGA的FIR数字滤波器的优化设计[J].现代电子技术,2011(7):44-46.
ZHANG Yue-hong,WANG Ma-hua,ZHU Xia. Optimal design of FIR digital filter based on FPGA [J].Modern Electronics Technique,2011(7):44-46.
[5]岳颀,蔡远利.基于CSD量化编码的FIR滤波器优化设计[J].西北大学学报:自然科学版,2009(8):541-543.
YUEQi,CAIYuan-li.Canonical signed digit encoding based optimal design for FIR filters[J].Journal of Northwest University:Natural Science Edition,2009(8):541-543.
[6]Abdelgawad,Abdelhak S.A low-powermultiplication algorithm for signal processing in wireless sensor networks[C]//Proc of the 52nd IEEE International Midwest Symposium on Circuits and Systems (MWSCAS’09).Cancun,Canada,2009:695-698.

