基带成形滤波器的数字设计与实现

王顶，刘智朋，赵颐轩

（西北工业大学 电子信息学院，陕西 西安 710129）

在现代无线电通信中，由于基带信号的频谱范围都比较宽，为了有效利用信道，在信号传输出去之前，都要对信号进行频谱压缩，使其在消除码间干扰和达到最佳检测的前提下，大大提高频谱利用率[1]。为此，在数字基带传输系统中，压缩基带信号频谱的主要方法就是采用基带成型滤波器。而伴随着超高速数字集成电路的发展，成型滤波器已经由过去的基带频域模拟成型滤波器变成现在的基带时域数字成型滤波器。与基带模拟成型滤波器相比，基带数字成型滤波器具有高精度、高可靠性和高灵活性等优点；同时还便于大规模集成、易于实现线性相位等特点[2]。实现数字基带成型的方法有很多，如抽头延迟线模型（FIR）、格型滤波器及级联型（IIR）等，文中采用基于FPGA的查表操作来实现数字基带成型滤波器的功能，查表法是预先将信号所有可能的成型后的基带波形的样本值存储起来，根据输入数据序列，从存储器中查找并输出对应的波形，这种方法简单、直观、速度快。

1 基带成型滤波器原理

由奈奎斯特第一准则可知：如果信号经传输后整个波形发生了变化，但只要其特定点的抽样值保持不变，那么用再次抽样的方法，仍然可以准确无误的恢复原始信码[3]。为了说明基带成型滤波器的基本原理，先将基带传输系统的模型构建如图1所示[4]。

图1 基带传输系统模型Fig．1 Baseband transmission system model

若要实现无码间干扰的基带传输，则该系统总的传输特性应该满足下式[5]：

但该式所表达出来的特性是理想的，是无法实现的，而且即使获得了相当逼近理想的特性，把理想的冲激响应h（t）作为传输波形仍然是不适宜的。这是因为，波形h（t）的“尾巴”衰减振荡幅度较大，因此在得不到严格定时时，码间干扰就可能达到很大的数值。

从实际的滤波器的实现和对定时的要求等方面考虑，采用具有升余弦频谱特性的H（w）比较合适，其所对应的冲激响应 h（t）为下式[6]：

其中 α 为滚降系数，且 0≤α≤1，Ts为码元周期。 h（t）的时域波形如图2所示[7]。

图2 冲激响应Fig．2 Impulse response

由图2可以看出，升余弦信号在前后抽样值处（间隔Ts）的串扰始终为零，满足奈奎斯特第一准则，可以消除码间干扰（ISI）。

设{x（t）}为成型滤波器的输入码元序列，可将其表示为：

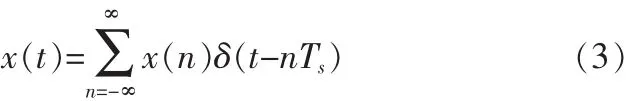
其中 x（n）的取值为-1、+1。

当该输入码元序列经过冲激响应为h（t）的成型滤波器时，所对应的输出响应为下式[8]：

2 基带成型滤波器的MATLAB设计

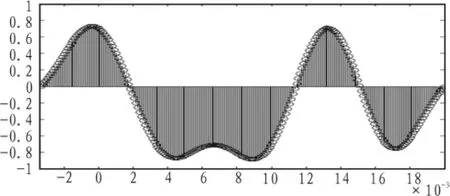
图3 输入100010时的输出序列波形Fig．3 The output sequencewaveform when enter 100010

输入码元序列总共有n=2L=64种情况，则对应的基带成型后的输出序列波形所需要的采样总点数为：L×n×32=12 288，若每个点采用8 bit的量化，则得到数据存储量为12 k字节。

在实际的硬件电路实现过程中，让输入码元序列串行移入移位寄存器，也就是说每次向移位寄存器中移入1个码元，然后再通过查表操作得到该输入码元成型后的序列波形，所以直观上来看，对于每种输入序列所对应的192个输出序列波形点，只需要取其最后32个点进行存储即可，那么其总的数据存储量只有2k字节。

由于输入码元所对应的成型后的序列波形走向会受到下一个输入码元的影响，也就是说在不知道下一个输入码元时，该输入码元成型后的序列波形就会存在两种情况。假设移位寄存器中的初始状态为“000000”，当输入码元“1”时，移位寄存器里面的状态变为“000001”，则在不知道下一输入码元的情况下，该输入码元所对应的成型后的序列波形如图4所示。

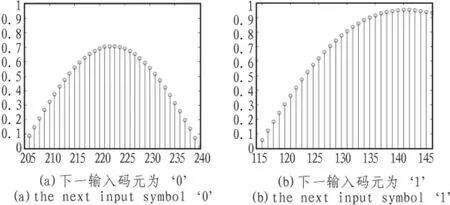
图4 输入码元‘1’在不同的下一输入码元时所对应的成型后波形Fig．4 Moldingwaveform when entering code ‘1’ in different next input code

由上图可知，对于输入码元“1”来说，当下一个码元输入为“0”时，其成型后的波形走向是趋于 0的，如图4（a）所示；当下一个输入码元为“1”时，其成型后的波形走向趋于平坦，如图 4（b）所示。

由于通过MATLAB仿真出来的192点输出序列波形的后32个点的走向总是趋向于0的，考虑到前面所述情况，若将其存储制作成表，则会得出错误的成型结果。因此，应该将每种输出序列的第129点到160点（共32点）取出来，进行存储制作成表，就可以解决前面所述的问题。

3 基带成型滤波器的FPGA实现

由于FPGA器件具有速度快、密度高、功耗低、可配置性强等优良特性，因此，在此设计中选用Xilinx公司的Spartan3 XC3S200 FPGA芯片来搭建硬件系统平台，该芯片内置了216 k的Block RAM，完全足够存储输出数据。

将输入信号以Ts为周期，按每次1 bit串行放入一个长度为6 bit的移位寄存器，然后以该6 bit的数据作为高位地址，后面再缀上5 bit的低位地址，当低5位的地址从”00000”变化到”11111”时，就以查表寻址的方式在存储器中找到了输入信号在基带成型滤波后的波形数值。查表寻址方式的原理框图如图5所示。

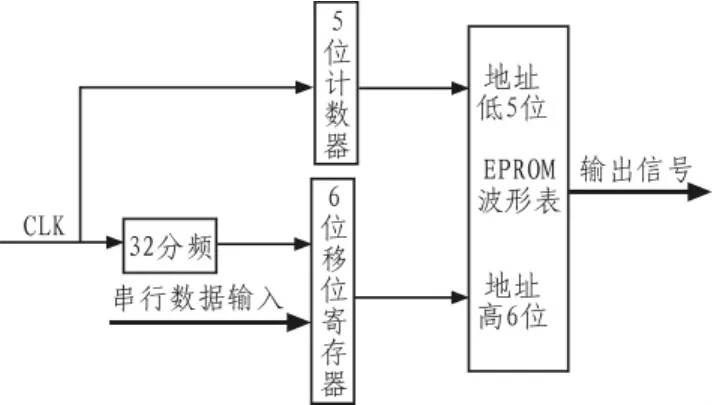
图5 查表寻址方式原理框图Fig．5 Look-up table addressing block diagram

但需要注意的是，由于在MATLAB程序中，对于每种输出波形序列，只是将采样得到的第129点到160点取出来进行存储的，所以在t时刻所得到的基带成型后的波形数值，所对应的信号应该是t-Ts时刻输入的。

当串行输入数据为 “0000 1010 0101 0111 0101 1110 0001”时，经过查表寻址，用 MODELSIM6．0仿真出来的结果如图6所示。

由图6可以看出，在各个取样点码之间的串扰比较小，达到了基带信号成型的目的。

图6 仿真结果Fig．6 Simulation results

4 结束语

文中着重研究了现代通信系统中基带成型滤波器的数字设计与实现方法，该方法基于FPGA的查表操作来实现，占用系统资源相对于传统方法有很大的降低，并且试验结果表明所设计实现的成型滤波器可以很好地完成通信系统中基带信号的成型特性。

[1]王建新，蒋立平，吉训生，等．基带成型滤波器的FPGA实现[J]．电讯技术，2001（5）：43-46．

WANG Jian-xin，JIANG Li-ping，JIXun-sheng，et al．Baseband formation filter FPGA realizes[J]．Telecommunication Technology，2001（5）：43-46．

[2]马娅娜，杜栓义，陈立娜．16QAM基带成型滤波器[J]．现代电子技术，2007（4）：18-20．

MA Ya-na，DU Shuan-yi，CHEN Li-na．16QAM baseband formation filter[J]．Modern Electronic Technology，2007 （4）：18-20．

[3]田耘，徐文波，张延伟，等．无线通信FPGA设计[M]．北京：电子工业出版社，2008．

[4]易波．现代通信导论[M]．长沙：国防科学技术大学出版社，1998．

[5]樊昌信，张甫翊，徐炳祥，等．通信原理[M]．5版．北京：国防工业出版社，2001．

[6]陈东华．升余弦滚降基带成型内插滤波器的FPGA实现[J]．华侨大学学报：自然科学版，2006（3）：92-94．

CHEN Dong-hua．Implementato of raised-cosine roll-off pulse shaping interpolated filter based on FPGA[J]．Journal of Huaqiao University：NaturalSciencesVersion，2006（3）：92-94．

[7]胡爱群，苏杰，庞康．基带成型滤波器的数字实现[J]．数据采集与处理，1996（1）：53-55．

HU Ai-qun，SU Jie，PANG Kang．The baseband formation filter numeral realizes the[J]．Data Acquisition and Processes，1996（1）：53-55．

[8]邓涛．卫星数据采集系统远端站基带型号处理 [D]．上海：华东师范大学，2005．

[9]King MS，Chung JG．Look-up table based pulse-shaping filter[J]．Electronics Letters，2000，36（17）：1505-1507．