自适应稀疏约束图像超分辨力重建方法
干宗良,粱秀聚
(南京邮电大学 通信与信息工程学院,江苏 南京 210003)
在图像采集处理中,为了提高图像的分辨力,最直接的办法是提高硬件设备的采集能力或图像增强技术[1-2]。但这种方式不仅成本高,还受到物理极限的限制。超分辨力重建是一种基于信号处理理论的软件技术,能在不改变硬件设备的情况下有效地提高图像分辨力,增加细节和信息[3-4]。它已成为图像处理领域的一个研究热点。现有的超分辨力重建技术可分为两类:基于约束集的算法和学习算法。基于约束集的算法就是对图像获取过程中的降质过程建立先验模型,通过求解模型的逆问题来重建高分辨力图像(例如反向迭代投影算法[5],双边滤波反向投影算法[6])。然而,要达到较好的效果,这类方法不仅需要解决一个图像亚像素的对齐问题,同时还受到放大倍数的制约。因此,这种传统的基于约束集的算法继续发展的潜力有限。学习算法被认为是很有潜力的超分辨力重建算法,得到了很多学者的关注[7-10]。它是通过学习高低分辨力图像块之间的关系,指导图像的高频信息重建。
基于图像稀疏冗余模型的算法,通过学习训练集中低分辨力图像与相应的高分辨力图像之间的关系,利用这种关系来指导其他图像的超分辨力重建,在放大倍数较大时仍有较好的重建效果。Jianchao Yang等在2008年提出了基于稀疏描述的图像超分辨力重建技术[9],此算法基于压缩感知理论,信号的稀疏描述可由其下采样后的信号精确恢复。在解决图像超分辨力重建问题中可描述为:高分辨力图像块的稀疏表示系数可由相应的低分辨力图像块精确恢复。在建立一个合适的过完备图像块库后,计算出输入的低分辨力图像块的稀疏线性表示系数,然后利用这些系数结合高分辨力图像库,重建相应的高分辨力图像块。基于稀疏描述方法的缺点是计算复杂度较大。Jianchao Yang等在2010年又对此方法做出了改进,加入了字典训练过程,并且为确保高、低分辨力图像块表示系数的一致性,对采集到的高、低分辨力图像块进行联合训练[10]。相比之前直接利用原图像块集,此方法获得的字典更紧致,在很大程度上降低了重建的计算复杂度。
在实际应用中,评价一个图像超分辨力重建算法的好坏,除比较其重建图像的主客观质量外,还要考虑其重建的时间消耗。基于稀疏约束的算法在重建时需要对每个小图像块进行稀疏线性表示系数的计算,其计算复杂度较高。并针对其计算复杂度高的问题,本文提出了一种基于K均值聚类的自适应快速重建方法。所提算法从两个方面降低其计算复杂度:1)分类训练字典,对图像块归类重建,降低每个图像块所用字典的大小;2)对图像块的特征进行分析,自适应地选择重建方法。实验结果表明,本文提出的快速重建方法在重建质量与原算法相当的前提下,可以较大程度地降低重建时间。
1 基于稀疏约束的超分辨力重建算法[8]
稀疏约束是假定高分辨力图像块能由一个合适的过完备字典中的原子稀疏线性表示,且其表示系数能由相对应的低分辨力图像块获得

式中:x为高分辨力图像X中的某图像块,为一维向量;Dh为由训练集中高分辨力图像块训练得到的字典;a为稀疏表示系数,为一维向量,可由输入的低分辨力图像Y中相应的图像块y,结合低分辨力图像块字典Dl获得,其中要求字典Dh与Dl通过联合训练获得。式(1)是一个NP难问题,可以通过松弛算法,将L0范数问题转换为L1范数问题。
对于输入的低分辨力图像块y,其稀疏表示系数a可由式(2)获得
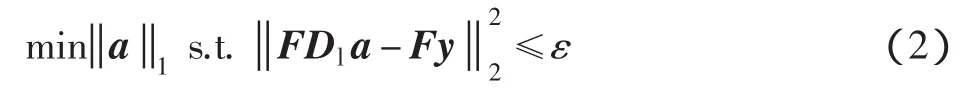
式中:F是一个特征值提取操作符,用于提取标识本图像块的特征。式(2)还可由拉格朗日乘子转换为一个等价的公式
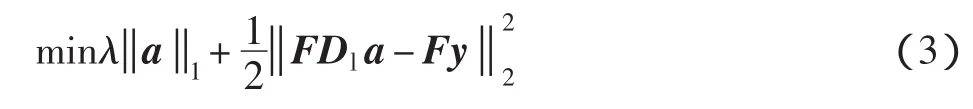
式中:参数λ用来平衡解的稀疏度与低分辨力图像块Y的重建误差。为实现相邻图像块之间的兼容,需要在对图像分块处理时进行一定的重叠,则上述最优化问题可转化为
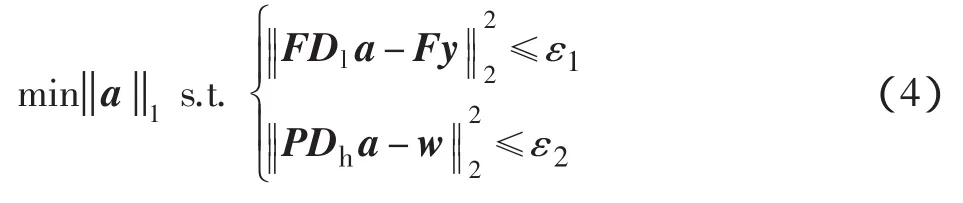
式中:矩阵P提取当前重建块中与已重建部分的重叠像素;w是重叠区域的已重建的像素。
式(4)同样可由拉格朗日乘子转换为一个等价的公式

通过上式求出最优解a*后,结合相应的高分辨力字典Dh,即可重建出高分辨力图像块

2 基于K均值聚类的自适应稀疏描述的快速超分辨力重建方法
2.1 问题描述
首先建一个高、低分辨力图像块样本库,训练成大小分别为250,500,1 000,2 000,4 000的字典,然后对同一幅图像进行重建,记录其重建消耗的时间。图1是对两幅大小不同的图像重建消耗的时间进行统计的结果。
从图1中可以看出,重建消耗的时间与字典的大小近似成线性关系,因此,有效地降低字典的大小能降低重建消耗的时间。而对样本图像块分类可以有效地降低字典的大小。
在不影响重建效果的前提下,可以用计算复杂度低的算法取代高复杂度的算法。对图像进行分块,分别比较双立方插值与基于稀疏约束模型的重建算法的重建效果,如图2所示。其中,白色的点标识代表基于稀疏约束的算法优于双立方插值算法,黑色的点标识代表两个重建效果相差不大,以PSNR值为衡量标准。
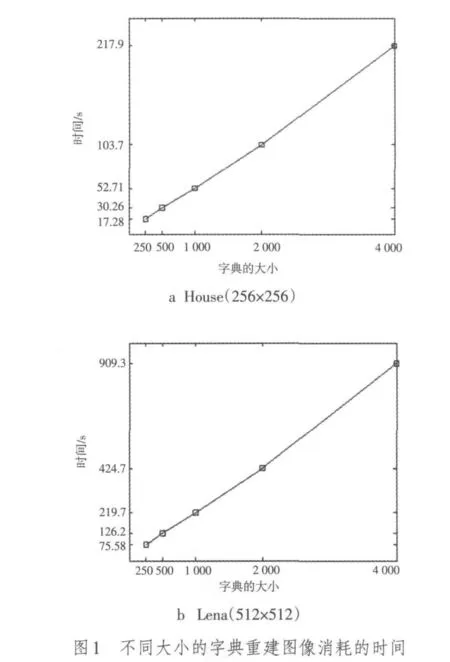
图1 不同大小的字典重建图像消耗的时间
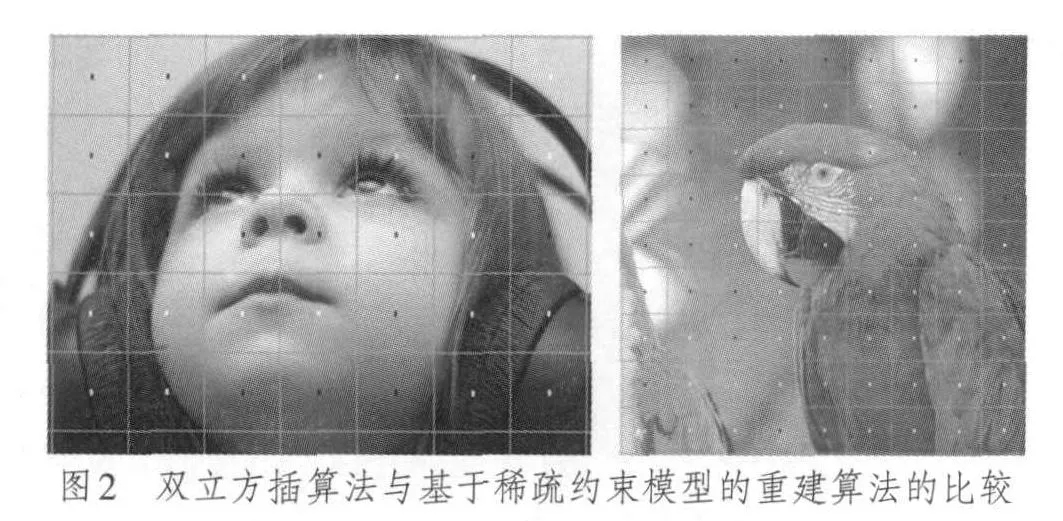
图2 双立方插算法与基于稀疏约束模型的重建算法的比较
从图2中可以看出,在图像的平滑区域,两种算法的重建效果相差不大,可以用复杂度低的双立方插值算法取代基于稀疏约束模型的重建算法。因此,在重建过程中,可以根据图像块的特征自适应地选择重建方法,降低算法的计算复杂度。
2.2 算法描述
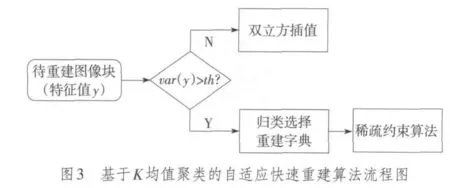
综上所述,本文的算法框图如图3所示。针对一个待重建的图像块:1)首先判断图像块的方差,如果小于预定门限,则直接进行双立方内插,如果大于门限,则进行基于稀疏字典约束的SR重建;2)对于需要进行基于稀疏字典约束的SR重建的图像块,根据分类结果,选择合适的字典库,进行相应稀疏约束的重建,如式(5)。
2.2.1 基于K均值聚类的字典库训练
在字典训练阶段,先利用K-Means聚类算法[9]对样本图像块进行分类。然后,对每个聚类的图像块单独进行字典训练,生成K个子字典。其与原训练字典方法的区别如图4所示,图4b中要求K个聚类子字典大小之和等于未分类字典D的大小。
在图像的重建过程中,首先对图像进行分块,然后对每个待重建的图像块进行归类,选择其所属聚类的字典进行重建。其中,对图像块的归类方法是:计算此图像块的特征向量与K个聚类的中心点的欧氏距离,比较K个距离的大小,将其归为距离最小的聚类,如式(7)及式(8)所示


图4 字典训练流程图
式中:y表示图像块的特征向量;ci表示第i聚类的中心点。
本文将样本图像块分为8类,图5是分类前后高分辨力图像块的字典。其中,原字典展示的是前80个原子,而分类字典展示的是每一类的前10个原子。

选择5个图像块用上述两个字典进行重建时的稀疏表示原子进行了跟踪,如图6所示。其中,图6a是低分辨力图像块特征放大3倍的结果,图6b及图6c分别是原字典及分类后的字典中用来稀疏线性表示相应低分辨力图像块的原子,图中只显示了稀疏表示系数较大的前5个原子。

从图6可以看出,对一个低分辨力图像块,在分类后的子字典中找到的稀疏线性表示原子与在原字典中找到的原子的纹理相近,从而可以确保使用分类的子字典进行图像重建的效果。
2.2.2 自适应内容的超分辨力重建
对图像分块后,先计算每块图像的方差,然后根据方差大小自适应地选择重建方法。如果小于设定的门限值,则利用双立方插值进行重建。
在具体实现过程中,由于不同的算法重建的图像是有一定区别的,对图像块使用不同的重建算法具有一定的拼接效应。因此,需要加入局部重建约束,平滑两种算法的结合处。
局部重建约束是通过加强基于稀疏约束算法重建的图像块与双立方算法重建结果的相似性,降低重建图像的拼接效应,其约束条件为

式中:xSR与xBic分别表示基于稀疏约束重建图像块的特征向量与双立方算法重建的图像块特征向量;γ为常量。
3 实验结果
在仿真实验中,基于K均值聚类的算法与原算法使用相同的图像训练集。图7是实验所使用的图像训练集,图8是实验所使用的测试图像。与原未分类的算法进行两方面的比较:1)重建消耗的时间;2)重建图像的主客观质量。对于原算法,从图像训练集中选取20 000个高、低分辨力图像块对,然后将其训练成大小为2 000的字典,其中低分辨力图像块大小为3×3,高分辨力图像块大小为9×9。对于K均值聚类的算法,在从图像训练集中选取样本图像块对后,首先要利用K-Means聚类算法对其分类,本文共分为8类;然后,分别对此8类样本图像块进行字典训练,其中每类子字典的大小与其所对应的样本库的大小成正比,所有子字典大小之和为2 000。重建均采用全局约束方式。
对图8a~图8f这6幅图像进行了测试。首先,将原始高分辨图像进行高斯滤波模糊、3倍下采样;然后,将降质后的图像用此两种算法进行重建。其中,降质过程所用的高斯核函数的窗口为5,方差为1。并且在实验中只对彩色图像的亮度通道进行重建,而对色差信号只进行简单的双立方插值处理。在重建过程中,两种算法的重建参数设置完全相同。相邻块之间的重叠为2,放大倍数为3,全局约束采用迭代反投影算法。
1)重建时间的比较
本文提出的算法的计算复杂度与图像的纹理特征相关,重建效率的提高程度因图而异,下面列出了6幅大小不同的图像的测试结果作为参考,见表1。其中,SR算法代表原始算法,两种算法在相同的测试环境下运行。从表1中可以看出本文提出的算法在很大程度上缩短了重建时间,平均缩短7倍左右。

表1 两种算法重建时间的比较
2)重建效果的比较
实验分别从主观及客观两个方面进行重建质量的比较,表2中列出了3幅图像的重建客观质量,以PSNR及FSIM[10]为衡量标准,并且加入了双立方插值算法的结果作为参考,其中SR_glb算法及本文算法均加入了全局重建约束,两种算法采用相同的全局后处理方法。从表中可以看出,本文提出的快速重建算法在客观重建质量上与原算法相当。

表2 不同算法的客观重建质量
为给出较清晰的主观视觉的比较,实验截取了3幅测试图像的重建结果,如图9~图11所示。从图中可以看出,与双立方插值算法相比,基于稀疏约束模型重建的图像纹理细节较清晰,且本文提出的快速重建方法保留了原算法的优势,在主观视觉上与原算法相当。



从以上两个方面的比较可以得出,本文提出的基于K均值聚类的自适应快速重建方法可在保证重建主、客观质量与原算法相当的前提下,降低基于稀疏约束模型算法的计算复杂度,从而可以缩短图像超分辨力重建消耗的时间。
4 结论
本文首先简要介绍了基于稀疏约束的算法,并针对其计算复杂度高的问题,提出了一种基于K均值聚类的自适应快速重建方法。所提算法从两个方面降低其计算复杂度:1)分类训练字典,对图像块归类重建,降低每个图像块所用字典的大小;2)对图像块的特征进行分析,自适应地选择重建方法。实验结果表明,本文提出的快速重建方法在重建质量与原算法相当的前提下,可以较大程度地降低重建时间。
[1]任炎辉,李仅伟,毕卫红.一种优化参数的图像增强算法[J].电视技术,2012,36(3):7-10.
[2]俞志峰,张乐,江浩,等.一种提升电视图像质量的自适应去隔行算法[J].电视技术,2010,34(S1):73-75.
[3]PARK S C,PARK M K,KANG M G.Super-resolution image reconstruction:a technical review[J].IEEE Signal Processing Magazine,2003,5(21):21-36.
[4]FARSIU S,ROBINSON M D,ELAD M.Fast and robust multiframe super resolution[J].IEEE Trans.Image Processing,2004,13(10):1327-1344.
[3]IRANI M,PELEG S.Motion analysis for image enhancement:resolution,occlusion and transparency[J].Journal of Visual Communication and Image Representation,1993,4(4):324-355.
[4]DAI Shengyang,HAN Mei,WU Ying,et al.Bilateral back-projection for single image super resolution[C]//Proc.IEEE Conference on Multimedia and Expo,2007.[S.l.]:IEEE Press,2007:1039-1042.
[5]FREEMAN W T,JONES T R,PASZTOR E C.Example-based super-resolution[J].IEEE Computer Graphics and Applications,2002,22(2):56-65.
[6]CHANG Hong,YEUNG D Y,XIONG Yimin.Super-resolution through neighbor embedding[C]//Proc.IEEE conference on CVPR.[S.l.]:IEEE Press,2004:275-282.
[7]YANG Jianchao,WRIGHT J,HUANG T,et al.Image super-resolution as sparse representation of raw image patches[C]//Proc.IEEE conference on CVPR.[S.l.]:IEEE Press,2008:1-8.
[8]YANG Jianchao,WRIGHT J,HUANG T,et al.Image super-resolution via sparse representation[J].IEEE Trans.Image Processing,2010,19(11):2861-2873.
[9]DAVID J C M.Information theory,inference and learning algorithms[M].[S.l.]:Cambridge University Press,2003:284-292.
[10]ZHANG Lin,ZHANG Lei,MOU X,et al.FSIM:A feature similarity index for image quality assessment[J].IEEE Trans.Image Processing,2011,20(8):2378-2386.

