网络安全与执法专业离散数学课程教学改革探索
王 慧, 王斌君
(中国人民公安大学信息安全工程系,北京 100038)
0 引言
随着社会信息化的进一步深入,网络犯罪的发案率逐年急剧上升,为适应新形势下公安工作的需要,网络安全与执法作为一新兴公安专业,旨在培养与计算机网络犯罪相关的应用型公安高级专门技术人才,在公安机关网络保卫执法部门及相关领域从事预防网络犯罪、控制网络犯罪和处置网络犯罪的工作。坚实的计算机基础知识、软件开发技术、网络情报技术、计算机犯罪侦查取证技术和网络监察技术是该专业的必须。
离散数学作为计算机相关专业的通修课,其主要内容包括数理逻辑、集合与关系、代数结构与布尔代数、图论及有限推理与自动机五部分[1],所研究的是离散对象的数据特点、数据表达方式、相互关系及数学分析方法等内容[2]。该课程具有概念多、高度抽象、各章节之间逻辑联系紧密、推理证明过程特殊等特点,一直是学生比较难于理解和掌握的课程。
网络安全与执法专业虽然属于计算机相关专业,但是与纯粹计算机科学与技术专业相比,其针对性应用性较强。离散数学作为该专业的专业基础课,教学过程需要突出实用性,教学内容与教学方法的选择需体现专业特色,结合知识模块及专业特点进行特色教学,充分培养学生学习自信、激发学习兴趣、提高学习能力、拓展应用水平。
1 离散数学在网络安全与执法专业课程体系中的地位
离散数学是一门专业基础课,但有别于高等数学等基础数学学科,具有明显的专业特征,在网络安全与执法专业的整个课程体系中与后续专业课程的教学有着极其紧密的联系,教学内容主要包括数理逻辑、集合与关系、代数系统及图论四部分,有限推理与自动机理论不在大纲要求的范围之内,其每一部分内容都关联着若干专业课的教学,如图1所示。

图1 离散数学与专业课程间的关系
从图1可以看出,离散数学课程具有典型的专业基础特点,支撑着多门专业课程,学生对该课程的掌握程度直接影响着所承接专业课程的教学效果。
除此之外,离散数学又是应用广泛的数学手段。数理逻辑在数学建模、计算机语义分析中的应用;集合与关系在粗糙集属性约简、数据挖掘过程中的应用;代数系统在信息安全密码分析中的应用;图论在信息查询与检索、指令优化中的应用;都突出显示了离散数学的数学工具特征。
总之,离散数学知识渗透在网络与计算机相关技术的各个方面,在网络安全与执法专业的整个课程体系中占有突出重要的地位,如何提升教学效果对于该专业本科教学乃至研究生培养都具有突出意义。
2 离散数学的知识体系
根据网络安全与执法专业的本科培养方案,离散数学的讲授内容具体包括命题逻辑、一阶逻辑、集合论、关系与函数、代数结构及图论六部分,其中前一部分内容是后一部分必要的前接,后一部分是前面内容的进一步扩展,为改善离散数学课程的课堂教学效果,首先需要为学生理清知识体系内各个模块之间的递进关系,各模块间关系如图2所示。
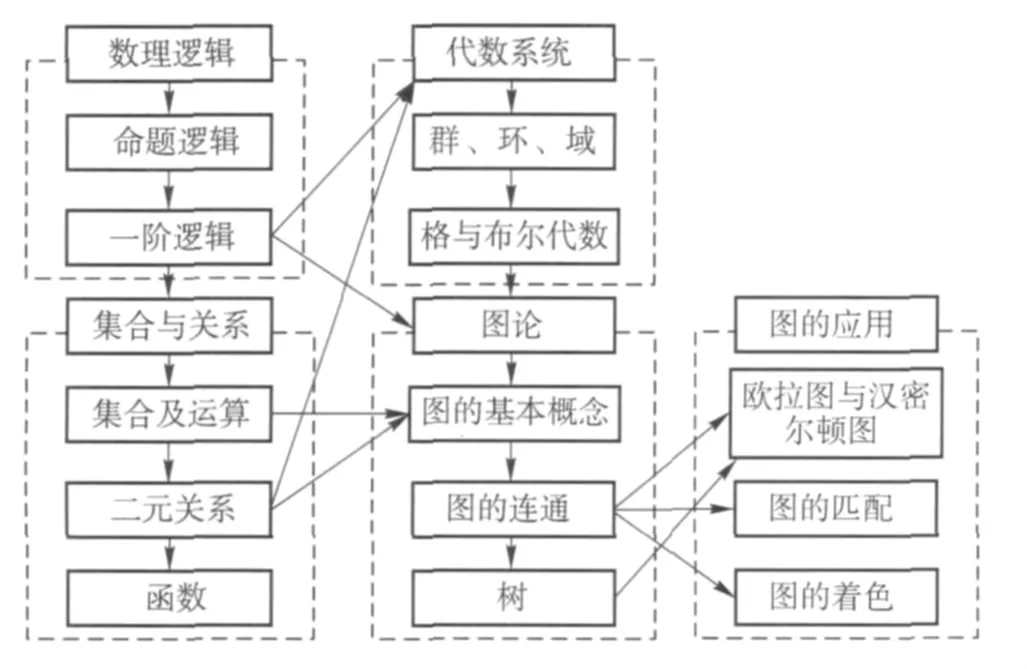
图2 教学模块间的衔接关系图
离散数学的知识体系逻辑性与抽象性强[3],各教学模块间层层关联,任何一部分的学习都无法摆脱前序内容的基础性铺垫,模块间层层递进,是该课程最突出的特点,因此实际教学过程中讲述清楚该课程的知识体系及各教学模块的特点有利于学生对该课程的理解及掌握。
3 教学模式改革
在了解离散数学的专业地位及知识体系特点的基础上,教学过程中需要向学生充分强调学习该课程的必要性,同时结合各教学模块的特点进行特色教学,注重培养学生的抽象概括能力、逻辑推理判断能力及严谨的治学态度,同时结合教学案例及实验设计激发学生的学习兴趣。主要从以下几方面结合教学内容进行教学模式的改革。
1)引入案例教学,激发学习兴趣
在整个知识体系中,数理逻辑、关系、图论教学模块中相关知识的实际应用性较强,因此在学生了解并掌握一定基础知识之后,适当引入趣味性较强的案例展开讨论,既可对知识点、计算方法进行扩展,又可以加深对知识点、方法的理解。
如在命题逻辑中,主范式的求取及判定是等价式的证明、推理有效性证明的方法之一。熟练掌握范式的概念及计算过程有助于推理过程、等价关系的算法设计。授课过程中可以通过下述案例渗透范式的相关知识,也可以通过该例题引入范式的概念,培养学生探索知识的兴趣。
例:在某个案件审理过程中存在四个犯罪嫌疑人,分别为甲、乙、丙、丁,针对某一既定事实,四人只是分别作如下简单回答:甲说:“不是我”,乙说:“是丁”,丙说:“是乙”,丁说:“不是我”,通过排查确知四人回答只有一人符合实际,问可能的嫌疑人是谁?
可以通过如下方式进行推论:
第一步:假设阶段,设P:事件甲参与,Q:事件乙参与,R:事件丙参与,S:事件丁参与
第二步:依据四人回答只有一人符合实际的情况,列出如下公式:
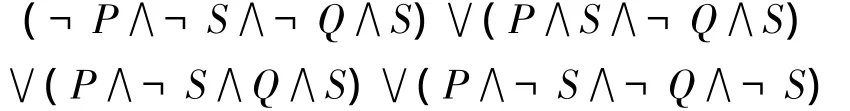
第三步:求上式的主析取范式得出可能情况的组合,主析取范式为:

第四步:对上式进行分析,得出结论。
最可能的犯罪组合只能是:甲、丙、丁或甲、丁或甲、丙,若只有一人参与事件,则参与人是甲。针对上述分析,可以确认重点人物是甲。
上述例题也可以进一步扩展到范式求取的算法设计,以强化数学模型与软件设计间的关系。
在其他模块的讲授中也可以有针对性设计应用型案例辅助教学,如命题逻辑基础知识可以进行硬件电路设计,关系模块中偏序关系可以设计涉案证据链的梳理,图论中图的着色问题可以设计涉案地点的串并分析等。
总之,案例教学的引入既有助于学生自主学习能力的培养,又有助于实际问题的客观抽象形成数学模型以及依据数学模型设计软件解决问题的学术思维习惯的培养。
2)注重习题讨论,鼓励一题多解
离散数学既是计算机相关专业的基础课程,又是一门数学课程,具有典型的数学特色,习题讲授是整个教学中的关键环节。就教学而言,知识点高级应用在于实际问题的综合处理,习题仅仅是知识点的初级应用,但习题却是重要的基础环节,通过习题课的纵向串联,可以加深学生对相关知识点的掌握,同时习题课中可以鼓励学生参与讨论,从不同侧面提出解题方案,进一步理解知识的精髓。
离散数学授课内容中最典型的一题多解实例是命题逻辑中推理有效的证明,其证明过程可以通过真值表、等值演算、主范式、蕴涵式的证明、自然推理系统中的构造法及归谬法、归结推理等手段进行,一个典型例题的讲述可以将命题逻辑中80%的知识点进行回顾性纵向分析。因此在习题课上适当引导学生从不同角度不同层次进行讨论分析,使学生在讨论中发现不同方法在不同类型问题解决过程中的优劣所在,将有助于学生自身知识体系的形成。其他知识点的讲授过程中适当增加针对性习题讨论也同样会取得事半功倍的效果。
3)设计实验环节,强化动手能力
离散数学是一门高度抽象、高度概括、逻辑理论性强的课程,学生通常都难以理解。若在教学过程中适当引入部分实验项目,既可以进行基本理论的具体验证,又可以为专业课的教学打下基础,同时培养学生的动手能力及创新能力[4]。

表1 辅助实验内容
结合网络安全与执法专业的培养方向,根据教学内容中的知识点可以设计不同的实验内容,具体实验开发平台可以使用学生容易掌握的Matlab或C语言,实验项目也可以通过大作业的形式在课下通过分组讨论合作完成。部分实验设计内容如表1所示。
实验教学的引入可以避免学生将离散数学课程作为一门纯粹的数学课对待,适当的程序设计可以使学生将抽象的知识具体化,有利于教学内容的深入掌握。
4)渗透前沿算法,拓展知识结构
目前,许多算法都与离散数学中的知识点相关,如粗糙集属性约简理论的基础是不可区分关系,而不可区分关系本身就是等价关系,经典的基于正区域的属性约简过程在等价划分构造的基础上进行;凯撒密码的本质即群理论;欧拉定理及费马小定理是RSA密码体系的数学基础;群优化算法中蚁群算法的基本模型即采用组合优化算法解决图论中汉密尔顿回路问题;概念格是偏序关系与格结构的体现,其上的关联规则挖掘算法简单直观。在教学过程将知识点进行适当延伸,可以扩展学生的知识结构,了解网络及计算机整个学科建设的前沿,坚定对专业学习的信心。
4 结论
网络安全与执法专业的离散数学教学既要突出其作为专业基础课的专业特点,又要侧重于数学知识点的应用,适当弱化基础性原理与定理的证明,结合专业特色整合教学内容,辅之以实验及各种交互教学模式,可以有效提高学生的逻辑思维判断能力及分析解决实际问题的能力,对于该专业整个课程体系的建设具有重要意义。
[1]左孝凌.离散数学的形成、发展及其在计算机科学中的作用与地位[J].自然杂志.1984,7(6):414-417.
[2]耿素云,曲婉玲.离散数学[M].北京:高等教育出版社,2010.
[3]王霞,顾勋梅,潘祝山.离散数学教学改革与课程建设研究[J].计算机教育,2011(6):8-10.
[4]谭作文.离散数学课程中实验教学探讨[J].计算机教育,2010(17):106-109.

