超混沌Lü系统的反同步研究

高智中



超混沌Lü系统的反同步研究

高智中

（安徽科技学院理学院，安徽，凤阳 233100）

针对超混沌Lü系统，解析地设计了非线性控制器，基于线性系统稳定性定理，实现了超混沌Lü系统的反同步和异结构反同步，给出了理论分析和数值模拟结果。结果表明所设计的非线性控制器能够有效地使两系统达到反同步。

超混沌Lü系统；非线性控制器；线性系统稳定性定理；反同

混沌同步是对混沌系统施加控制使系统的轨道与另一混沌系统或另一演化规律相同但初值不同的同类混沌系统的轨道渐近地趋向一致，它是自然界的一种常见的现象[1]。反同步是两个混沌系统的状态变量的绝对值相同但符号相反，也就是状态变量的和为零的同步现象。1990年，Pecora和Corroll[2]首次提出混沌同步的原理，并在电路实验中成功地实现了混沌同步，近年来混沌同步得到了广泛而深入的研究。比如文献[3-4]设计了不同的非线性反馈控制器实现了四维超混沌系统的自同步，文献[5-6]分别研究了两个耦合的分数阶Chen系统的混沌投影同步控制和统一混沌系统的同步控制，文献[7-10]针对不同系统研究了混沌系统的反同步。从现有文献和实际工程应用来看，混沌反同步比混沌同步更具抗破译能力，混沌反同步在保密通信中可以拓展数字编码方式，产生更多保密通信的设计方案，且有较好的保密性，同时与低维混沌系统相比超混沌系统具有更复杂的动力学行为，因此超混沌系统的自反同步和异结构反同步具有更高的应用价值和更广阔的发展前景。

本文在现有文献基础上，针对文献[11]报道的一个超混沌Lü系统，解析地设计了非线性控制器，基于线性系统稳定性定理，研究了该系统的自反同步和异结构反同步。

1 超混沌Lü系统描述

超混沌Lü系统的数学模型为

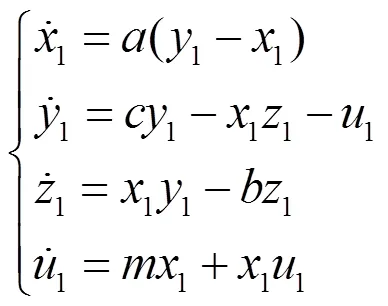
2 超混沌Lü系统反同步

2.1 系统自反同步

设系统(1)为驱动系统，取如下的系统(2)为响应系统

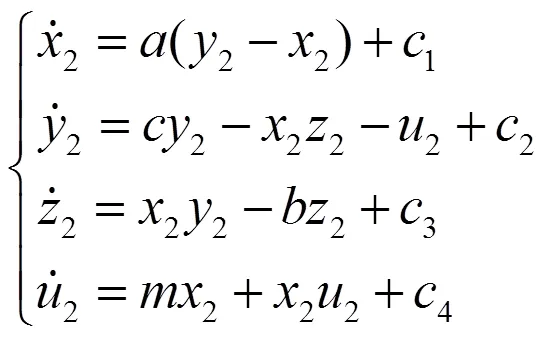
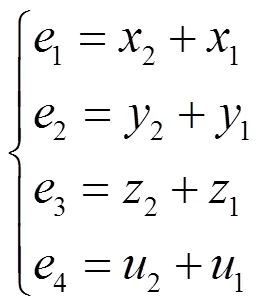
则可得到误差系统为

设计了如下一个非线性控制器

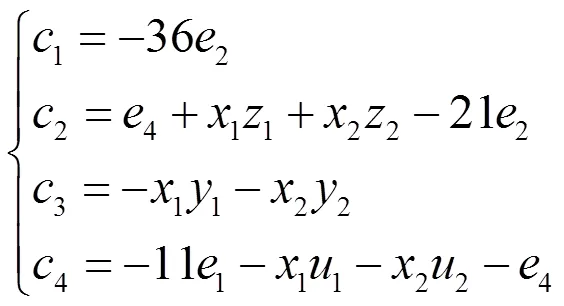
将式（4）代入系统（3），则误差系统可简化为

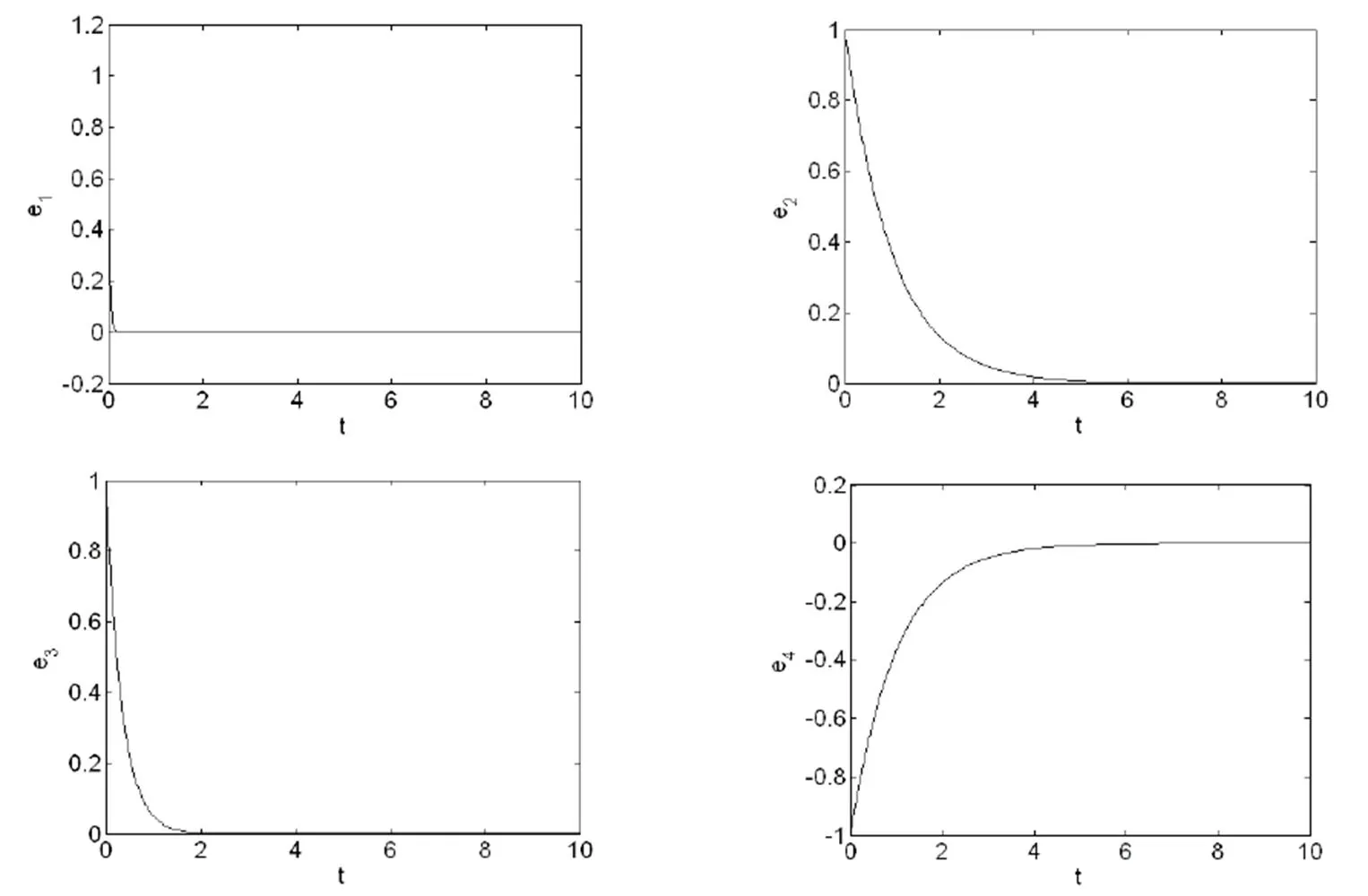
图2 系统(1)和(2)的自反同步误差曲线

2.2 系统异结构反同步

设系统(1)为驱动系统，取如下的系统[14](6)为响应系统

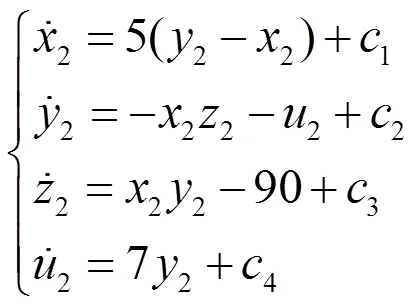
则误差系统为

设计了如下一个非线性控制器

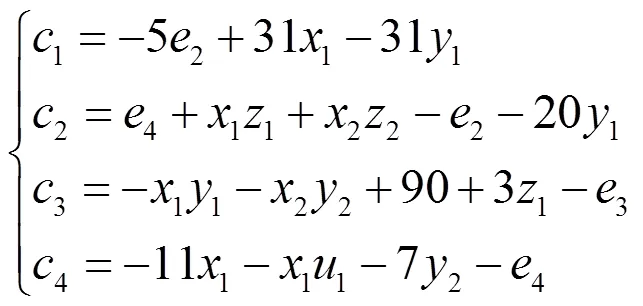
将式（8）代入系统（7），则误差系统可简化为

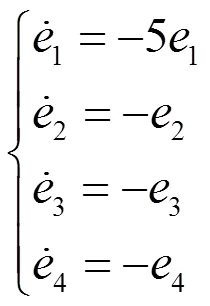
图3 系统(1)和(6)的异结构反同步误差曲线

Fig.3 Anti-synchronization error curveswith different structure of driving system (1) and response system (6)

3 结论

本文基于线性系统稳定性定理，设计了一种非线性反馈控制器，实现了超混沌Lü系统的自反同步和异结构反同步，该方法易于操作和推广，且速度快，结果稳定。该系统反同步的电路实验以及在混沌同步保密通讯方面的应用，作者下一步将作进一步的研究。

[1] 陈关荣,吕金虎.Lorenz系统族的动力学分析、控制与同步[M].北京:科学出版社,2003.

[2] Carrol T L,Pecora L M.Synchronization in chaotic systems[J].Physics Review Letters, 1990,64( 8):821- 824.

[3] 高智中.超混沌Liu系统的自同步研究[J]．湖南文理学院学报,2011,23(2):28-30.

[4] 高智中.一类新超混沌系统及其自同步[J]．常熟理工学院学报,2011,25(8):31-34.

[5] 邵仕泉,高心,刘兴文.两个耦合的分数阶Chen 系统的混沌投影同步控制[J].物理学报, 2007,56(12): 6815-6819.

[6] 陈秀琴,沈志萍,李文林.具有噪声扰动的统一混沌系统的同步控制[J]. 电光与控制, 2008,15(8):49-52.

[7] 李春彪,徐克生,胡文.Sprott系统的恒Lyapunov指数谱混沌锁定及其反同步[J].物理学报,2011,60(12):1-11.

[8] 高智中.Lü混沌系统的同步与反同步[J]．井冈山大学学报:自然科学版,2011,32(4):38-40.

[9] 梅蓉,吴庆宪,姜长生.异结构时滞不确定混沌系统的同步/反同步控制及其应用[J].电光与控制,2011,18(5): 37-41.

[10] Li G H, Zhou S P.Anti-Synchronization in Different Chaotic Systems[J].Chaos , Solitons & Fractal s,2007, 36(2) :516-520.

[11] 高智中.一种新的超混沌系统的计算机仿真分析[J].井冈山大学学报:自然科学版,2011,32(5):29-31,45.

[12] Lü J,Chen G A. New chaotic attractor cioned[J]. International Journal of Bifurcation and Chaos,2002, 12(3):659-661.

[13] 郑大中.线性系统理论[M].北京:清华大学出版社,1992.

[14] 高智中.一个新超混沌系统[J].吉首大学学报,2011, 32(5):65-68.

STUDY OF ANTI-SYNCHRONIZATION IN HYPERCHAOTIC Lü SYSTEM

GAO Zhi-zhong

(College of Science, Anhui Science and Technology University, Fengyang,Anhui 233100, China)

We design the nonlinear controller analytically and realize the anti-synchronization of hyperchaotic Lü system, anti-synchronization with different structure based on stability theorem of the linear system. Theoretical analysis and numerical simulation are given. Results demonstrate that the nonlinear controller can achieve anti-synchronization of two systems effectively.

hyperchaotic Lü system; nonlinear controller; stability theorem of the linear system; anti- synchronization

1674-8085(2012)03-0016-05

N941.7

A

10.3969/j.issn.1674-8085.2012.03.004

2012-03-13；

2012-04-08

安徽省高校省级优秀青年人才基金项目(2012SQRL146))

高智中(1979-)，男，山西神池人，讲师，硕士，主要从事非线性动力系统分岔和混沌理论及其应用研究(E-mail: zhouting7606@163.com).