基于乘客心理的最佳公交乘车路线选择方法研究
(武汉理工大学交通学院 武汉 430063)
随着经济的快速发展和城市化进程的不断推进,城市居民的出行量逐年迅猛增长,我国越来越多的城市正在成为“堵”城.对于如何解决城市交通拥堵问题,通过借鉴国外的城市交通的发展经验,城市治堵的关键是要使公交成为城市市民出行的主导方式.改善公交服务、增强公共交通吸引力仍是进一步缓解交通拥堵的“主攻”方向.
城市公交信息系统是指在乘客出行前或者出行中提供多种出行信息的综合交通服务系统,能够为乘客提供更加准确、及时、优化的公交信息服务.公交乘客的出行线路选择,是城市公交信息系统的关键技术之一.公交线路的逐渐增多,给人们的出行带来了极大便利的同时,因线路众多,给人们在选择出行乘车线路时带来了一定的困扰.因此,提供方便、快捷、经济、高效的公交出行线路方案,不仅能方便市民特别是外来旅游、出差、就医等的人的出行和生活,也为城市减少不必要的交通堵塞,有利于提高城市交通运输效率.同时,展示了现代城市信息化的风貌,提升城市形象[1].
1 公交乘客的心理特征研究
1.1 公交乘客的心理状况调查
确定公交出行最佳路线,很重要的一点是通过对乘公交车出行的乘客的心理行为进行调查研究,确定优化的目标和条件[2].
乘客出行心理,是乘客在出行过程中的心理活动规律和个性心理特征.公交乘客的出行,就其目的来看,主要包括上下班、购物、旅行等,无论从何种目的出发,乘客的心理特征主要都包括时效心理、实惠心理、舒适心理以及愉悦心理等[3-4].
对武汉市公交乘客的心理行为进行随机抽样调查,调查的内容包括乘客的年龄段、出行目的、选择出行路线的主要因素以及乘客对出行线路的各种主要影响因素的关注程度等.对调查数据进行统计分析后,结果显示,公交乘客的年龄段主要分布在15~45周岁,其出行目的主要有上下班、上下学以及购物、旅行等,影响乘客对出行路线选择的各种主要因素,按照乘客的关注程度从大到小排列依次为出行时间、出行距离、出行费用、换乘次数、乘车的便利程度、乘车的舒适度及地面交通的拥挤程度等.
1.2 最佳乘车路径指标的选取
基于上面的调查,选取公交乘客最为关注的出行时间、出行费用、出行距离3个最主要的指标,也就是最能影响公交乘客进行公交线路选择的主要指标,通过统计分析,得出上述3个指标对最佳公交乘车路线的权重,见表1.

表1 出行影响因素对乘车线路的选择权重比例
由表1可见,有半数以上的公交乘客对出行时间表示关注.随着城市生活节奏的加快,时间的价值越来越高,无论是上班、购物,人们对出行的效率越来越重视,选择最快捷的交通方式和出行线路,符合人们时效性的心理需求.
出行距离是指乘客从出行起点出发,到达出行终点的总距离,包括步行距离和乘车距离2部分.调查发现,人们通常更关注步行距离,其次是乘车距离,这符合乘客出行的舒适性和愉悦性的需求.
出行费用反映了出行的经济性.人们往往选择出行费用最小的出行线路,这符合乘客出行的实惠性的需求.
其次,在抽样调查中发现,人们对公交车的换乘次数也非常关注.换乘次数是乘客从出行起点出发,到达出行终点所需要换乘公交车的次数,这反映了出行的便利程度.通过调查分析,对于有多条公交出行线路的同一起讫点,乘客所能接受的最多换乘次数为3次.
综上所述,公交乘客的出行,往往选择出行时间最短、出行距离最短、出行费用最小、换乘次数最少的公交线路,该路径即为最佳公交乘车路径.
2 最佳公交乘车路线评价体系
2.1 评价体系的建立
从公交乘客的心理出发,建立最佳公交乘车线路评价体系,其目标主要是满足公交乘客的4个出行心理,即时效心理、实惠心理、舒适心理及愉悦心理.通过上面分析,作出如下假设:(1)同一公交线路上的各个公交站点的平均停靠时间基本相同;(2)道路状况相同公交线路公交车的运行速度基本相同.
根据层次分析法的思想,最佳公交乘车路线的评价体系分为3层,第一层为目标层(A),第二层为准则层(B),第三层为指标层(C).基于以上2点假设,建立最佳公交乘车路线的评价体系如图1所示.该评价体系的目标就是最佳公交乘车路线(A);准则层包括3个因素,即出行时间(B1)、出行费用(B2)和出行距离(B3);指标层共有6个指标,即站点数(C1)、道路阻抗(C2)、换乘次数(C3)、公交定价(C4)、乘车距离(C5)以及步行距离(C6).

图1 最佳公交乘车路线评价体系
其中,道路阻抗主要指公交线路的道路拥挤程度,公交定价指的是公交公司给不同的公交线路制定的不同价格.
2.2 构建判断矩阵
建立评价体系之后,按照1~9的比例标度对各个元素的重要性程度进行赋值,1~9比例标度的含义见表2.根据专家意见,构造两两比较的判断矩阵.

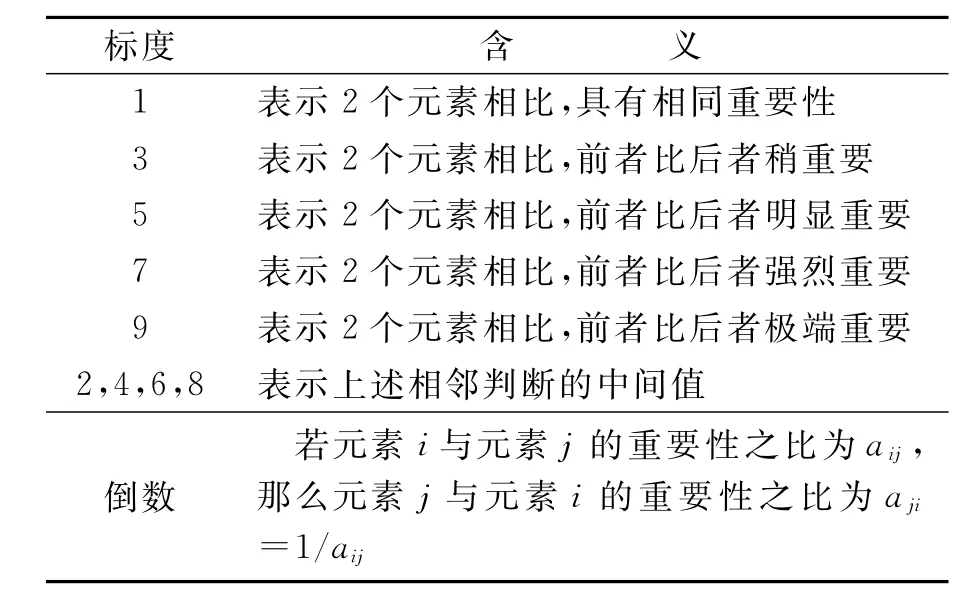
表2 1~9比例标度的含义
可以看出这4个矩阵都是一致性矩阵,根据最大特征向量法,可以计算出第二层对目标层的排序权重向量W2=(0.6,0.1,0.3),第三层对目标层的排序权重向量 W3=(0.12,0.24,0.26,0.02,0.18,0.18)[5].
3 模糊决策算法研究
3.1 隶属函数的确定
将公交乘客的出行线路选择看作是乘客的一次决策,其决策的目标就是最佳公交路线.在全面评价一个对象时,要着眼于所有的因素,但作出最后结论时,这些因素的参考价值是不同的[6].考虑到作出最佳公交乘车路线决策时,指标层的6各指标除道路阻抗之外,其他5个因素是可以直接量化的,因此选择这6个指标作为决策依据.
设评价时所考虑的6个因素的集合为F={f1,f2,f3,f4,f5,f6},5个评语集合为 K={非常满意,满意,基本满意,不满意,极端不满意}.采用100分制计分法对评语进行打分,则得到一个关于评语分数的向量K=(k1,k2,k3,k4,k5),即

在最佳公交乘车路线评价时,每个因素对各个评语的隶属度关系称为隶属函数,则建立6个指标的隶属度函数见表3.
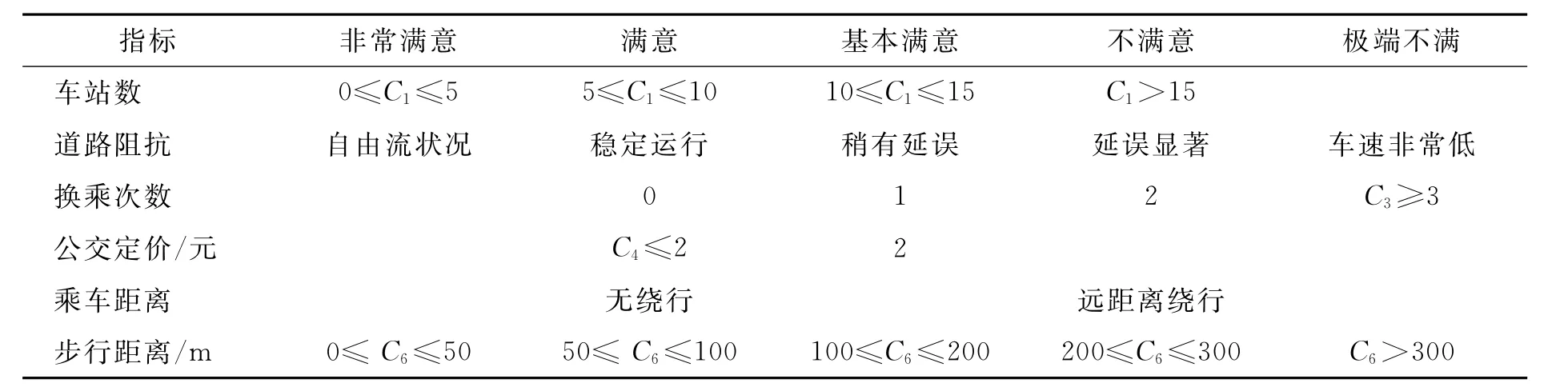
表3 各个因素的隶属度函数表
3.2 模糊决策的数学模型
若用rij表示第i个因素对第j个评语的隶属度,则得到评语集对因素集的评价矩阵

本文采用0-1法表示,即因素i所属于的评语j用1表示,其他的为0.将各个指标相对于目标层权重W3看作是因素集,于是建立模糊评价方程

由于这种评判结果比较粗,因此,对评判结果进行量化处理.根据3.1所得出的评语分数向量,建立量化方程
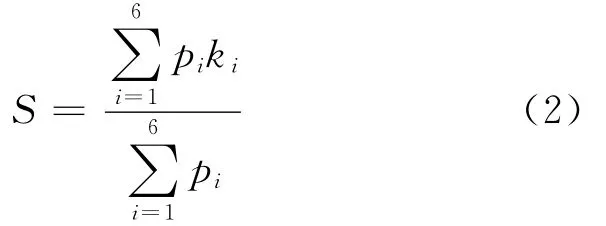
由于各个评语的得分是一个区间,这里取Ki为各个区间的上限[7].
4 应用举例
图2为A,B2地之间的一个简单的公交线路示意图,其各项指标的情况见表4,求A,B2地的最佳公交乘车路线.

图2 公交乘车路线示意图

表4 各公交线路的指标情况
以L1线路为例,根据各个因素隶属的情况建立模糊评价矩阵
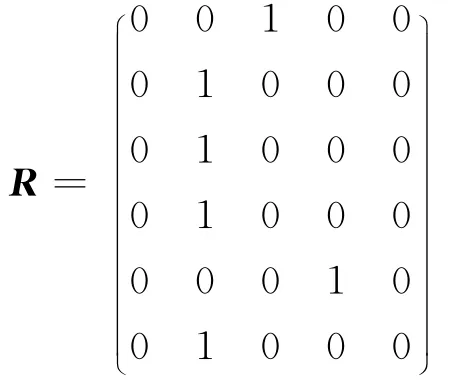
由式(1)和W3=(0.12,0.24,0.26,0.02,0.18,0.18),计算出隶属度向量P=(0,0.3,0.12,0.18,0),再由式(2)计算出量化分数S1=74.5.同理可以计算出L2线路的量化分数S2=72.4,L3线路的量化分数S3=74.8.
由上面计算可以看出,若由传统的Dijkstra算法可知,L2是最短乘车路线,但是综合考虑其他的各种因素,L3才是最佳乘车路线.
5 结束语
在求解最佳公交乘车路线时,传统的Dijkstra,Floyd算法往往只针对出行距离对路段进行赋值,寻求最短路径,而忽略了换乘次数、道路阻抗等重要因素,因而得到的结果可靠性较低.模糊决策算法能对多个影响因素进行综合考虑,并能兼顾考虑到各个因素的波动性和不确定性,因而求解出的最佳路线往往跟实际情况更相符,因而更具有可靠性[8].
然而,模糊决策算法也有其局限性,如在确定几条线路的各个指标的隶属度时,部分只能根据以往的调查或者经验得出,而不能实时的反映某一时段的真实路况,如道路阻抗等,所以在今后的研究中有必要考虑到道路状况的准确性和实时性.
[1]张白羽.基于Web GIS的杭州公交线路查询系统设计与实现[D].上海:复旦大学软件学院,2006.
[2]王 祥.公交车最佳乘车路径优化算法[J].唐山师范学院学报,2009,31(2):79-82.
[3]龚国清,张 伟.乘客出行心理研究的重要性及对策分析[J].公路与汽车,2004(1):85-86.
[4]Lin Jun,Xu Liangjie,Zhang Huanyu,et al.Simulation and evaluation for the design of passengers guidance departure from railway station based on 3DS MAX[C]//2009Second International Conference on Intelligent Computation Technology and Automation,2009:209-211.
[5]郭齐胜,董志明.系统建模与仿真[M].北京:国防工业出版社,2007.
[6]徐良杰,王 炜.基于一种新的混合算法的交通流控制优化模型[J].信息与控制,2005,36(3):286-291.
[7]吴其昌,陈天泽,粟 毅.基于多目标模糊决策的最佳路径分析[J].计算机仿真,2005,31(2):106-109.
[8]徐良杰,李兆康,王 炜.利用混沌搜索全局最优的交通流控制优化模型[J].武汉理工大学学报:交通科学与工程版,2008,32(3):413-416.

