基于Loop细分算法的曲面边界控制及曲面拼接

韩越兴， 刘秀平

（1.日本产业技术综合研究所 知 能系统研究部门，日本 东 京 305－8568；2.大连理工大学 数 学科学学院，辽宁 大 连 116024）

按照是否有边界，曲面可被分为有边界曲面（即非闭合曲面）和无边界曲面（即闭合曲面）。在用各种方法进行曲面造型的过程中，常常要求有边界曲面的边界能够形成满足人们要求的曲线，同时要保证原有曲面的光滑度和美感。

本文用细分曲面的方法构造这种类型的曲面，由于在计算机绘图中，往往用折线近似代替曲线，因此，把模型曲面边界要实现的形状叫做边界条件多边形。

细分曲面是一个网格序列的极限，网格序列则通过采用一组规则（一般是加权平均）在给定初始网格中插入新顶点，并不断重复此过程而获得。文献［1］提出了Catmull－Clark型细分模式以来，大量的细分模式及其改进涌现出来。同时，细分曲面造型方法的应用也得到了广泛推广。

文献［2］提出了满足边界条件是参数曲线的细分曲面造型方法，此方法可以使最终的曲面边界与边界条件曲线重合，但是在应用中要不断地和参数曲线联系起来，忽略了细分方法的“离散→离散”的特点，减弱了细分模式的优点，增加了曲面造型的难度。

文献［3－4］提出了基于Loop细分模式的满足边界条件的拼接算法，认为边界条件是封闭的多边形，在拼接过程中能够和细分方法巧妙地结合起来，算法容易实现，效率比较高。但是，文献［3］中的算法要求条件过于严格，即要求模型曲面的所有边界点在边界条件多边形上。在大多数情况下，曲面的边界点很少是在边界条件多边形上，这就需要通过合理地变化曲面，使边界点落在边界条件多边形上，并保持曲面的美感和光滑度。

本文提出了边界点不在边界条件多边形上的拼接算法，因为在实际应用的过程中，很容易能够保证模型曲面的一个边界点和边界条件多边形的一个顶点重合，因此，本文中要求至少有一个模型曲面边界点和边界条件多边形的顶点重合，同时要求模型曲面的边界顶点个数少于边界条件多边形的顶点个数。实际上，既然模型曲面是要被赋予细分计算，这个模型曲面往往是比较粗糙的，因此，最后这一要求是很容易成立的。

本文用到的Loop细分曲面是箱样条（Box spline）曲面的推广［4］，它在曲面造型中得到广泛应用，例如文献［5－6］。

在曲面造型中，往往需要把2个模型曲面拼接成一张曲面。如人们想在曲面本身不变的情况下再加上一个特征曲面，这就涉及曲面之间的拼接。有的时候，在处理空间网格生成一个曲面时，原有的模型曲面往往并不是一个封闭、完整的空间网格，甚至是一个有缺陷的网格，这就需要对模型曲面进行修补来产生一个封闭、完整的模型曲面，这时对网格的修补也要利用曲面的拼接。拼接后模型曲面的2个部分或者2个模型曲面既要求合为一体，还要求在拼接处满足一定的光滑性。本文提出新的算法，使2个模型曲面拼接后得到的曲面具有更好的光滑性。

1 满足边界条件的拼接算法

1.1 满足边界条件的拼接算法

算法1 利用下标法满足边界条件的拼接算法。

满足边界条件拼接最简单的方法，是按顺序把相应的2个点利用边界点数组下标和边界条件多边形的顶点数组下标找出来并直接相连，如图1所示。图1中粗线是边界条件多边形的一部分，细线是模型曲面的边界多边形的一部分，黑点分别是边界条件多边形的顶点和模型曲面的边界点。假设某个模型曲面的边界点与边界条件多边形的某个顶点重合，如图1a所示，其算法是把模型曲面边界点和相应的边界条件多边形上的顶点相重合。如图1b所示，利用模型曲面上的边界点个数和边界条件多边形相应部分的顶点个数平均分配来重合，计算如下：

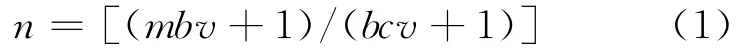
其中，mbv为在v1和v2之间其他模型曲面边界点的个数；bcv为c1和c2之间其他边界条件多边形顶点的个数；［］表示取四舍五入运算符。图1中v1、v2是模型曲面边界点和边界条件多边形顶点相重合的相邻的2个点；c1、c2是分别与v1和v2相对的边界条件多边形的顶点。图1中，在v1和v2之间模型曲面边界上顺序地每数一个边界点，则在c1和c2之间同方向顺序数边界条件多边形的n个顶点，然后把曲面边界点移到相应的边界条件多边形的顶点上。

在这 里，v1、v2、c1、c2只是表示点 的 标 记，后面另有其他含义。

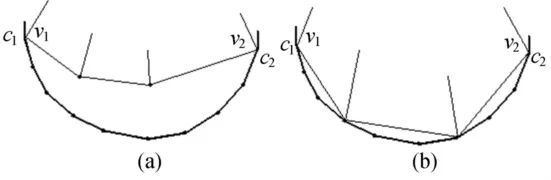
图1 算法1示意图

下面分2种情形进行细分。

情形Ⅰ 如果至少1个模型曲面的边界点不在边界条件多边形上，则整个模型曲面不进行经典的Loop细分。细分步骤如下：

（1）把任意一个与边界条件多边形上的顶点重合的模型曲面边界点作为第1个模型曲面的边界点，并以此点为起点，把所有的曲面边界点顺序排列（图1中按逆时针排列），存放入 Array－Boundary［］数组中。

（2）把与 ArrayBoundary［0］位置相同的边界条件多边形的顶点作为第1个边界条件多边形的顶点，并以此点为起点，把所有的边界条件多边形的顶点按顺序排列（图1中按逆时针排列），存放入BoundaryConditions［］数组中。

（3）从ArrayBoundary［0］出发，遍历 Array－Boundary［］中的点，依次找到所有与边界条件多边形上的顶点重合的模型曲面边界点，如果每2个相邻的与边界条件多边形上的顶点重合的模型曲面边界点之间没有ArrayBoundary［］其他的点，则不予考虑；如果有，则进行下去。

（4）假设相邻的与边界条件多边形的顶点重合的曲面边界点为ArrayBoundary［v1］和Array－Boundary［v2］，如果 ArrayBoundary［v1］是 Array－Boundary［］中最后一个点，则v2＝0；否则v2＞v1。

（5）找到与 ArrayBoundary［v1］和 Array－Boundary［v2］分别重合的 BoundaryConditions［c1］和BoundaryConditions［c2］，如果 Boundary－Conditions［c1］是 BoundaryConditions［］中最后一个点，则c2＝0；否则c2＞c1。

（6）利用（1）式，把 ArrayBoundary［］点直接移到相应的BoundaryConditions［］点的位置上。

情形Ⅱ 如果所有的模型曲面上的边界点都在边界条件多边形的顶点上，则直接应用文献［3］中的算法进行Loop曲面拼接。

对于算法1，当模型曲面边界点和边界条件多边形的顶点分布比较均匀时，效果比较好，但是不满足这个条件时，图形可能会变形，如图2所示。

图2 模型曲面变形示意图

由图2a可见，当边界条件多边形（图中用粗线表示）的顶点集中在右面，而模型曲面边界点集中在左面。利用算法1曲面造型后，细分曲面在靠近边界处将发生扭转。

另外，利用（1）式时，当mbv＋1能够整除bcv＋1时效果是很好的，但是当不能够整除时，与最后一个模型曲面边界点进行重合的边界条件多边形的顶点，到终点之间的顶点可能过多或者是过少。

特别当边界条件多边形的顶点很多时，这种情况愈发突出，这种情况可以由图2c～图2f可见。因此，提出了下面的算法。

1.2 对算法1的改进

算法2 利用模型曲面边界边的累加边长与边界条件多边形的累加边长之间的关系，实现满足边界条件的细分曲面拼接。

如图3所示，计算v1和v2之间的模型曲面边界边的总长度，把c1和c2之间边界条件多边形的总长度也算出来，然后从v1出发，顺序找到曲面的边界点，把它的累加边长（图中A点时，就是v1到A的长度，当是B点时，就是v1到A的长度加上A到B的长度，以此类推）比上v1到v2总模型曲面边界边长，记为mc。

再找到累加边长与c1到c2的边界条件多边形总长度的比分别大于mc和小于mc，并与mc最接近的边界条件多边形的2个顶点。在这2个边界条件多边形的顶点中找到与它们相对应的模型曲面边界点最近的那个点，此点的位置就是相对应的模型曲面的边界点要移动的位置。例如图3中的A点，通过累加边长的方法可以找到2个边界条件多边形的顶点，即A′点和A′与c1之间的那个点，然后通过比较A点到2个点的距离找到最近的那个点，即A′点。同样也可以找到B点的对应点B′点，移动A点到A′点、B点到B′点即可。

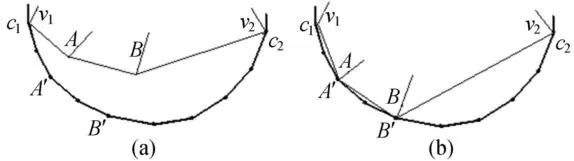
图3 算法2示意图

下面分2种情形进行细分。

情况Ⅰ 如果至少1个模型曲面的边界点不在边界条件多边形上，则整个曲面不进行经典的Loop细分。细分步骤如下：

（1）把任意一个与边界条件多边形上的顶点重合的模型曲面边界点定义作为第1个曲面的边界点，以此点为起点，把所有的模型曲面边界点顺序排列（在图3中按逆时针排列），存放入Array－Boundary［］数组中。

（2）把与 ArrayBoundary［0］位置相同的边界条件多边形的顶点作为第1个边界条件多边形的顶点，并以此点为起点，把所有边界条件多边形的顶点按顺序排列（在图3中按逆时针排列），存放入BoundaryConditions［］数组中。

（3）从ArrayBoundary［0］出发，遍历 Array－Boundary［］中的点，依次找到所有与边界条件多边形上的顶点重合的模型曲面边界点，如果每个相邻的与边界条件多边形上的顶点重合的模型曲面边界点之间没有ArrayBoundary［］其他的点，则不予考虑；如果有，则进行下去。

（4）假设相邻的与边界条件多边形的顶点重合的模型曲面边界点为ArrayBoundary［v1］和ArrayBoundary［v2］，如果 ArrayBoundary［v1］是ArrayBoundary［］中最后一个点，则v2＝0；否则v2＞v1。

（5）找到与 ArrayBoundary［v1］和 Array－Boundary［v2］分别重合的 BoundaryConditions［c1］和BoundaryConditions［c2］，如果 Boundary－Conditions［c1］是 BoundaryConditions［］中最后一个点，则c2＝0；否则c2＞c1。

（6）把 从 ArrayBoundary［v1］到 Array－Boundary［v2］之间的边界边总长度存入La。

（7）把从BoundaryConditions［c1］到BoundaryConditions［c2］之间的边界条件多边形的总边长存入Lb。

（8）从 ArrayBoundary［v1＋1］出发，到 ArrayBoundary［v2］上一点为止，计算每一模型曲面边界点的累加边长与La的比值，并存放入一临时数组TArray－m［］中。

（9）从BoundaryConditions［c1＋1］出发，到BoundaryConditions［c2］上一点为止，计算每一个边界条件多边形顶点的累加边长与Lb的比值，并存放入另一临时数组TArray－b［］中。

（10）从TArray－m［0］开始，遍历整个 TArray－m［］数组，对每个 TArray－m［i］（i是下标），遍历TArray－b［］数组，找到比TArray－m［i］小的最大的元素 TArray－b［ii］（ii是下标）和下一个元素 TArray－b［ii＋1］，如果ii＋1是 TArray－b［］的元素数量，则TArray－b［ii＋1］为1。

（11）对于BoundaryConditions［c1＋ii＋1］和BoundaryConditions［c1＋ii＋2］，如果其中一个点已经和某个模型曲面边界点重合，则把ArrayBoundary［v1＋i＋1］点移动到另一个点上，否则，把 ArrayBoundary［v1＋i＋1］点移动到离它最近的点。

情形Ⅱ 如果所有的模型曲面上的边界点都在边界条件多边形的顶点上，则直接应用文献［3］中的算法进行Loop曲面的拼接。

在情形Ⅰ的步骤（11）中，如果模型曲面边界点和边界条件多边形顶点之间的位置不是很理想，可能出现BoundaryConditions［c1＋ii＋1］和BoundaryConditions［c1＋ii＋2］点都已经和某2个模型曲面边界点重合。如图4所示，C和D本来要对应的点是A′和B′，但是这2个点都已经与A和B重合了。

如果把2个模型曲面边界点都和1个边界多边形的顶点重合，不可避免地出现褶皱，这时将用算法3来修正。

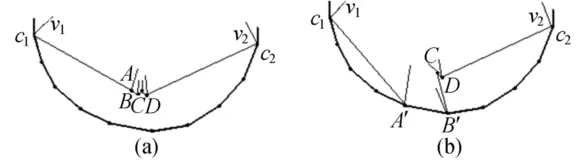
图4 算法2的不足示意图

1.3 满足边界条件指定对应点的拼接算法

算法3 让模型曲面上的边界点对应边界条件多边形上特指的顶点，并能对模型曲面边界加以控制。下面分3种情形进行细分。

情形Ⅰ 如果至少1个模型曲面的边界点不在边界条件多边形上，并且至少1个边界点上有标志，则整个模型曲面不进行经典的Loop细分。细分步骤如下：

（1）把模型曲面的边界点存放入 Array－Boundary［］数组中。

（2）把边界条件多边形的顶点存放入BoundaryConditions［］数组中。

（3）从ArrayBoundary［0］出发，遍历 Array－Boundary［］中的点，如果遇到有标志的点，则从BoundaryConditions［0］出发，遍历BoundaryConditions［］中的点，找到有相同标志的点，移动ArrayBoundary［］中的这个点，使2点重合，除去2点上的标志。

情形Ⅱ 同算法1或者算法2中的情形Ⅱ。

情形Ⅲ 经过情形Ⅰ、Ⅱ后，如果至少1个模型曲面的边界点不在边界条件多边形上，同算法1或者算法2，根据具体情况而定。

对于算法3，在实际编程中，可以作进一步改进，把BoundaryConditions［］中全部带有标志的点取出来，放入另一个临时数组T［］里，在程序运行到情形Ⅰ中的步骤（3）时，只要把遍历BoundaryConditions［］的点改为遍历T［］数组，这样就减少了程序运算时间，提高了程序效率。

因为文献［3］中的算法及算法1和算法2都要进行边界点排序，最好在开始就进行点的排序，这样可以增加算法3的程序通用性和效率。

1.4 算法实现

如图5所示，利用算法1、算法2很容易构造出满足边界条件的细分曲面，并且光滑程度很好，可以看出在边界点分布比较均匀的情况下，用算法1和算法2实现的曲面很接近。

图5a左上角的图形是原始模型曲面，首先用算法1实现曲面造型，然后用算法2实现同一个模型曲面的曲面造型，如图5b所示。在图5c中，左上角的图形是原始模型曲面，粗线是边界条件多边形，圆点是含有标志的点；第2个图形是经过算法3后模型曲面所有的边界点都在边界条件多边形上；经过进一步细分后，生成了一个满足边界条件的光滑曲面。

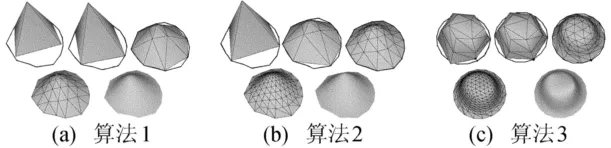
图5 3种算法实现示意图

2 2个曲面的拼接算法

基于上述算法，能够实现2个模型曲面的边界点不全在同一个多边形上的曲面拼接算法。

2.1 算法介绍

对于模型曲面，有以下定义：

（1）f－model。对于边界点数量少的模型曲面，此曲面上的点数、边数、面数都比较少。

（2）m－model。对于边界点数量多的模型曲面，此曲面上的点数、边数、面数都比较多。

本文要求至少有1对2个模型曲面边界点是重合的，如果2个模型曲面的边界点只有1对重合，那么，f－model边界点的个数要少于 m－model边界点的个数。

如果有多对重合点，则要求相邻的2对fmodel与m－model重合的边界点之间，f－model的边界点的个数要少于相应段上的m－model边界点的个数。

当f－model上至少有1个边界点不在 mmodel的边界边上时，需要把m－model的边界边看作f－model的边界条件多边形，根据不同的条件和要求，利用前文中不同的算法实现2个模型曲面的边界点都在同一个多边形上，最后再利用文献［3］的算法即可。

2.1.1 算法4

（1）把 m－model的边界看作f－model的边界要重合的边界条件多边形，对f－model应用算法1、算法2中的情形Ⅰ，经过此步，m－model和fmodel的边界点在同一个多边形上。

（2）把 m－model的边界看作f－model的边界要重合的边界条件多边形，对f－model应用文献［3］的算法。

（3）把f－model上与边界点相连的新生成的非边界点，利用文献［3］中的（1）式进行调整。

（4）如果f－model与 m－model的边界没有重合，回到步骤（2）；否则，进行下一步。

（5）把2个曲面合成一个模型曲面。

（6）把整个模型曲面进行Loop细分，直到满意为止。

2.1.2 算法5

通过上述算法，拼接后得到的曲面在非特殊点处，可以达到C2，而在特殊点处是C1光滑。

如果要完成重合2个模型曲面的指定边界点，可以利用算法5。

（1）把 m－model的边界看作f－model的边界要重合的边界条件多边形，对f－model应用算法3中的情形Ⅰ，经过此步，m－model和f－model上带有标志的边界点在同1个点上。

（2）利用算法1完成2个曲面的拼接。

在上述2个算法实现过程中，经常会出现几个f－model边界点对应1个m－model边界点，应该尽量避免，否则会出现大的褶皱。

2.2 算法实现

算法实现图例如图6所示。

图6 算法实现图例

图6a左上角图形是原始的2个模型曲面俯瞰图；右上角图形是原始的2个模型曲面的侧视图；左下角的图形是经过算法后f－model的边界点都在m－model的边界点上；右下角的图形是2个曲面经过拼接细分后产生的曲面模型。图6b是利用拼接算法的图例。

3 结束语

本文提出了多个算法来控制曲面边界形状，同时又能保持模型曲面的发展趋势，在此基础上又提出了细分曲面之间的拼接。根据Loop细分曲面特性，拼接后得到的曲面在非特殊点处可以达到C2，而在特殊点处是C1光滑。通过这些算法，不仅能够控制曲面边界的形状，增加曲面的特征，还能填补曲面的漏洞。

尽管本文所提出的算法是基于Loop细分模式，但它们很容易在其他细分模式中得到推广。

［1］ Catmull E，Clark J.Recursively gengerated B－spline surfaces on arbitrary topological meshes［J］.Computer Aided Design，1978，10（6）：350－355.

［2］ Levin A.Combined subdivision schemes for the design of surfaces satisfying boundary conditions［J］.Computer Aided Geometric Design，1999，16：345－354.

［3］ 韩越兴，刘秀平，施锡泉.Loop细分模型的边界拼接算法［J］.大连理工大学学报，2004，44（1）：12－16.

［4］ Loop C.Smooth spline surfaces based on triangles［D］.Department of Mathematics，University of Utah，1987.

［5］ 赵向军.Loop型半静态细分方法［J］.计算机辅助设计与图形学学报，2006，18（7）：929－935.

［6］ 赵付青，艾 鑫.可调自适应三角网格的细分曲面造型方法［J］.计算机工程与设计，2011，32（1）：232－235.