空基助推段拦截中制导律设计
李宪强,刘莹莹,葛致磊,周军
(西北工业大学精确制导与控制研究所,陕西西安 710072)
引言
弹道导弹从起飞到发动机关机这一飞行段称为助推段。空基助推段拦截具有拦截范围广、拦截几率大等特点[1]。但是在空基助推段拦截制导律设计过程中会遇到以下几个难题:(1)可用信息较少。由于载机离敌方阵地较近,因此会受到强烈的电子干扰,此时能获得的目标运动信息较少,有时甚至只能得到目标的位置信息;(2)弹目速度比较小。空射型拦截弹所携带的燃料受自身质量的限制,从而使末端弹目速度比较小;(3)制导律需要具有较大的预测能力和抗干扰能力。由于处于助推段的目标沿弹体轴向的加速度很大,相应地其沿着视线法向和纵向的分量都很大,因此需要中制导律具有较大的预测能力和抗干扰能力,以抵抗目标很大的加速度对视线转率的扰动。
针对以上情况,如果采用基于预测命中时间的比例中制导律,则会因目标运动信息较少,导致预测命中时间存在很大误差,从而使末端脱靶量较大;而奇异摄动中制导律不但需要的目标运动信息较多,而且计算复杂,对弹上设备要求较高;弹道形成中制导律没有考虑阻力随大气密度的变化,其结果要次于奇异摄动中制导律[2-3]。鉴于此,本文提出了基于自抗扰控制器的中制导律设计方法。自抗扰控制器的核心思想是把系统中各种不同的干扰因素统一归类为对系统的“扰动”,然后用“扩张状态观测器”进行估计、补偿。在此基础上,进行动态反馈线性化,再使用非线性配置构成非线性状态误差反馈控制律来提高其闭环系统的控制性能。因此,针对空基助推段拦截过程中可用信息较少、干扰较大等问题,可以采用自抗扰控制器设计相应的制导律。仿真结果表明,本文所设计的中制导律具有制导精度高、需用目标信息较少和便于在线计算等优点。
1 数学模型
首先,忽略地球自转,建立地面坐标系,即原点O取发射时导弹的质心在地面(水平面)上的投影点,Ox轴在水平面内,指向拦截弹发射时目标在地面上的投影点;Oy轴与地面垂直,向上为正。
忽略导弹的滚转,则在纵向平面内拦截弹的运动方程为:
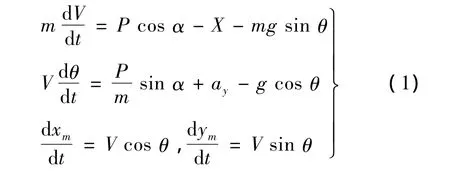
式中,m为导弹质量;V为导弹速度;P为发动机推力;α为迎角;X为阻力;g为重力加速度;θ为弹道倾角;ay为指令加速度。
设任意时刻在地面坐标系内,导弹和目标的位置分别为(xm,ym)和(xt,yt),如图1所示。则弹目相对距离为:
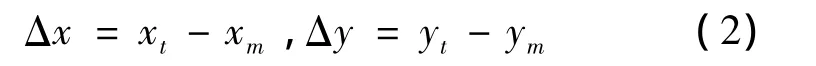
由图1可知,在纵向平面内,假如Δy相对于Δx能够快速地趋近并保持在零,则此时导弹和目标相当于沿着与Ox轴平行的基准线做相向运动,也就是采用平行接近的拦截方式进行拦截。

图1 纵向平面内弹目相对运动图
接下来对以上拦截方式的可行性进行定性分析,即讨论Δy相对于Δx能否快速趋近并保持为零。由于进行的是空基拦截,因此载机的高度一般在10 km左右,而目标被发现的高度一般也会在10 km左右,因此导弹和目标的初始高度差不会太大,一般在几公里以内,而弹目初始距离一般在几十公里甚至上百公里以外,因此只要设计出合适的制导律,就能够使 Δy相对于 Δx快速地趋近并保持为零。
基于以上分析可知,在纵向平面内,可以将导弹的制导律设计问题转换成如何求得使Δy快速趋近并保持为零时指令升力ny的问题。为了便于采用自抗扰控制器设计制导律,结合式(1)和式(2),建立更为直观的输入-输出方程。
令x1=Δy,x2=,输入为u=ay,输出为y=x1,则输入输出方程有如下形式:
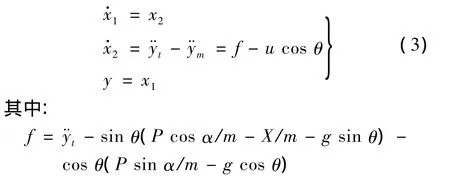
由于目标的加速度和速度不可得,因此将上式视为干扰项。
2 基于自抗扰控制的中制导律设计
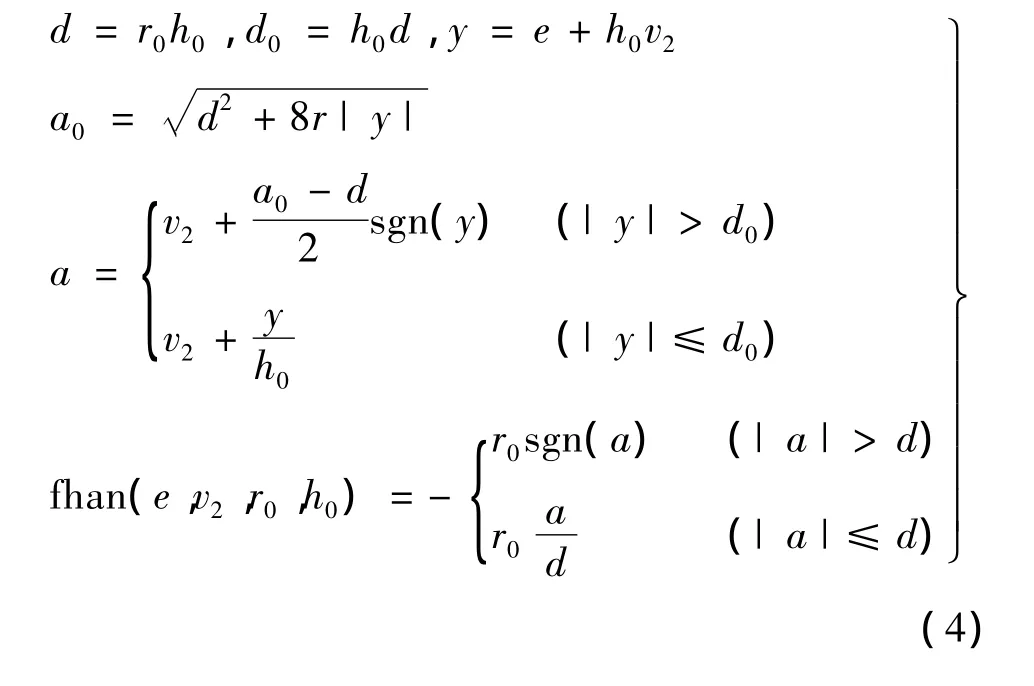
根据文献[4]中给出的自抗扰控制器的设计步骤,先给出最速控制综合函数表达式:式中,r0为速度因子,增大其值可以提高跟踪速度;h0为滤波因子,其值与仿真步长相对独立时,可提高输出曲线的平滑度。
利用最速控制综合函数,将Δy趋近于零的过渡过程规划成快而无超调的过程,规划过渡过程的方程如下:
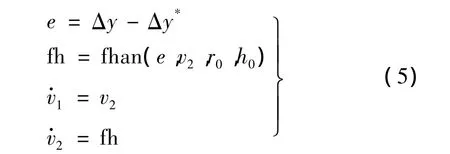
式中,Δy*=0;v1跟踪e;v2跟踪。
采用扩展状态观测器对式中的干扰项f以及由于受到电子干扰而不可测的状态x2进行观测,扩展状态观测器方程如下:
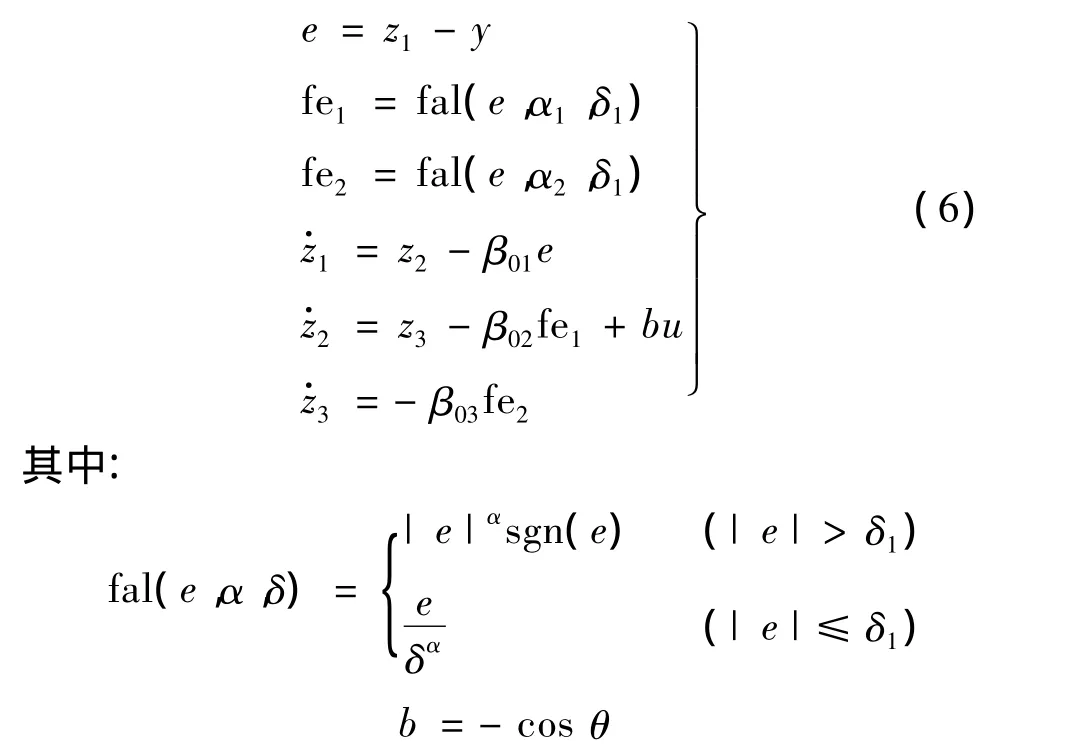
式中,β01,β02,β03为状态观测器参数;z1跟踪 x1;z2跟踪 x2;z3跟踪f。
自抗扰控制既可以采用非线性反馈控制律,也可以采用线性反馈控制律。采用非线性反馈控制律时,如果采用最速控制函数,由于最速控制综合函数的离散性太强,其容易引起控制信号的跳变,会给控制信号的实现带来困难,同时会给执行机构带来一定的危害,为了降低信号的跳变现象,现设计如下形式的状态误差反馈控制律:
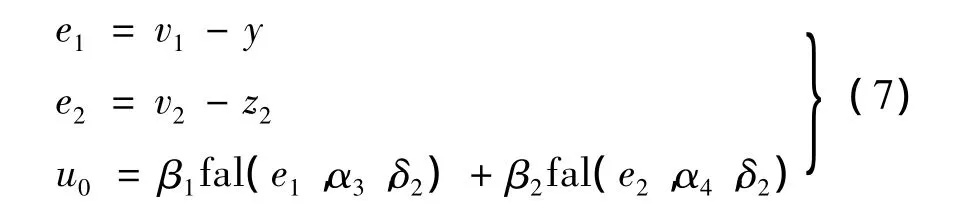
在调节 α3,α4,δ时,当 α3和 α4在[0,1]内取值较小时,控制律更趋向于bang-bang控制,因此控制器的效率会较大,但是会引起较大的振荡,此时可适当增大δ1和δ2来降低振荡幅值。
扰动补偿过程如下:

综上可知,基于自抗扰控制器设计制导律的Simulink仿真结构图如图2所示。

图2 空基拦截制导律仿真结构框图
3 仿真验证与结果分析
假设当目标为射程1 600 km的弹道导弹,其在飞行高度为9 km时被发现,拦截器初始速度为Ma=1,初始弹道倾角为2°,发动机推力为8 820 N,推力时间为25 s,初始高度为10 km,弹目初始距离为135 km。基于零控脱靶量的制导律仿真参数为:r0=80,h0=0.001,α1= α2=0.5,δ1=0.000 01,β01=100,β02=1 800,β03=1 600,δ2=0.000 01,α3= α4=0.8,β1=80,β2=20。设定过载限制为 12。仿真结果如图3~图5所示。
由图3可知,本文所设计的制导律能够很好地控制住弹目相对高度差,证明了自抗扰控制器的控制能力。由图4可知,当弹目相对高度差被控制住以后,弹目视线角速度也能够被稳定地控制住,证明了将弹目视线角速度的控制问题转换成高度差控制问题的可行性。由图5可知,拦截弹弹道曲线后半段非常平直,这样有利于降低脱靶量。拦截弹弹道曲线前半段比较弯曲,这是由于在拦截开始时,初始偏差较大,而且拦截弹处于加速状态,其沿竖直向上的加速度分量比目标沿竖直向上的加速度分量要大,因此需要不断地降低其本身的弹道倾角,才能保证相对高度差为零,继而才能保证视线角速率为零。这是由于拦截弹的加速时间相对拦截时间来说较短,而且还只是弹目沿竖直方向的相对加速度差才会对弹道的弯曲度造成影响,因此弹道曲线的弯曲段较短而且曲率不会太大,所以并不会对末端脱靶量造成过多影响。
此外,为了探讨采用文中的中制导律后能否有效降低末段脱靶量,基于以上仿真参数,在仿真过程中加入比例末制导律,其中,末制导的导航比为3.5,弹目距离为10 km时中末制导交接班,末段导引头盲区为300 m,过载限制为12,则仿真结果显示末段平均脱靶量为0.012 m。这一结果也说明了弹道曲线的弯曲段并未对末端脱靶量造成过多的影响。
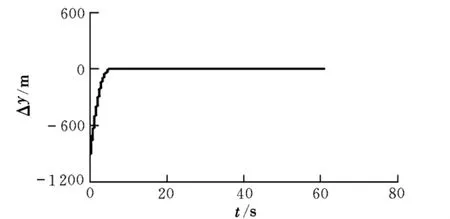
图3 弹目相对高度差曲线

图4 弹目视线角速度曲线
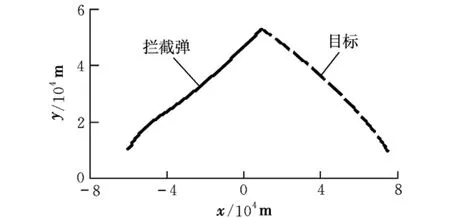
图5 拦截弹道曲线
4 结论
本文提出了一种采用自抗扰控制器设计空基助推段拦截中制导律的方法,并进行了仿真。从仿真结果来看:(1)在进行空基助推段拦截中制导律设计时,可以将竖直平面内的弹目视线角速度的控制问题转化成相对高度差的控制问题;(2)自抗扰控制器能够很好地解决在制导律设计过程中遇到的可获得的目标运动信息较少以及目标加速度较大等问题,并且显示了很高的导引精度,降低了末端脱靶量。仿真结果表明了文中基于自抗扰控制器所设计的中制导律能够很好地完成助推段拦截任务。
[1] Dean Wilkening.Airborne boost-phase ballisticmissile defense[J].Science and Global Security,2004,25(2):1-67.
[2] 李峰,王新龙.空空导弹中制导律的适用性研究[J].航空兵器,2009,15(6):3-7.
[3] John Lukacs,Oleg Yakimenko.Trajectory-shape-varying missile guidance for interception of ballistic missiles during the boost phase[C]//AIAA Guidance,Navigation and Control Conference and Exhibit.South Carolina:American Institute of Aeronautics and Astronautics,2007:1-21.
[4] 韩京清.自抗扰控制技术[M].北京:国防工业出版社,2008.

