自动微分技术及其在轨迹优化中的应用
王晨曦,李新国
(西北工业大学航天学院,陕西西安 710072)
引言
飞行器轨迹优化问题多采用依赖于导数信息数值优化算法来求解,特别是对于得到广泛应用的直接法,其基本思想是将求解无限维的函数优化问题转化为有限维参数非线性规划问题。在采用非线性规划算法求解时,需要计算目标函数及约束对参数的微分信息,微分信息计算的精度对非线性规划的精度及收敛性有较大影响。因此如何快速、准确、高效地计算微分信息,对于轨迹优化设计具有重要意义。
现有的导数计算方法种类繁多,但计算的效率、精度却存在差别,常见的方法有:有限差分法、符号微分法、复变量法和自动微分方法[1],其中自动微分法具有很高的计算精度,理论上可以达到机器精度,同时又方便编程实现,近年来在多学科设计优化[1]、飞行器气动外形优化[2]等数值优化领域得到广泛应用。本文将自动微分技术与内点非线性规划方法相结合,用于求解直接轨迹优化问题。
1 自动微分技术
自动微分(Automatic Differentiation,AD)又称算法微分,其理论和实现方法在近几年得到迅速发展。当前,各领域的工程设计问题越来越依赖于计算机,通常都是将问题的数学模型转化为计算机程序,然后基于计算程序来实现基于仿真的设计及优化。以计算机语言描述的数学模型不同于简单的数学表达式,而是成千上万行的程序代码,不可能依赖于手工求导,必须寻求适用于程序微分信息计算的新途径,自动微分技术恰好是这样一种技术。
自动微分的实质是基于链式法则(Chain Rule)自动生成计算程序微分信息或微分计算程序的技术。其基本思想是无论描述函数的计算机程序多复杂,它本质上都是执行一系列的初等计算、初等函数及逻辑运算的组合。对这些初等运算迭代运用链式求导法则,可以自动并精确地得到目标函数的任意阶微分信息,与其他微分计算方法相比具有明显优势[3]。
1.1 自动微分模式
当通过链式法则获取了复杂函数(程序)的微分计算关系之后,需要将初等函数微分进行连续累积得到复杂函数的微分信息,根据累积方向的不同可以分为前向模式(Forward Mode)和逆向模式(Reverse Mode)两种。
顾名思义,前向模式是按照从自变量(Independent Variable)到因变量(Dependent Variable)的方向应用链式法则逐次计算每个计算单元(初等函数)的局部偏导数,得到所需导数信息;逆向模式与前向模式相对应,是按照从因变量到自变量反方向逐次计算微分信息。首先前向执行函数代码列表,并记录中间变量^ti,然后通过^ti传递因变量与自变量之间的导数关系,反向累积获得微分信息(见表1)。

表1 自动微分的两种模式
两种计算模式各有特点,逆向模式计算量与设计变量的数目无关,适用于设计变量数目较多的情况;而前向模式适用于函数数目多于设计变量数目的情况。可根据对应问题的特点选择合适的计算模式。以下面的算例说明这两种计算模式[4]。
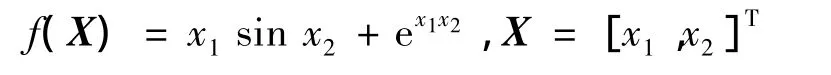
1.2 自动微分方法和工具
自动微分程序的实现方法分为两种:源代码转换法(Source Transformation Method,STM)和算子重载法(Operator Overloading Method,OOM)。
STM通过对程序代码进行分析,利用编译技术,将原计算程序转换为可进行函数导数计算的新函数(见图1),它可用于任何程序语言[5]。STM需要针对源代码程序语言的特性,设计专门的语法、词法分析器,由于具有针对性,因而可获得优化的计算程序,具有高的计算效率,但是对于某些语法灵活的程序语言(如CC++),设计自动微分代码转换的AD工具是一项非常有挑战性的工作。目前,针对C语言,通过代码转换策略实现的AD工具仅有美国Argonne国家实验室开发的ADIC。基于代码转化实现的软件包有:ADIC,ADIFOR,OpenAD和TAPENADE等。

图1 自动微分的代码转化实现方式
OOM是利用计算机程序语言的特性,采用算子重载技术实现微分的同步计算[5]。目前许多高级计算机程序语言均支持这一技术,如C++,Fortran-90,Ada和Matlab等。采用算子重载法无需改变原有程序的程序代码,而是通过声明特定类型的变量实现自动微分,如图2所示。例如本文采用的ADOL-C工具包[6],只需将期望获得微分信息的自变量和因变量声明为“active”变量,即可在程序运行时生成包含微分信息的“tape”文件,与STM技术实现的自动微分相比更加便于使用,不生成微分计算程序,但是这种方法无法通过编译实现微分计算过程的优化。基于算子重载实现的软件包有:ADC,ADF,ADOLC,FADBADU++,CppAD和MAD等。本文采用ADOL-C作为自动微分工具。

图2 自动微分的算子重载实现方式
2 轨迹优化方法
轨迹优化本质上是一种无限维的函数最优化问题,直接轨迹优化方法的基本思想是将函数优化问题转化为有限维参数优化问题。本文首先利用直接配点法将其转化为非线性规划问题,然后结合自动微分和内点非线性规划算法进行求解。
2.1 最优控制问题
最优控制问题的求解是找到满足一定约束的最优控制变量u*(t)及其对应的最优状态(轨迹)x*(t),并使目标函数最小。其中x(t)∈Rnx和u(t)∈Rnu为状态函数和控制函数向量,目标函数为:

2.2 直接配点法
直接配点法同时将状态变量和控制变量离散化后实现最优控制问题向参数优化问题的转化,将离散点处的状态及控制量同时作为优化设计参数。直接配点法的核心内容是通过一定的转化方式,将动力学约束转化为非线性规划的等式约束。根据不同的积分近似准则,直接配点法分为Trapezoidal法、Hermite-Simpson法[7]等局部配点法和 Legendre伪谱法[8]、Chebyshev 伪谱法[9]、Guass 伪谱法[10]等全局配点法。
通过直接配点法可将最优控制问题转化为下面的非线性规划问题(有关直接配点法的详细描述参见文献[7-10]):

本文采用C++编制了Trapezoidal法、Hermite-Simpson法、Legendre伪谱法的计算程序。
2.3 内点非线性规划
内点法[11]的基本思想是将有约束问题转换为一系列障碍问题 (Barrier Problem),在可行域内迭代求解障碍问题极值点的方法。
早期的内点法均采用精确罚函数法保证算法的收敛性,即将约束函数作为惩罚项,新的评价函数为目标函数与惩罚函数两项之和。近期由Fletcher等提出了过滤方法代替评价函数来保证求解NLP问题的收敛性,其核心思想是减小性能指标函数值或减小约束函数违背值的搜索点均将被算法接受,而非仅接受减小评价函数值的点。这使得内点法逐渐成为高效、稳定的求解大规模NLP问题的一种方法。内点法数学描述如下:
对于式(9)中描述的不等式约束 g(X)和h(X),为描述方便,令

式中,X为nx维实数向量;c为nc维实数向量。引入nx维松弛向量s将不等式约束转换为等式约束,即c(X)=¯(X)-s=0,s≤0,则优化问题可表示为仅包含等式约束的优化问题:

内点法将上述问题转换为求解一系列障碍问题的极值:

在内点法的求解过程中,障碍参数μ>0逐渐减小并趋于零,障碍项用于防止设计变量X(i)达到边界,从而保证其始终在可行域内。应用Homology方法可得到问题(12)的主-对偶极值点条件:

式中,λ∈Rnc和z∈Rnx分别为式(11)中等式约束及边界约束对应的拉格朗日乘子向量;:=diag(X)(表示取 X对角线元素构成对角矩阵),同理:=diag(z);e为单位向量。当式(13)中的Homology参数μ=0时,式(13)和X,z≥0就可以构成原问题式(12)的KKT条件。内点法首先求解μ为固定值下障碍问题的近似解,然后减小μ继续求解,直到得到μ趋于0(趋近原问题的解)。在求解固定μ的障碍问题中,该算法应用了衰减牛顿法对原-对偶方程(13)迭代求解,通过式(13)简化的线性化形式构造搜索方向。采用线性搜索过滤法构造搜索步长,并提供二阶修正方法对步长进行校正。
本文采用的内点法求解器是由美国卡耐基梅隆大学AndreasWaechter等人[11]采用C++开发的软件包IPOPT(Interior Point OPTimizer)。
3 飞行器轨迹优化设计
3.1 飞行器数学模型
建立飞行器数学模型时做以下假设:(1)假设地球为均质不旋转圆球;(2)忽略附加哥氏力的影响;(3)采用指数大气模型和平方反比重力模型。基于上述假设建立如下动力学模型:

式中,m为飞行器质量;L,D分别为飞行器所受升力和阻力;H为飞行高度;γ为航迹角,ψ为航向角,北向为0°,东向为90°;θ为经度,φ为纬度;α为攻角,σ为倾侧角;g为重力加速度;Re为地球半径。气动力模型详细参见文献[7]。
目标函数为:

轨迹优化的目标函数为最大横程,计算过程中是对其等效的目标函数进行计算。

3.2 计算与分析
本文采用文献[4]中航天飞机的算例进行计算,并与文献中的计算结果进行比较,以验证算法的正确性。在进行自动微分和有限差分比较时,采用了ADOL-C中前向自动微分和中心有限差分。研究中采用的编译环境及计算机配置分别为:Visual 2008(SP1)和Intel(R)Core2 Duo CPU-E8400(3.0 GHz)处理器,内存2.00 G。
首先对研究中编制的直接配点法程序进行了验证,采用3.1中的模型及约束条件,对三种配点法方法进行了验证,离散点个数采用了逐步细化策略,微分方法采用自动微分。三种方法(Trapezoidal法(TRA)、Hermite-Simpson法(H-S)、Legendre伪谱法(LPS))计算结果与文献[7]计算结果的比较如表2所示,结果表明三种算法正确、可行,计算结果与文献中非常接近。图3~图6给出了其中一组优化计算的结果。

图3 高度、速度随时间变化曲线

表2 多种算法优化结果比较

图4 航迹角、航向角随时间变化曲线

图5 飞行轨迹地面投影(纬度-经度)

图6 攻角、倾侧角随时间变化曲线
为了比较自动微分和有限差分在轨迹优化中的应用,采用了不同离散方法(三种)进行计算,非线性规划的最大允许迭代次数为1 000,误差精度为5e-6;不进行网格细分的计算中离散节点个数为60。表3中给出了不进行网格细分的计算结果,结果表明采用ADM后,在收敛时间、稳定性方面得到了改善,同时可看到目标函数、约束函数的评价次数极大地减少,这对于目标及约束函数计算量大的问题极为有利(由于本文在气动力及大气模型计算时采用了拟合模型,降低了目标及约束的计算代价,所以在计算时间方面差别不太明显)。其中LPS中采用FDM计算方案达到最大迭代次数时没有获得满足精度要求的解,而采用ADM的方案获得了收敛解,这表明高精度的自动微分法有利于大规模非线性规划问题的收敛。

表3 ADM和FDM用于DCNLP轨迹优化结果
4 结束语
在基于直接配点的轨迹优化设计中,优化计算的效率受微分信息的影响很大,快速、精确地计算所需的微分信息对问题的求解至关重要。本文采用ADM进行微分计算,相对于传统FDM对目标函数、约束函数的计算次数大大减少,同时由于ADM可获得仅受机器精度限制、而与计算步长无关的高精度微分信息,使得非线性规划算法的收敛速度有所提高,这对飞行器的轨迹快速优化、快速生成具有重要意义,有着良好的应用前景。
[1] 颜力,陈小前,王振国.飞行器MDO中灵敏度计算的自动微分方法[J].国防科技大学学报,2006,28(2):13-16.
[2] 潘雷,谷良贤,龚春林.改进自动微分方法及其在飞行器气动外形优化中的应用[J].西北工业大学学报,2007,25(3):398-401.
[3] 蒋占四,吴义忠,蒋慧.敏度分析的数值方法比较研究[J].计算机与数字工程,2009,37(5):1-5.
[4] Kedem G.Automatic differentiation of computer programs[J].ACM Transactions on Mathematical Software,1980,6(2):150-165.
[5] 张春晖,程强,曹建文.针对C语言的自动微分系统及其应用[J].计算机应用研究,2009,26(1):155-159.
[6] Griewank A,Juedes D.ADOL-C:a package for the automatic differentiation of algorithms written in C/C++[J].ACM Transactions on Mathematical Software,1996,22(2):131-167.
[7] Betts J T.Practical methods for optimal control and estimation using nonlinear programming(2rd)[M].Philadelphia:SIAM Press,2010.
[8] Fahroo F,Ross IM.Advances in pseudospectralmethods for optimal control[R].AIAA 2008-7309,2008.
[9] Fahroo F,Ross I M.Direct trajectory optimization by a Chebyshev pseudospectral method[J].Journal of Guidance,Control,and Dynamics,2002,25(1):160-166.
[10] Garg D,Patterson M A,HagerW W,et al.An overview of three pseudospectralmethods for the numerical solution of optimal control problems[R].AAS-2009-332,2009.
[11] Walther Andrea,Griewank Andreas.On the implementation of a primal-dual interior point filter line search algorithm for large-scale nonlinear programming[J].Mathematical Programming,2006,106(1):25-57.

