基于ANSYS的500 kV电力变压器端部绝缘电场分析及结构优化

马爱清

(上海电力学院电力与自动化工程学院，上海 200090)

电力变压器是电力系统中的关键设备之一，也是电力系统中最昂贵和最重要的设备之一，其正常运行对整个电力系统的可靠运行起着非常关键的作用.在超高压电力变压器中，500 kV变压器在我国的应用较广泛，其绝缘设计的合理与否，对变压器运行的可靠性和经济性意义重大.

电力变压器主绝缘是变压器可靠运行的因素之一，电力变压器端部绝缘则是主绝缘的重要组成部分.电力变压器的端部绝缘不仅影响变压器运行的可靠性，同时也影响电力变压器的经济性——变压器的制造成本.本文利用ANSYS软件对某型号500 kV电力变压器的端部电场进行分析［1-7］，并在此基础上对其静电环的机构进行优化，得到了较好的绝缘结构.

1 计算模型的建立

变压器的主要部件是绕组和铁心(器身).绕组是变压器的电路，铁心是变压器的磁路.两者构成变压器的核心——电磁部分.除了电磁部分，还有油箱，绝缘装置，冷却装置，调压和保护装置等［8-11］.本文分析的是500 kV电力变压器高压绕组端部的电场，主要建立的是电磁部分的模型.电力变压器的绕组是套装在变压器的铁心柱上的，而铁心的结构左右对称，因此本文将高压绕组和低压绕组简化，取对称轴的一半来进行分析，同时也将低压绕组简化，主要建立高压绕组端部的模型.在ANSYS中建立的计算模型如图1所示.

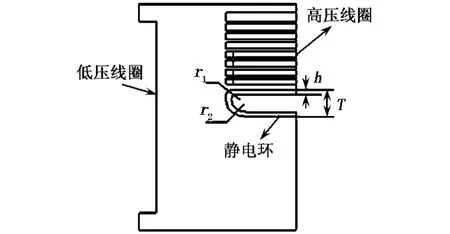
图1 500 kV电力变压器端部绕组示意

高压和低压绕组间绝缘距离为83 mm，静电环与金属压板距离为463 mm，h为0.5 mm，T为40 mm.需要说明的是，在计算过程中，需作如下假设:

(1)忽略引线对端部电场的影响;

(2)忽略端部成型绝缘件(角环、纸圈、隔板)等对电场的影响;

(3)认为绕组端部的铁轭最大级为垂直于铁心轴线的无穷大平面.

2 电力变压器电场的计算和分析

建立端部电场分析的计算模型时，需将油道简化;在设置材料属性时，主要考虑的材料为变压器油，变压器油的介电常数取2.3.网格剖分采用三角形剖分，剖分精度取0.03.得到有限元模型后，施加载荷，考虑本文分析的电力变压器电压等级为500 kV，边界条件分别为:高压绕组和静电环施加电压为500 kV，外壳和低压绕组为零.调用ANSYS的求解计算模块，得到了500 kV电力变压器的端部电位和电场分布见图2和图3.

图2 电位分布

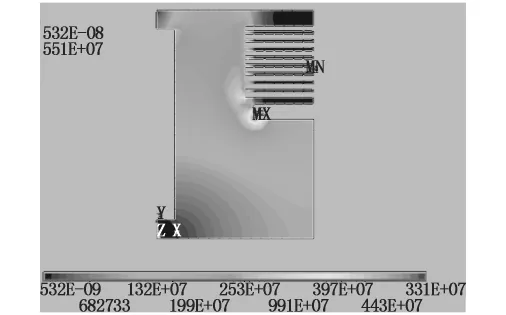
图3 电场分布

由图3可知，此时变压器油中电场强度的最大值Emax出现在静电环绝缘层表面，此时Emax=5.51 kV/mm.

高压绕组端部静电环的作用，一是改善与其相邻诸线段的雷电冲击电压分布;二是使绕组端部电场均匀.影响静电环表面场强的主要因素有静电环到铁轭或金属压板的距离、线圈间绝缘距离、静电环的曲率半径及绝缘层厚度，本文通过改变静电环的曲率半径来改变电场分布，以优化电力变压器结构.

3 静电环结构的优化

3.1 r1和r2不同值时电场分布计算

通过改变对应的曲率半径r1和r2，得到优化的静电环模型.

(1)增大r2来改变电场 将r2从0.02增大到0.035，r1保持不变，重新建立模型.经过剖分和施加边界条件，计算得到电场分布如图4所示.此时对应的电场强度最大值Emax=4.66 kV/mm.与图3相比，其最大场强值下降了15.4%.

图4 r2从0.02增大到0.035时的电场分布

(2)减小r2来改变电场 将r2从0.02减小到0.01，r1不变，重新建立模型.经过剖分和施加边界条件，计算得到电场分布如图5所示.此时对应的电场强度最大值Emax=5.39 kV/mm.与图3相比，最大场强值下降了2.2%，改变不太明显.

图5 r2从0.02减小到0.01时的电场分布

(3)增大r1来改变电场 将r1从0.008增大到0.012，r2不变，重新建立模型.经过剖分和施加边界条件，计算得到电场分布如图6所示.此时对应的电场强度最大值Emax=5.74 kV/mm.与图3相比，最大场强值增大了4.1%.

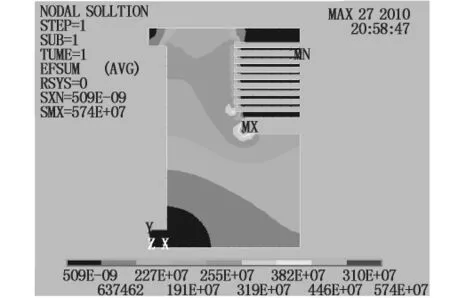
图6 r1从0.008增大到0.012时的电场分布

(4)减小r1来改变电场 将r1从0.008减小到0.004，r2不变，重新建立模型.经过剖分和施加边界条件，计算得到电场分布如图7所示.此时对应的电场强度最大值Emax=5.64 kV/mm.与图3相比，最大场强值增大了2.2%.

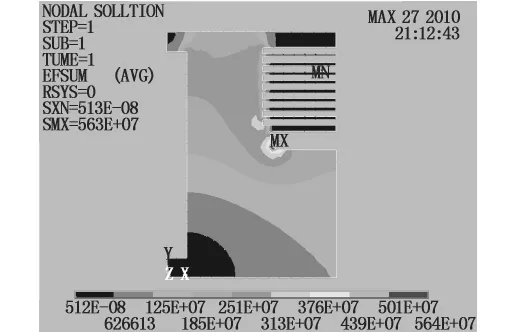
图7 r1从0.008减小到0.004时的电场分布

3.2 结果比较分析

对比得到的电场分布图和电场强度最大值Emax，发现增大和减小r2都能使电场的最大值变小，只是增大r2能使电场最大值更快地变小;增大和减小r1都使电场的最大值变大，只是减小r1使电场最大值更慢地变大.而静电环的宽度是一定的，对于变压器高压线圈端部绝缘结构而言，在设计中控制其最大场强小于起始放电场强是根本措施.为了使电场最大值尽可能小，应尽量增大r2和减小r1来使电场的最大值尽可能地变小.本文根据这样的原则建立了计算模型，此时r1=0.01，r2=0.03.求解计算得到的电场分布如图8所示.

由图8可知，此时对应的电场强度最大值Emax=5.01 kV/mm，比原电场的最大值(5.51 kV/mm)降低了9%，静电环模型由此得到了优化.

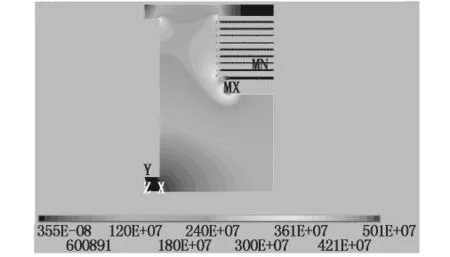
图8 r1=0.01和r2=0.03时的电场分布

4 结论

(1)利用有限元仿真软件ANSYS建立了电力变压器的二维计算模型，并在此基础上进行了有限元计算，得到了电力变压器高压端部绝缘的电场和电位分布图.

(2)通过改变静电环的曲率半径值，得到了最优的端部电场分布，优化了绝缘结构，为电力变压器端部绝缘静电环的设计提供了理论依据.

［1］刘传彝.电力变压器设计计算方法与实践［M］.沈阳:辽宁科技出版社，2002:15-18.

［2］路长柏，李新.超高压变压器线圈端部三维电场的计算问题［J］.变压器，1984，31(10):2-7.

［3］韦殿平，刘文里，勤格勒图，等.220 kV电力变压器端部绝缘传统与现行结构中电场的比较［J］.变压器，2009，46(10):6-10.

［4］刘建军，李岩.500 kV电力变压器主绝缘电场的有限元计算［J］.变压器，2008，45(9):1-4.

［5］刘建军.变压器主绝缘电场的解析计算与数值计算［J］.沈阳工程学院学报:自然科学版，2009，5(1):56-58.

［6］唐兴伦.ANSYS工程应用教程:热与电磁学篇［M］.北京:中国铁道出版社，2003:20-45.

［7］张波，盛和太.ANSYS有限元数值分析原理与工程应用［M］.北京:清华大学出版社，2005:35-43.

［8］尹克宁.变压器设计原理［M］.北京:中国电力出版社，2006:25-28.

［9］路长柏，郭振岩.电力变压器理论与计算［M］.沈阳:辽宁科学技术出版社，2007:42-48.

［10］刘建军.超高压电力变压器的绝缘计算［J］.电气技术，2008，8(5):43-46.

［11］陈曦东，陈昌渔.高电压工程［M］.北京:清华大学出版社，2003:5-20.