On the Equivalence of Short Sequences in Cyclic Groups of Prime Order
-, -
(Department of Mathematics,Dalian Maritime University,Dalian 116026,China)
1 Introduction
Amongnarbitrary integers one can choose several whose sum is divisible byn.In other words,each sequence of lengthnin the cyclic group of ordernhas a nonempty subsequence with sum zero.This article describes the sequences of length 2or 3in prime order cyclic group that fail the above property.
Here and henceforth,nis a fixed integer greater than 1,and the cyclic group of ordernis identified with the additive groupZZn=ZZ/nZZof integers modulon.A sequenceSinZZnis called a zero-sum sequence of the sum of its terms is the zero element ofZZn.A sequence is zero-sum free if it does not contain nonempty zero subsequences,and we callSaminimal zero-sum sequence if it is a zero-sum sequence and every proper subsequence is zero-sum free.
The object of study can be characterized in very simple terms.To be more specific,let us recall several standard notions.Ifgis an integer coprime ton,multiplication bygpreserves the zero sums in ZZnand does not introduce new ones.Hence asequenceα=(a1,…,ak)is zero-sum free if and only if the sequencegα=(ga1,…,gak)is zero-sum free,which motivates the following definition.
For sequencesαandβinZZn,we say thatαis equivalent toβand writeαβifβcan be obtained fromαthrough multiplication by an integer coprime tonand rearrangement of terms.Clearlyis an equivalent relation.
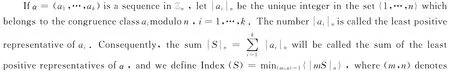
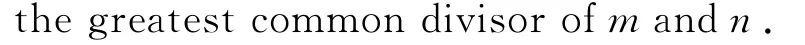
This statement reduces certain zero-sum problems in cyclic groups to the study of easy-todescribe positive integer sequences.
The question of considering equivalent sequences(see Chapter 5in[1])arose when the following problem was posed at Algebra conference in Marseille,France:
Letpbe a prime,whether each zero-sum sequenceSin cyclic groupZZpis equivalent to asequence whose sum of the least positive representatives isp?
The answer to this question is no (see Theorem 2of[2]),Subsequently,several authors[2-6]obtained ahuge variety of results on the equivalent sequences.
In this paper,we determine the upper bound of Index(S),whereSis asequence of length 2or 3 in prime order cyclic groupZZp.
2 The Main Results


[1]Geroldinger A and Halter-Koch F.Non-unique factorizations:algebraic,combinatorial and analytic theory[M].BocaRaton:Chapman & Hall/CRC,2006.
[2]Scott T.Chapman,Michael Freeze,and William W Smith.Minimal zero-sequences and the strong davenport constant[J].Discrete Math.,1999,203:271-277.
[3]Gao Weidong.Zero-sums in finite cyclic groups[J].INTEGERS:Electronic J.Combinatorial Number Theory 0(2000),#A12.
[4]Ponomarenko V,Minimal zero sequences of finite cyclic groups[J].INTEGERS:Electronic J.Combinatorial Number Theory 4(2004),#A24.
[5]Svetoslav Savchev,Fang Chen.Long zero-free sequences in finite cyclic groups[J].Discrete Math.,2007,307:2671-2679.
[6]Pingzhi Yuan.On the index of minimal zero-sum sequences over finite cyclic groups[J].J.Combinatorial Theory(series A),2007,114:1545-1551.

