马尾松球果各标志值与出种粒数回归分析补报

徐浩峰，韦蓉静，莫周卫

（1.都匀市马寨马尾松良种基地；2.黔南州林业科学研究所，贵州 都匀 558000）

通过多年的生产实践，马尾松种子出种率在2%～2.8%之间浮动。影响出种率的因素较多，如树木的营养状况、干旱或多雨、球果处理程度等方面，但很多因素不易测定和控制，我们想从较为直观易测的数据如球果的果重、果长、果径、种鳞数几个标志值来研究与出种粒数之间是否有线性关系。

1 试验材料、球果处理以及标志值的测定方法

1.1 试验材料

供试的马尾松球果在2011年采摘于贵州省都匀市马尾松良种基地1.5代种子园，分别从48个家系中选择无病虫害、无机械损伤、大小长短在该家系内适中的球果各10个，共选择球果480个做为总体。

1.2 球果处理以及标志值的测定方法

用电子天平对各球果重量称量，用游标卡尺测定果长、果径，人工计数种鳞数，并分别装入网袋按家系和序列编号。球果经石灰水浸泡48h后晾至不滴水，用烘箱烧烤至球果完全开放，种子自然脱落时取出去翅除杂质。本次测定的种子要求种粒饱满、无变质、无杂质，用电子天平称重并人工计数。

2 球果各标志值及数据统计

2.1 球果各标志值

从480组数据中随机抽取96组数据做为样本，抽取率为20%，抽取数据如下：

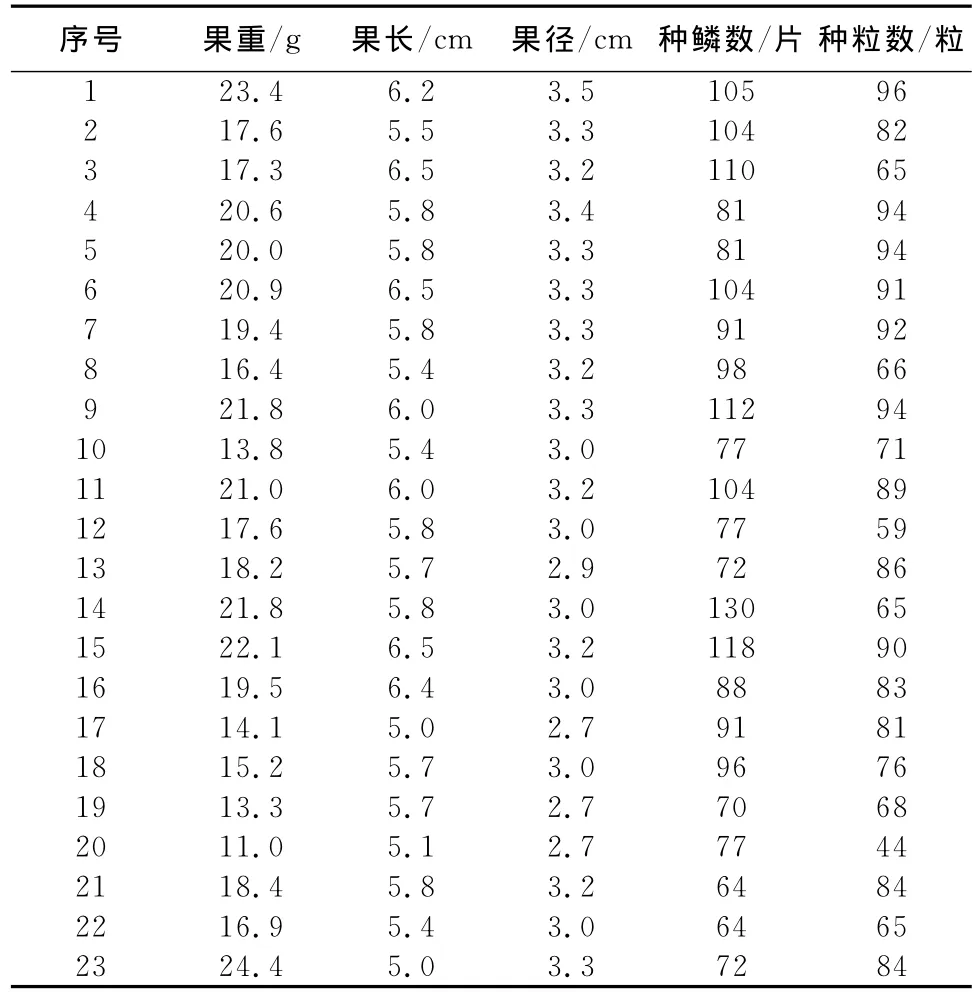
表1 马尾松球果与种子样本标志值测定

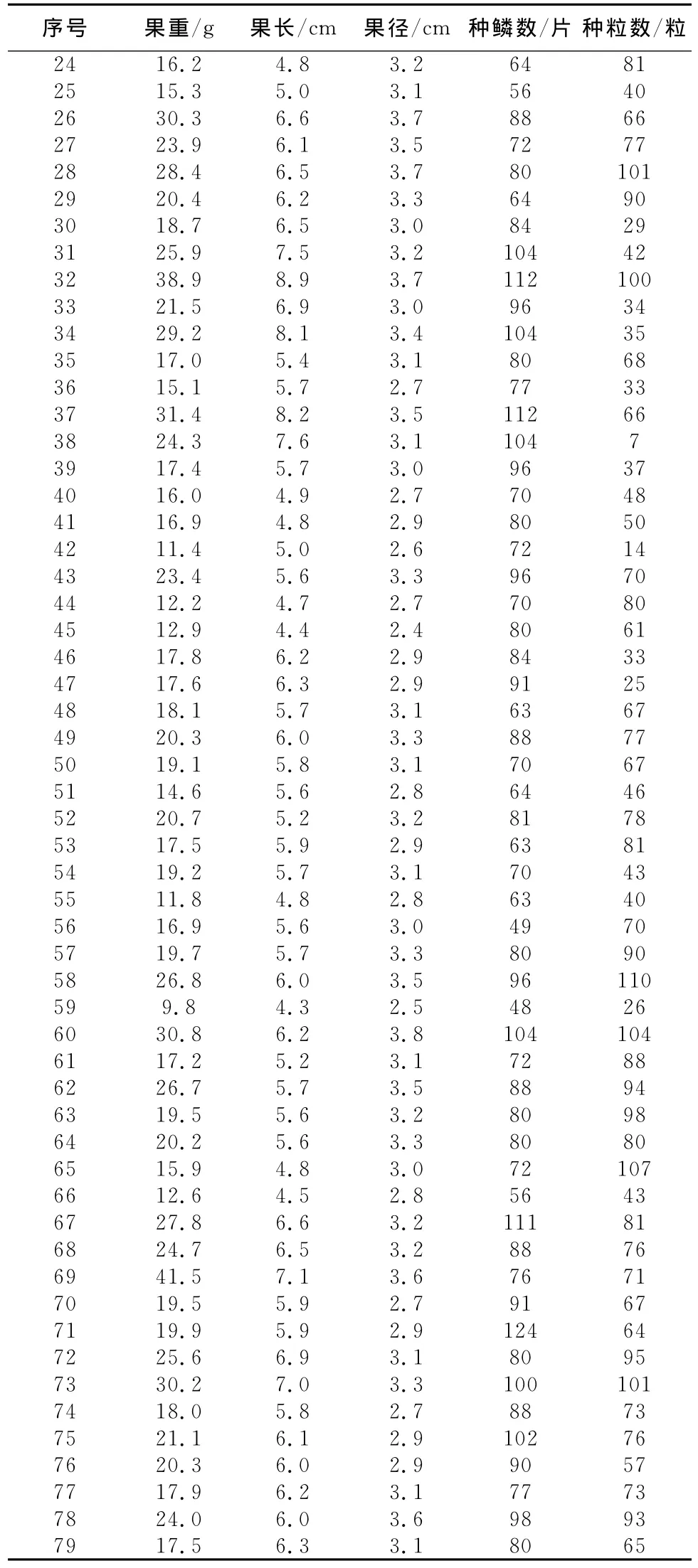
续表1

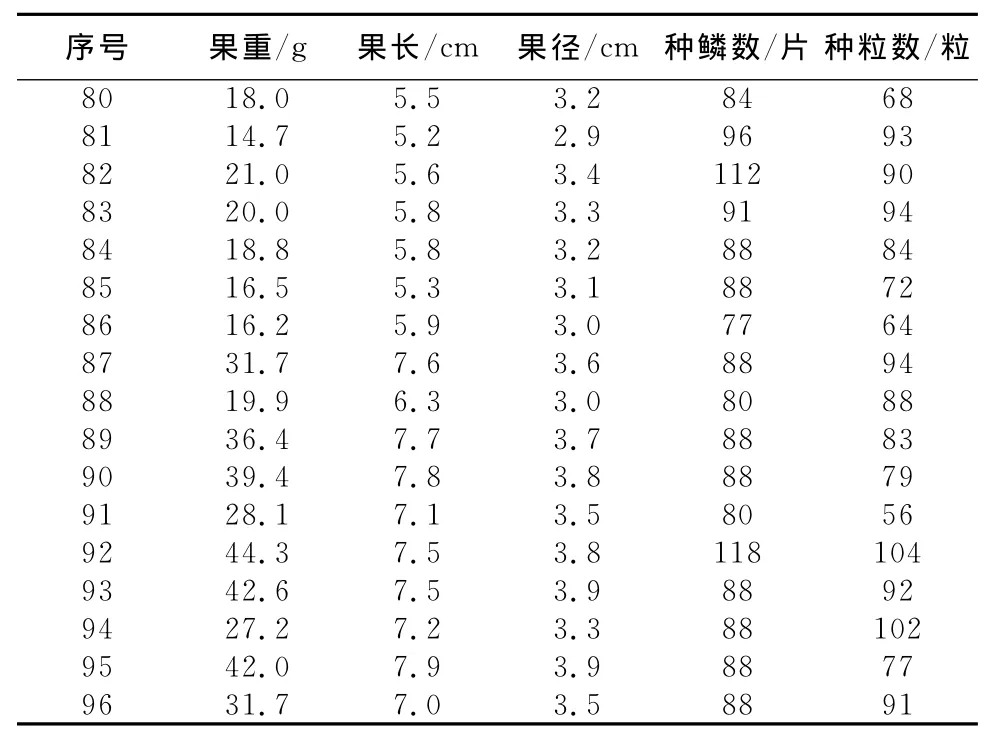
续表1

2.2 数据统计

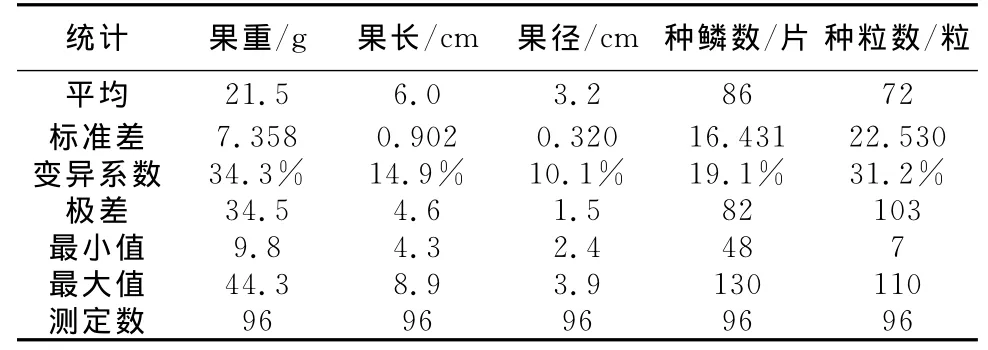
表2 样本标志值数据统计

通过表1的数据统计出表2，从表2得出样本各标志值的标准差分别为22.530＞16.431＞7.358＞0.902＞0.320；种粒数＞种鳞数＞果重＞果长＞果径，变异系数比较34.3%＞31.2%＞19.1%＞14.9%＞10.1%；果重＞种粒数＞种鳞数＞果长＞果径，从标准差和变异系数中得出数据分布分散程度最大的是种粒数、果重、种鳞数三项标志值，种粒数最大值103、最小值7、极差110；果重最大值44.3、最小值9.8、极差34.5；种鳞数最大值130、最小值48、极差130，但上述各标志值还不能得出与种粒数有无相关性的结论，还要通过以下回归分析来讨论。

3 回归分析与检验

通过把种粒数做为因变量，其它标志值做为自变量处理，组合成果重－种粒数、果长－种粒数、果径－种粒数、种鳞数－种粒数共四组数据进行一元线性回归与检验得出以下分析：

表3 一元回归统计表

表3中四组数据一元回归的相关系数与表值Ra比较得0.530＞0.379＞R0.01＝0.262＞0.227＞R0.05＝0.201＞0.147；即果径－种粒数R值＞果重－种粒数R值＞种鳞数－种粒数R值＞表值R0.05＞果长－种粒数R值，果径、果重与种粒数的直线回归相关系数极显著，种鳞数－种粒数的直线回归相关系数在表值R0.01和表值R0.05之间相关系数显著，它们所配合的样本直线回归方程有意义，果长－种粒数的直线回归相关系数小于表值R0.05，表明回归相关系数不显著，样本直线回归方 程无线性意义。

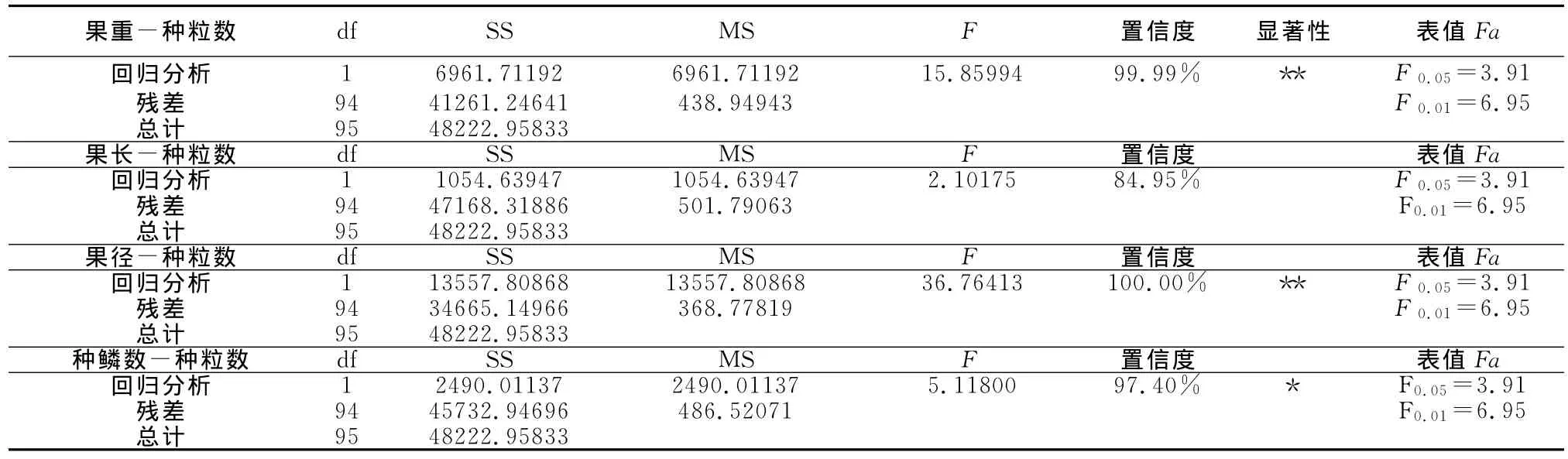
表4 方差分析表

表4方差分析表中通过方差分析得到F检验值，所得结论与回归统计表中的相关系数检验结果一致，直线回归关系果径－种粒数、果重－种粒数呈极显著水平，种鳞数－种粒数呈显著水平，直线回归方程有意义，果长－种粒数直线回归关系不显著，直线回归方程无意义。

表5 一元回归参数表

由表5一元回归参数表得出，三组数据回归方程的回归常数和回归系数，因表3、表4中果长－种粒数回归关系不显著，也就不讨论该项的回归参数，通过表5得回归方程如下：果重－种粒数回归方程：＝47.2975＋1.1634xi；果径－种粒数回归方程＝－45.9152＋37.3219xi；种鳞数 －种粒数回归方程＝45.5129＋0.3116xi

该三组回归方程对估计种粒数都有意义，前两个方程的置信度更高，能构成一元回归线性关系说明果重、果径、种鳞数对种粒数的正相关，三组数据越大种粒数也越大。但因变量（种粒数）与自变量（果重、果径、种鳞数）的是否有相互关系通过一元直线回归表现出一定的相关性，取得两变量之间相互关系的直线近似表达式，但只是一一对应的变量之间的关系式，较为片面不能反映多因素作用对某变量的影响情况，多变量的共同作用与因变量的相关性讨论应要用多元回归解决，我们还是用果重、果长、果径、种鳞数为自变量，种粒数为因变量进行分析，在分析过程中再删除t检验值不显著的自变量再进行回归分析，以免影响回归的显著性，分析如下：

对表6的回归参数表进行分析发现问题，截距、种鳞数的回归分析的t检验值（多元回归t值检验更具能反映该自变量的显著程度）达不到显著水平，对种鳞数做数据删除再进行回归分析，得出表7的结果，截距和果重也达不到t检验值的显著水平，对果重数据进行删除再进行回归分析，果长与果径相互作用对种粒数有极显著的线性回归关系，根据表8得出方程为＝－44.374－8.808xi（果长值）＋53.619xi（果径值），并且该方程有线性回归意义。

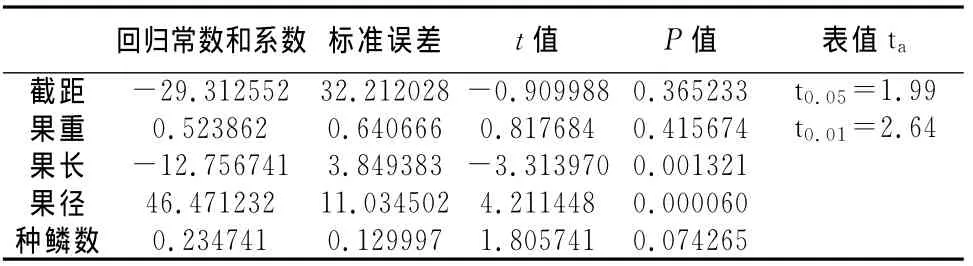
表6 回归参数表

表8 回归参数表

4 结论

4.1 通过多元回归分析，发现果长和果径直接影响这些标志值相互作用的因素。一元回归不能对总体标志值相互对出粒数作用进行全面分析，还是以多元回归分析更具有代表性。

4.2 对各标志值的分析，得出马尾松家系球果果长短与果径大小，呈显著线性相关，直接影响出种粒数。下一步要进行增加家系、营养状况、温度、积温、采摘时间等方面研究。

［1］ 毕庆雨.数理统计［M］.北京：中国林业出版社，1994.