基于磁场积分法和Tikhonov正则化的船舶固定磁场重建与分解技术

周国华，肖昌汉，刘大明，刘胜道

(海军工程大学 电气与信息工程学院，湖北 武汉430033)

0 引言

由于地磁场长期磁化作用和铁磁材料的磁滞效应，钢铁结构船舶周围不仅存在着感应磁场，而且还存在着固定磁场，这些磁场成为了磁性兵器的信号源，严重威胁着船舶生命力［1］。掌握船舶周围空间感应磁场和固定磁场分布是有效补偿感应磁场与消除固定磁场的必要前提。感应磁场属瞬时效应，其建模计算方法的研究相对较成熟［2－5］。固定磁场属积累效应，与舰艇复杂的磁化历史密切相关，鉴于船舶铁磁材料磁化历史的复杂性及其不可预知性，船舶固定磁场的建模计算一直是船舶磁隐身领域中的技术难题，因而文献［7－11］都结合各自应用背景对船舶固定磁场建模方法开展研究，但与实际应用阶段还存在一定差距。

一般而言，由于磁化历史的不可预知性，求解船舶固定磁场一般只能采用逆问题的思路，即依靠磁传感器测量得到部分磁场信息来反演计算船舶固定磁场。通常情况下，通过磁场测量只能获得固定磁场和感应磁性的合成磁场。因此，为实现船舶固定磁场的求解，必须分两步:首先通过正演技术将船舶的感应磁场分解出来;然后基于测得的磁场数据与计算得到的感应磁场值，建立固定磁场反演计算模型，通过求解反演模型以得到船舶固定磁场分布。按照该思路，本文提出了一种基于磁场积分法和Tikhonov 正则化方法的船舶固定磁场重建与分解技术，并设计了船模实验对方法有效性进行了检验。

1 船舶固定磁场重建与分解原理

如图1所示，不妨将钢铁结构的船舶离散为n个铁磁单元。假设某铁磁单元的磁化强度为M，则其在测量点P 处产生的磁感应强度B 可表示为M的函数

图1 船舶固定磁场计算原理示意图Fig.1 The sketch map of the remanent magnetic field calculation for naval vessels

采用磁场积分法进行求解时算子f［9］可表示为

为消除积分奇异性，算子f 的体积分形式在均匀磁化条件下可简化为相应的面积分形式［8，12］

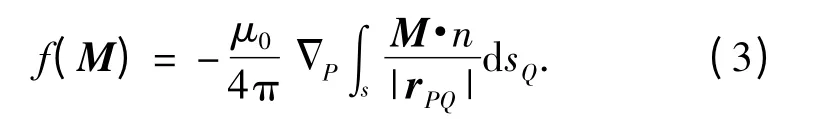
将铁磁单元内部总磁化强度M 表示为由外磁场引起的感应磁化强度Mind和由磁滞效应产生的剩余固定磁化强度Mrem之和，即M =Mind+Mrem。与其相对应，场点处磁场也可分为两部分，即由感应磁化强度产生的感应磁场Bind和由固定磁化强度产生的固定磁场Brem。通常情况下，感应磁化强度及其产生的感应磁场都可以通过正问题形式计算得到。与其它方法相比，磁场积分法具有只需剖分铁磁区、方程外不需另行考虑边界条件等优点，非常适合舰艇感应磁场等此类开域电磁场问题的建模计算，因而本文采用磁场积分法来计算舰艇感应磁场。但固定磁化强度及其产生的固定磁场，一般只能通过反问题形式进行反演计算。

在船舶外部空间m 个测量点处，基于磁场测量数据Bmea(已减去地磁场)和测量点处感应磁场计算值Bind，可建立如下固定磁场反演计算模型

式中:n 为船舶离散铁磁单元个数;Bx、By和Bz分别为B 的3 个分量;为第j 个铁磁单元内部固定磁化强度值;为第i个场点处的3分量磁场测量值;为第i 个场点处的感应磁场计算值;

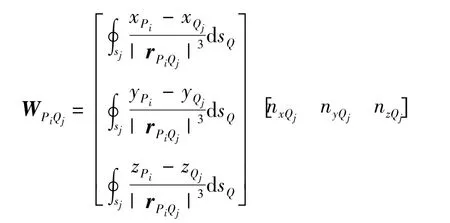
为第j 个铁磁单元对第i 个场点产生固定磁场的贡献矩阵，rPiQj表示第j 个铁磁单元Qj到第i 个场点Pi的矢径，［nxQjnyQjnzQj］表示第j 个铁磁单元单位外法线方向。(4)式写成矩阵形式可表示为AMrem=b，系数矩阵A 和列向量b 由(4)式易计算。求解该反演计算模型就可得到每个铁磁单元内部固定磁化强度分布，再根据式

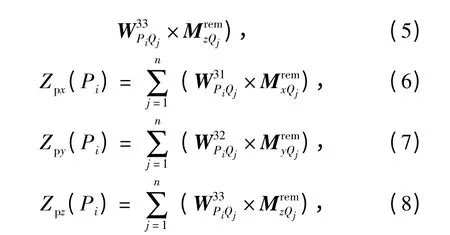
即可实现船舶固定磁场的重建与分解，其中Zp为固定磁场垂向分量总量、Zpx为纵向固定磁场垂向分量、Zpy为横向固定磁场垂向分量和Zpz为垂向固定磁场垂向分量。

然而，与其它应用领域的逆问题一样，由于测量信息的不足，反演计算模型(4)式常表现出很强的病态性。测量数据中较小的测量误差或感应磁场较小的计算误差都可能引起固定磁场反演计算结果的较大波动。处理病态逆问题而发展起来的正则化方法，为提高船舶固定磁场反演计算模型的稳定性提供了必要的技术支持。

2 固定磁场反演计算的实现

由上述固定磁场反演计算原理可以看出，实现船舶固定磁场建模计算主要包括3 方面内容:磁场测量、测量点处感应磁场的计算和固定磁场反演计算模型的求解。

2.1 磁场测量

在实际船舶磁场测量过程中，通常只能测得船舶下方空间某深度平面上若干点的磁场值，且多采用三线测量方式，即测量点分别位于船舶左舷、龙骨和右舷下方某深度直线上。为使船舶固定磁场计算具有通用性，采用三线测量方式作为船舶固定磁场计算中的磁场测量方案。

2.2 测量点处感应磁场的计算

以船舶各离散单元中心为场点，根据总场B 与磁化场Bm及外加场源B0的关系

及感应磁化强度与总场关系

再由(3)式则可得

式中:j =1，2，…，n;μr为铁磁物体的相对磁导率。求解方程(11)式，再结合Bind=f(Mind)即可实现船舶在测量点处感应磁场的计算。值得注意的是，在船舶磁性处理过程中，外加场源通常为地磁场，与强电流场相比，地磁场属弱磁场，因而船舶受地磁场磁化时磁化点位于线性磁化区，所以求解方程(11)式时不需要进行反复迭代，可视船舶铁磁材料相对磁导率为常数，从而达到简化计算的目的。

2.3 固定磁场反演计算模型的正则化求解

随着逆问题模型在各实际工程领域的出现，病态逆问题的求解方法也得到了深入研究，正则化方法能够有效抑制数据误差对病态逆问题计算结果的影响［13－16］。常用的正则化方法有Tikhonov 正则化方法、截断奇异值分解法和迭代正则化方法等，鉴于Tikhonov 正则化方法的理论最为成熟且应用最为广泛，本文将其用来求解船舶固定磁场反演模型。

将系数矩阵A 进行奇异值分解A=USVT，U 及V 为正交矩阵，S 为A 的奇异值组成的对角阵。且令b=btrue+Δb，则(4)式解可表示为

式中:ui为正交矩阵U 的第i 列向量;vi为正交矩阵V 的第i 列向量;r 为奇异值个数;si为第i 个奇异值;btrue为磁场测量数据与感应磁场计算值之差的真值列向量;Δb 为磁场测量数据与感应磁场计算值之差所带有的误差列向量。不难发现，较小的奇异值对误差具有放大作用，从而引起了解的不稳定。一般来讲，逆问题不适定程度越高，这种放大作用越明显，微小的测量误差也可能引起解的较大波动。为抑制小奇异值对误差的放大作用，Tikhonov 正则化方法的基本思想是在(12)式解系数中加一滤波因子，即

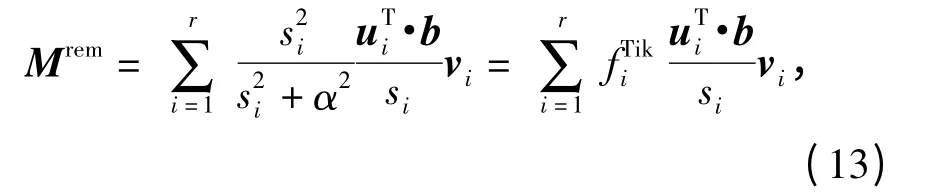
式中:α 为正则化参数;fTiki为滤波因子。不难看出，若取α=0，则所得解即为最小二乘解。α 越大则越强调解的稳定性和平滑性，α 越小则越强调解与测量数据的吻合程度，因而正则化参数的选择影响着解的性能。目前主要可根据Morozov 原理、广义交叉校验和L 曲线法等来确定正则化参数。为方便，本文使用L 曲线法来选择磁场逆问题模型中所需的正则化参数，L 曲线是指在xy 平面上，所有点(log‖AMrem－b‖，log‖Mrem‖)构成的一条单调递减且成L 形状的曲线。通常情况下，L 曲线上曲率最大的点对应着最佳的正则化参数，因而求取L曲线的最大曲率点即可得到相应的正则化参数。

3 磁性船模固定磁场重建与分解实例

以一艘水面舰艇按一定比例缩小的磁性船模为对象，长度为235 cm、宽度为29 cm，相对磁导率100～200，并通过测量得到了该船模的型体结构数据。固定磁场建模计算中取平均相对误差ARE 作为误差评估指标，其定义为

3.1 船模磁场的测量

如图2所示，在无磁实验室(地磁场水平分量大小为34 200 nT，垂向分量大小为34 500 nT)进行船模磁场测量工作。取9 个3 分量磁通门传感器且分3 个测量深度放置，同一深度3 个磁传感器分别置于船模左舷、龙骨和右舷下方，且所在直线与船模运动方向相垂直。考虑到实际船舶磁场测量时一般只能测得垂向分量，因而仅采用磁场测量数据中的垂向分量数据进行计算。

图2 磁性船模磁场测量示意图及测量点阵分布图Fig.2 The sketch map of the magnetic field measurement of the mock up and the measurement points distribution

在船模坐标系下，通过测量分别得到了船模在北航向时3 个测量平面z1=11.9 cm，z2=23.9 cm 和z3=36.1 cm 上41 ×3 点阵上的磁场值，x 方向41 个测量点、间距10 cm、坐标范围为［－200 cm，200 cm］，y方向3 个测量点、间距15 cm、坐标范围为［－15 cm，15 cm］.为解算船模感应磁场和固定磁场测量值，以与计算值作比较，调转船模航向采用相同的方法测量得到了船模南航向时在上述场点处产生的磁场值，感应磁场和固定磁场测量值解算方法可参考文献［17］。

3.2 船模感应磁场的计算

为实现固定磁场重建，首先必须计算船舶感应磁场。在船模北航向时测得的磁场数据垂向分量中所包含的感应磁场主要为由地磁场纵向磁化作用产生的纵向感应磁场垂向分量Zix和由地磁场垂向磁化作用产生的垂向感应磁场垂向分量Ziz.为实现Zix和Ziz的计算，在兼顾计算精度和计算时间的情况下，采用TrueGrid 软件将该水面舰艇磁性船模离散为315 个四边形壳体单元，如图3所示。

图3 船模四边形壳体网格剖分示意图Fig.3 Mesh of the mock up with quadrangular shell elements

基于船模网格离散数据，以正问题形式计算得到了平面z2上场点处的Zix和Ziz，并将Zix计算值与测量值进行了比较，见图4(图中磁场值进行了归一化处理，即用任一点的磁场值与所有磁场值中的最大绝对值之比作为该点的磁场值)。由图可见二者具有很好的吻合度，平均相对误差为3.29%。图5给出了船模在地磁场垂向分量垂向磁化时在平面z2上场点处Ziz的分布曲线。

图4 平面z2上Zix计算值与测量值对比曲线Fig.4 The comparison of the calculated Zix and the measured one on plane z2

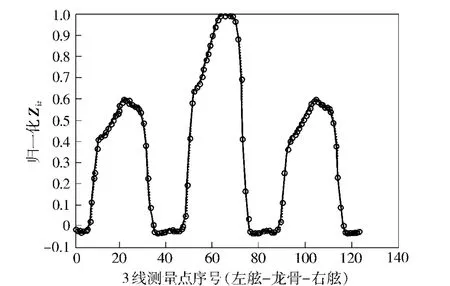
图5 平面z2上Ziz计算值曲线Fig.5 The comparison of the calculated Ziz on plane z2

3.3 船模固定磁场的重建与分解

在求得上述感应磁场后，基于船模北航向平面z2上场点处的磁场测量数据垂向分量值Bz2z可建立如下固定磁场反演计算模型

式中Az为(4)式系数矩阵A 中相应的垂向分量。考虑到Zpy一般具有在龙骨下场点处为0 和在左右舷下场点处同值异号的特点，故将该特性形成的方程作为上述船模固定磁场逆问题求解的辅助方程一并进行求解。

求解过程中发现，模型(15)式系数矩阵条件数为1.04 ×1012，固定磁场逆问题模型严重病态。为克服病态的影响，采用Tikhonov 正则化方法对其进行了求解，并用L 曲线法对正则化参数进行了选取α=1.04 ×10－6，图6给出了正则化选取的L 曲线。基于所选取的正则化参数求解得到了船模各离散单元的固定磁化强度，并由其计算得到了平面z1与平面z3上场点处Zp分布及平面z2上Zpy分布，与测量值比较结果见图7～图9.

图6 正则化选取的L 曲线Fig.6 L curve of the choice of the regularization parameter

图7 平面z1上Zp计算值与测量值对比曲线Fig.7 The comparison of the calculated Zp and the measured one on plane z1

由图7和图8可以看出，平面z1和平面z3上船舶固定磁场Zp计算值与测量值都具有很好的一致性，平均相对误差分别为2.53%和1.24%。

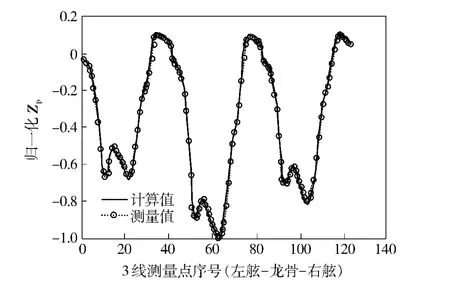
图8 平面z3上Zp计算值与测量值对比曲线Fig.8 The comparison of the calculated Zp and the measured one on plane z3

图9 平面z2上Zpy计算值与测量值对比曲线(左舷)Fig.9 The comparison of the calculated Zpy and the measured one on plane z2(at the larboard points)

由图9可知，平面z2上船舶固定磁场Zpy计算值与测量值具有相同的趋势，平均相对误差为6.13%，在某些场点处二者存在较大差异的主要原因是:与船舶固定磁场Zp相比，Zpy分量较小，因而在一定测量误差条件下根据磁场测量数据解算Zpy时会带有较大的误差。

从船模固定磁场的重建与分解过程可以看出，误差来源主要为:1)量取的船模型体、结构数据与实际船模存在一定的差异;2)固定磁场逆问题模型所用磁场测量数据中带有的测量误差与测量点处感应磁场计算误差。

为进一步考核文中算法有效性，采用文献［11］中基于等效磁源法的船舶固定磁性分解方法对上述算例进行了求解，固定磁场Zpy平均相对误差为8.34%。从基于等效磁源法的船舶固定磁性计算方法和基于磁场积分法和Tikhonov 正则化方法的船舶固定磁性计算方法的整个计算过程和比对结果，可以看出:

1)文中算法比基于等效磁源法的固定磁场计算精度略高，二者计算的平均测量误差均可小于10%;

2)基于等效磁源法的固定磁场建模方法需较多先验知识，当船舶磁场比较复杂时，受先验知识影响较大，从而导致模型通用性、稳定性降低，而文中算法可避免此弊端;

3)基于等效磁源法的固定磁场建模方法需采用遗传算法搜索等效磁源的位置参数，不适当的约束条件会使得搜索效率较低，从而影响固定磁场计算效率，而文中算法基于固定磁性产生的机理，并不涉及磁源优化搜索，因而计算效率较高。因此，与基于等效磁源法的船舶固定磁性建模方法相比，基于磁场积分法和Tikhonov 正则化方法的船舶固定磁性计算方法具有一定的优势。

4 结论

本文基于磁场积分法和Tikhonov 正则化方法实现了船舶固定磁场的重建与分解，为船舶磁性处理时船舶固定磁场计算与分解提供了一条新途径。在相同的计算精度下，文中算法具有更好的计算效率和稳定性。船舶固定磁场重建与分解实例验证了该方法的有效性，有一定工程实用意义。

References)

［1］ Holmes J J.Reduction of a ship’s magnetic field signatures［M］.Maryland:Morgan ＆ Claypool Publishers，2008:1－3.

［2］ 翁行泰，曹梅芬.潜艇感应磁场的三维有限元法计算研究［J］.上海交通大学学报，1994，28(5):69－76.WENG Xing－tai，CAO Mei－fen.A research on the calculation of the induced magnetic field of a submarine［J］.Journal of Shanghai Jiaotong University，1994，28(5):69－76.(in Chinese)

［3］ 郭成豹，何明，周耀忠.积分方程法计算舰船感应磁场［J］.海军工程大学学报，2001，13(6):71－74.GUO Cheng－bao，HE Ming，ZHOU Yao－zhong.Calculation of induced magnetic fields of ships by integral equation method［J］.Journal of Naval University of Engineering，2001，13(6):71－74.(in Chinese)

［4］ Chadebec O，Coulomb J L，Leconte V，et al.Modeling of static magnetic anomaly created by iron plates［J］.IEEE Transaction on Magnetics，2000，36(4):667－671.

［5］ 郭成豹，刘大明，肖昌汉，等.船载活动设备磁场建模分析研究［J］.兵工学报，2009，30(2):196－200.GUO Cheng－bao，LIU Da－ming，XIAO Chang－han，et al.Magnetic field modeling of shipborne moving equipment［J］.Acta Armamentii，2009，30(2):196－200.(in Chinese)

［6］ 王玉梅，于乃功.舰船周围空间固定磁场建模方法研究［J］.潍坊高等专科学校学报，1998，(4):42－49.WANG Yu－mei，YU Nai－gong.Study on the method of the ship permanent magnetic field modeling［J］.Journal of Weifang Higher Academy，1998，(4):42－49.(in Chinese)

［7］ 王学军，夏润海，王开颜，等.回归分析法在舰船周围空间固定磁场建模中的应用［J］.数学的实践与认识，2001，31(4):430－434.WANG Xue－jun，XIA Run－hai，WANG Kai－yan，et al.Application of recursive method in vessel’s surrounding permanent magnetism product modeling［J］.Mathematics in Practice and theory，2001，31(4):430－434.(in Chinese)

［8］ Chadebec O，Coulomb J L，Bongiraud J，et al.Recent improvements for solving inverse magnetostatic problem applied to thin shells［J］.IEEE Transactions on Magnetics，2002，38(2):1005－1008.

［9］ Chadebec O，Coulomb J L，Cauffet G，et al.How to well pose a magnetization identification problem［J］.IEEE Transactions on Magnetics，2003，39(3):1634－1637.

［10］ Vuillermet Y，Chadebec O，Coulomb J L，et al.Scalar potential formulation and Inverse problem applied to thin magnetic sheets［J］.IEEE Transactions on Magnetics，2008，44(6):1054－1057.

［11］ 高俊吉，刘大明，姚琼荟.舰船固定磁性分解方法研究［J］.哈尔滨工程大学学报，2007，28(10):1164－1170.GAO Jun－ji，LIU Da－ming，YAO Qiong－hui.Study of the separation to the permanent magnetic field of ship［J］.Journal of Harbin Engineering University，2007，28(10):1164－1170.(in Chinese)

［12］ 樊明武，颜威利.电磁场积分方程法［M］.北京:机械工业出版社，1988:11－19.FAN Ming－wu，YAN Wei－li.Integral equation method of the electromagnetic field［M］.Beijing:China Machine Press，1988:11－19.(in Chinese)

［13］ Hansen P C.Rank－deficient and discrete ill－posed problems:numerical aspects of linear inversion［M］.Philadelphia:SIAM，1998:45－66.

［14］ 姚姚.地球物理反演基本理论与应用方法［M］.武汉:中国地质大学出版社，2002:14－69.YAO Yao.Basic theory and application methods in geophysical inverse problem［M］.Wuhan:China University of Geo Sciences Press，2002:14－69.(in Chinese)

［15］ 黄卡玛，赵翔.电磁场中的逆问题及应用［M］.北京:科学出版社，2005:13－51.HUANG Ka－ma，ZHAO Xiang.Electromagnetic inverse problems and applications［M］.Beijing:Science Press，2005:13－51.(in Chinese)

［16］ 王彦飞.反演问题的计算方法及其应用［M］.北京:高等教育出版社，2007:33－95.WANG Yan－fei.Computational methods for inverse problems and their applications［M］.Beijing:Higher Education Press，2007:33－95.(in Chinese)

［17］ 张连魁.舰船磁场分析—临时线圈消磁［M］.武汉:海军工程学院，1991:74－76.ZHANG Lian－kui.The analysis of the magnetic field and deperming of ships［M］.Wuhan:Naval University of Engineering，1991:74－76.(in Chinese)