中高压喷嘴集成优化数值仿真
凌 轩,王 毅,黄伟锋
(仲恺农业工程学院机电工程学院,广东 广州 510225)
喷嘴是水射流技术应用中获得高能量利用率的关键因素之一,对射流质量有重要影响。喷嘴结构是指喷嘴的流道形状与几何尺寸,喷嘴的流动特性即水力特性是指它所形成的射流扩散角的大小、等速核长度以及喷嘴流量系数的大小。喷嘴结构与射流性能之间的关系,直接影响着反推力的大小和推进效率。在加工喷嘴试件进行试验之前,必须对不同结构尺寸的喷嘴进行理论分析和仿真研究,以便对需要加工的喷嘴试件的形状和尺寸提供理论依据。
在传统得CFD产品前期设计中,一般先对产品进行初始化建模,运行CFD仿真程序,分析设计结果,再改变设计参数,运行仿真程序,再分析设计结果,如此不断循环反复,最后找出一组最佳参数,使得产品的性能等指标达到最优。这种不断重复建立模型,运行仿真程序,分析结果的过程不仅浪费了大量的时间,而且在有多个设计变量的情况下工作量非常大有时甚至是不可行的。另一方面,传统的CFD软件一般优化功能比较弱,而且从商业保密的角度考虑很少公开源代码,这使的我们要加入自己的优化算法变的非常困难。为了克服以上不足,近年来提出了CFD集成优化算法。算法的核心是把CFD建模和运算工具看成一个黑匣子,只利用它们的设计参数和输出结果而不关心它们是怎样运算的,然后可加入自己的优化算法自动得到想要得结果。
本文应用遗传算法,对喷嘴的CFD集成优化的方法进行研究。喷嘴集成优化设计过程,可分为四个步骤,主要步骤为:参数化建模、几何集成自动划分网格、非结构CFD运算仿真、集成优化设计。本例子参数化建模和自动划分网格由专用前处理软件包Gambit完成。Gambit主要功能包括三个方面:构造几何模型、划分网格和指定边界。它提供结构网格、非结构网格和混合网格等多种类型得网格,并最终生成包含有边界信息得网格文件。选择Fluent作为CFD运算仿真的求解器,因为它具有很强的求解非结构自适应网格能力。最后,通过命令行方式调用Gambit和Fluent提供的接口,对它们进行集成优化。优化算法可根据不同问题的要求选用不同的优化算法。由于遗传算法GA具有很强的非线性搜索能力,这里选用遗传算法算法作为本例子的优化算法。例子取Gambit的的输入和Fluent的输出作为输入变量和输出变量,在一定范围内不断改变变量值自动进行优化运算最终得到优化结果。
1 物理建模及流场分析
1.1 物理模型及网格划分
柱形喷嘴模型如图1所示。AB、BC、CD、DE、EF为固壁(Wall),AJ为速度进口(Velocity-inlet),FG、GH、HI为压力出口(Pressure-outlet),IJ为对称轴(Axis)。柱形喷嘴的特征尺寸为柱形喷嘴的孔径d1(以IJ为对称轴,CD为母线的圆柱面的底面直径)和出口长度L(线段CD的长度)。
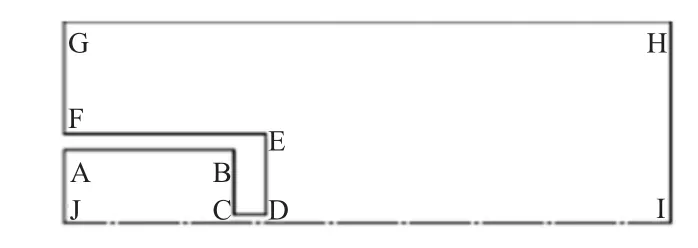
图1 圆柱喷嘴网格模型
柱形喷嘴模型的网格划分如图2所示。AB下方以及EF右延长线下方的区域为射流形成的区域,因此须使用密网格;该区域的网格密度因位置的不同而有所变化,如CD下方的网格最密,靠近AJ和HI的部分网格较疏,故该区域只能使用三角形单元进行网格划分;在建立模型时EF的长度不变,可取整数值,故EF及其右延长线上方的区域可使用很疏的四边形网格。完成网格划分后,再进行边界类型的设置。将 AB、BC、CD、DE、EF 设为固壁(Wall),AJ设为速度进口 (Velocity-inlet),FG、GH、HI设为压力出口(Pressure-outlet),IJ设为对称轴(Axis)。

图2 柱形喷嘴模型网格划分
高质量的网格划分是提高数值模拟精度的关键。一般要求流场中的网格要保持一定的正交性(尽可能达到90°)。在Gambit里检查网格质量。从检测结果可以看出,在0~0.2之间的网格占了95%,入口处的网格精度也不错,能够保证求解能很快收敛。
1.2 CFD计算
计算采用二阶迎风差分格式,基于微元中心有限体积法离散连续相控制方程,通过SIMPLE算法求解压力速度耦合,湍流模型采用标准k-e模型。收敛判据为流场迭代的残差R<=10-5。
1.3 计算流场设置自动化
在流体的数值模拟计算中需要设置较为复杂繁琐的边界条件和其他设置,手动设置步骤繁琐,工作量大,重复劳动多,效率低,本文应用了Gambit和Fluent自带的journal文件以及command自动导入网格文件,设置边界条件及约束以及计算步数,可以大大减少设置时间,增加效率。
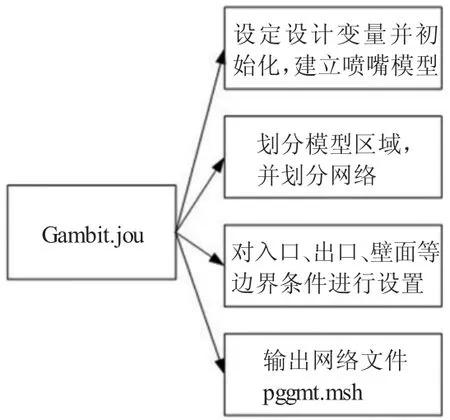
图3 Gambit.jou的内容
应用Gambit的命令行功能,如图2所示,可对自旋双喷嘴进行参数化建模和边界设置,最后输出msh网格文件。
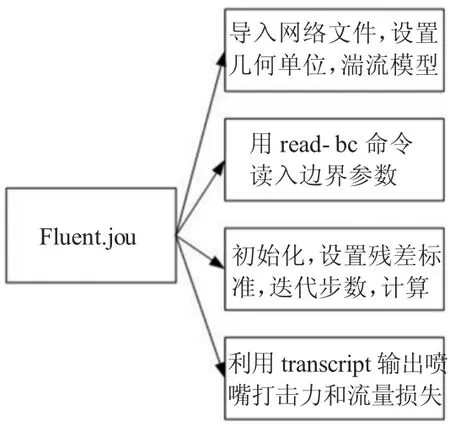
图4 Fluent.jou的内容
应用Fluent提供的command和transcript功能,如图3所示,对边界条件、湍流模型残差等参数进行设置,最后输出包含喷嘴打击力和流量损失的transout文件。
2 集成优化
2.1 目标函数和约束条件
中高压喷嘴射流打击力主要技术参数有压力、流量、功率、喷射直径及喷管的流场形状等。一般来说压力越大,直径越大,喷管的打击力就越大,清洗的效果就越好。但这还有一个功率匹配的问题,喷嘴直径越大,所需的流量也越大,功率也越大。结合本课题的实际,这里把喷嘴直径、喷嘴长度、喷嘴内锥角作为设计变量。喷嘴直径取1mm至3 mm,喷嘴长度4 mm至6 mm,喷嘴内锥角20度至30度之间。
目标函数综合考虑了流量损失和射流打击力的关系,权衡它们之间的关系。
2.2 改进的CFD集成优化算法
CFD集成优化过程如图4所示。
这里采用了遗传算法GA和序列二次规划SQP相结合的优化方法。遗传算法可以在计算的初始阶段扩大搜索空间,不会导致计算陷入局部最优的困境;然后用数值算法序列二次规划法,可加快收敛速度求出最优解。
由于无论是何种遗传算法,每代都会遇到相同的个体。而且一般cfd运算时间较长,如何对遗传算法控制,加快收敛速度缩短计算时间是一个值得考虑的问题。我这里采用的方法对每个设计变量都进行判断,如果某一个设计变量的两个解的绝对差大于一个小量,如1e-2,认为两者不等了;反之,每个绝对差小于1e-2,则认为相同或非常接近,就从数据库直接给出计算结果。实践证明,采用此方法后,可大大加快收敛速度。
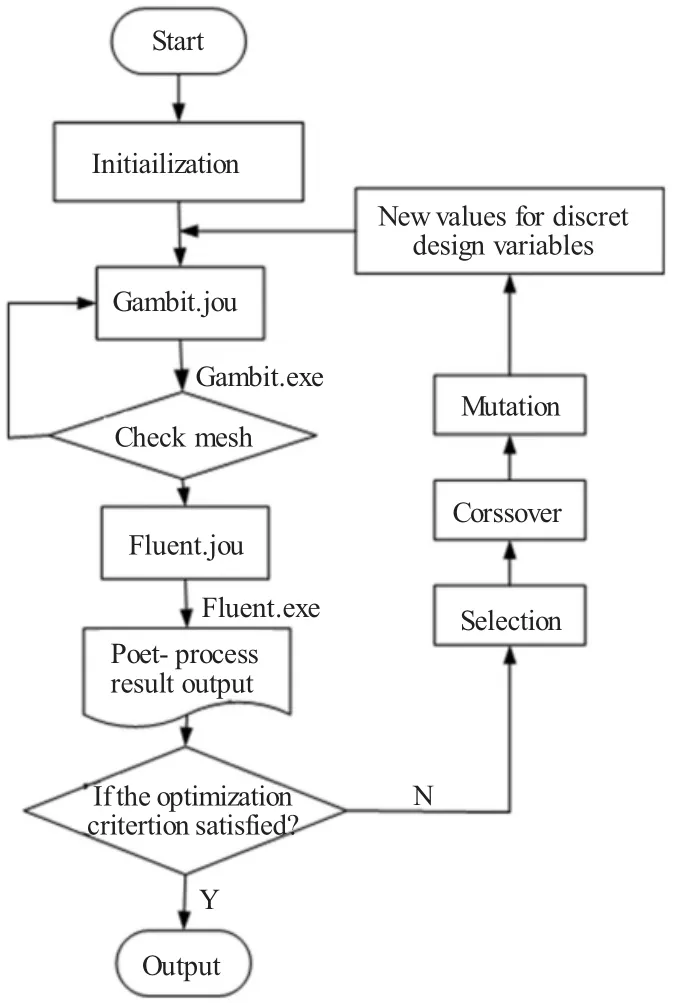
图5 CFD集成优化过程
3 集成优化结果
给定射流压力30MPa,对喷嘴直径径、喷嘴长度、内锥角进行优化,优化结果如下(图6~图8)。
图5与图6分别是在其他参数不变的情况下,喷嘴直径D、收缩角和打击力的关系。从仿真结果可以看出喷嘴半径越大,射流速度越小,而打击力就越大。图8是在其他参数不变的情况下,喷嘴长度L和打击力的关系。仿真结果表明喷嘴长度对打击力的影响不大,趋势是喷嘴长度越长,打击力有缓慢下降趋势。
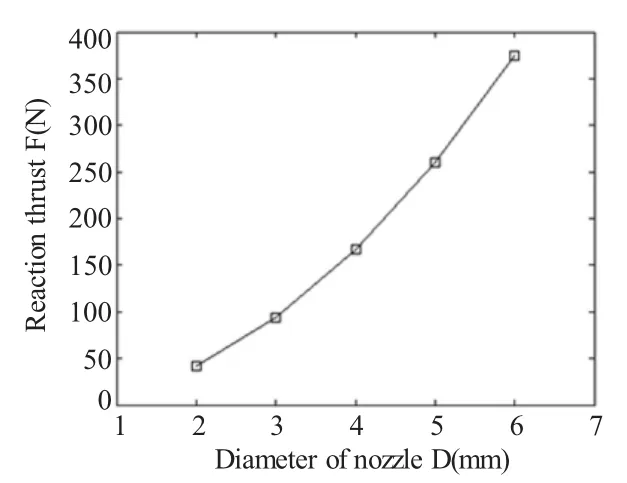
图6 喷嘴直径D与打击力关系
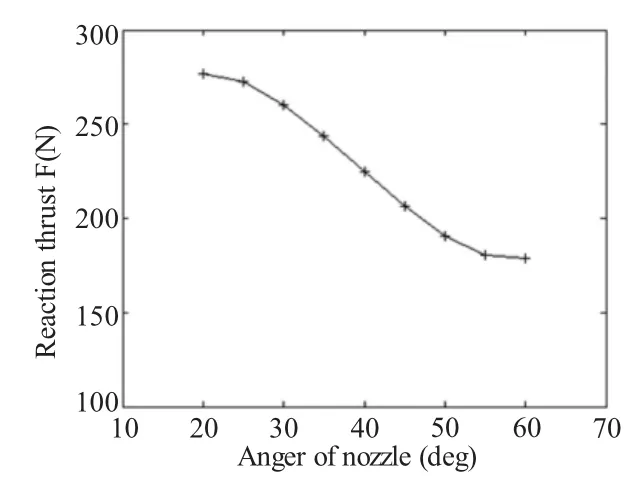
图7 喷嘴收缩角与打击力关系
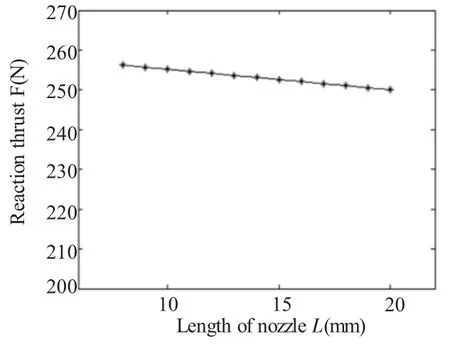
图8 喷嘴长度L与打击力关系
图9为喷嘴优化结果。图10是以喷嘴半径、喷嘴长度、内锥角为设计变量条件下,运行次数和射流打击力关系历史曲线。由于采用了加快收敛速度的算法,这里程序只运行了26次就已经收敛,得到最佳打击力约为223牛。
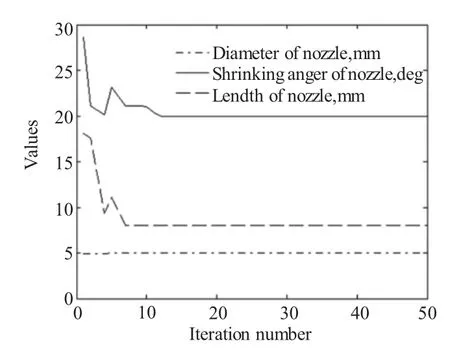
图9 喷嘴参数优化结果
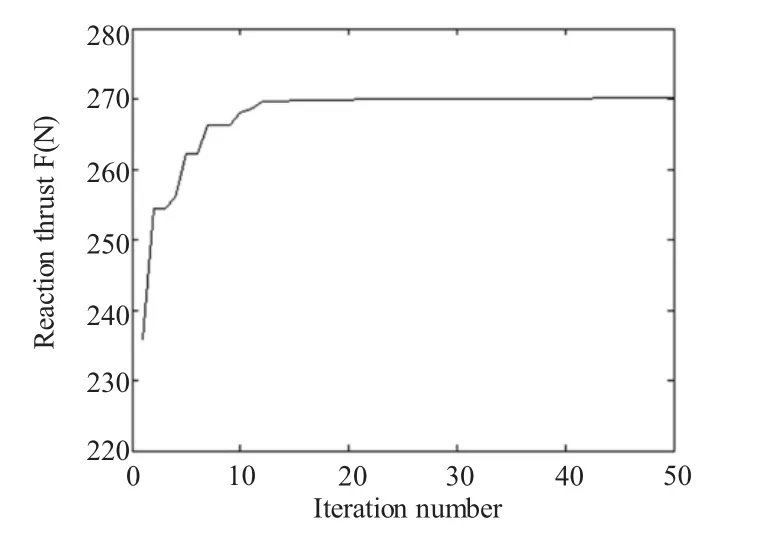
图10 喷嘴优化历史曲线
通过对喷嘴内锥角、直径、长度等参数进行总体优化,提高了它的打击能力(见表1),并且流场的性能也得到了改善。

表1 优化前后性能参数比较
4 结论
本文以中高压喷嘴作为例子,采用基于遗传算法的集成CFD优化方法,对喷嘴进行了优化设计。从仿真结果可以看出,喷嘴得打击能力和流场特性都有了很大得提高。集成优化算法对于产品优化设计是一个强有力的工具。优化过程是通过集成gambit参数化建模、自动划分网格接口和fluent运算器接口的方法实现的。这种集成CFD软件优化方法大大节省了设计时间和效率,也可用于集成其它CAD应用软件最终用在多学科优化设计中,有非常广阔的应用前景。
[1]Rahman MM,Rahman MK.An integrated model for multiobjective design optimization of hydraulic fracturing[J].Journal of Petroleum Science and Engineering.Volume:31,Issue:1,October,2001,pp.41-62.
[2]Araujo A,Lima JLFC.Anintegrated design strategy for flow injection analysis based on the coupling of mathematical modelling and optimization algorithms[J].Analytica Chimica Acta Volume:310,Issue:2,June 30,1995,pp.289-296.
[3]Gruhn Patrick,Henckels Andress.Flap contour optimization for highly integrated SERN nozzles[J].Aerospace Science and Technology Volume:4,Issue:8,November,2000,pp.555-565.
[4]薛胜雄等.高压水射流技术与应用[M].北京:机械工业出版社,1998.
[5]李根生,沈忠厚等.自动旋转喷嘴的理论研究[J].石油学报,1995:185~189.
[6]Guoqin Huang,Xiaohui Li,Yuquan Zhu,et al.,Experimental Studyin Reaction Thrust Characteristics ofWater Jet for Conical nozzle,China Ocean Engineering 12(2009)669-678.

