基于等值回路方程的变压器保护判据的研究

王 媛，焦彦军，金 晶，马叶芝

0 引言

变压器是电力系统中的重要输变电设备，它的故障将对供电可靠性和系统安全运行带来严重的影响，因此研究性能良好、动作可靠的变压器保护具有重要意义。目前，变压器的主保护通常采用差动保护，电流差动保护不需要与保护区外相邻元件的保护在动作值和动作时限上相互配合，在区内故障时可以瞬时动作。但是，变压器空载合闸和区外故障切除电压恢复过程中产生的涌流会导致差动保护误动和延时动作。

为了提高和完善变压器保护的性能，科研工作者的分析和研究主要体现在两方面:一是鉴别励磁涌流的新方法，包括基于模糊信息检索［1］、基于支持向量基［2］、基于人工神经网络［3］、基于模糊神经网络［4］等智能技术的励磁涌流判别方法;二是探索保护新原理，包括基于变压器等值回路方程［5～7］、基 于 时 差 法 原 理［8］、基 于 磁 通 特性［9～12］、基于瞬时功率［10］的保护原理等。这些新方法、新原理在理论研究及应用实现的过程中促进了变压器保护的发展。

现有的基于等值回路方程的变压器保护原理与传统差动保护不同，从解决问题的开始就避开了涌流的影响。但是各个绕组的参数不易获得，如何选取动作方程，如何整定保护判据等问题尚未得到解决。本文在回路方程的基础上，利用一、二次绕组参数与短路参数的关系，推导出单相及三相双绕组、三绕组变压器的动作方程，提出了以正序电流作为制动量的保护判据，并制定了该判据的整定原则。动模试验表明，该判据不受涌流的影响，能够快速、可靠地区分变压器的正常情况和区内故障。

1 原理分析

1.1 单相双绕组变压器

如图1 所示的双绕组单相变压器的“T”型等效电路，正弦稳态下的等值回路方程有:

式中:U1，I1，r1，x1分别为一次绕组的电压、电流、漏电阻、漏电抗;U'2，I'2，r'2，x'2分别为二次绕组归算至一次侧的电压、电流、漏电阻、漏电抗。其中一、二次绕组的漏电抗、漏电阻值是不能求得的参数。由于变压器的短路电阻rk、短路电抗xk和短路阻抗zk是可以求得的参数，而且Im在I1中占的比例很小，可以忽略，因此将一次、二次绕组的参数合并起来有:

图1 单相双绕组变压器“T”型等效电路Fig．1 T-type equivalent circuit of two-winding single-phase transformer

因此，令

定义Δz 为一、二次绕组的不平衡参数。由于漏电阻远远小于漏电感，因此，忽略r1与r'2的差值，近似认为Δz= |jx1－jx'2|。代入式(1)得:

在变压器带负荷运行、区外故障、空载合闸、过激磁、区外故障切除后电压恢复过程的情况下，一、二次绕组的漏电阻及漏电感不会发生变化，则Δz 近似为一常数，即Δz =Δzc(一般变压器的x1与x'2近似相等，Δzc接近于0)。代入式(4)得:

式中:Uunb是指不平衡量，主要是由互感器的传变误差等引起的不平衡分量。

在变压器内部故障的情况下，变压器的内部结构发生变化，一、二次绕组的漏电抗发生变化，Δz不再等于Δzc;则式(5)的等式关系不再满足。因此，定义动作量为ΔU=，对于单相变压器选取一次侧正序电流的基波有效值|I1|作为制动量，对于三相变压器，制动量|I1A|如式(6)所示。这里选用正序电流作制动量，保护判据避免了三相或门制动，更简单方便。

则保护判据为

1.2 单相三绕组变压器

如图2 所示的单相三绕组变压器的“T”型等效电路，列写回路方程有:

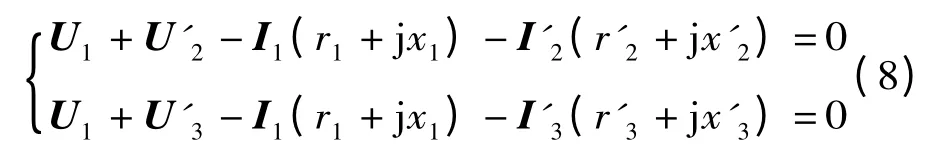
式中:r1，x1是一次侧的等效电阻、等效电抗;r'2，x'2，r'3，x'3是二次、三次绕组归算至一次侧的等效电阻、等效电抗。与双绕组变压器不同，r1，x1，r'2，x'2，r'3，x'3是可以求得的参数，对于三绕组变压器有:

在变压器带负荷运行、区外故障、空载合闸、过激磁、区外故障切除后电压恢复过程的情况下，变压器的结构参数不会发生变化，则ΔU = Uunb，其中Uunb是由互感器传变误差引起的不平衡量。在变压器内部故障时，变压器的结构参数改变，则ΔU ＞Uunb。

图2 单相三绕组变压器“T”型等效电路Fig．2 T-type equivalent circuit of three-winding single-phase transformer

2 动作方程

2.1 三相Y/Y 接法变压器的动作方程

对于如图3 所示的Y/Y 接法的三相变压器，列写回路方程:

可得动作方程为

式中:zka，zkb，zkc分别为A 相、B 相、C 相的短路阻抗。对于三相变压器，短路阻抗zk为已知参数，根据三相绕组对称，认为zka= zkb= zkc= zk。当ΔU1，ΔU2，ΔU3中任一项满足动作判据时，判定为变压器内部故障。

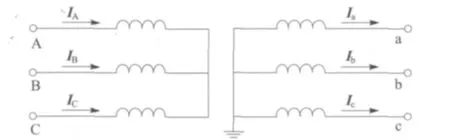
图3 Y/Y 接线的三相变压器Fig．3 Two-winding three-phase transformer with Y/Y connection

2.2 三相Y/△接法变压器的动作方程

如图4 所示的Y/△接法的三相变压器，列写回路方程:

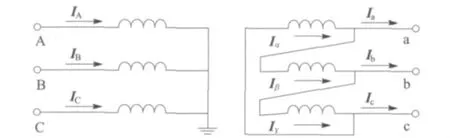
图4 Y/△接法的三相变压器Fig．4 Two-winding three-phase transformer with Y/△connection

根据变压器三相对称，近似认为

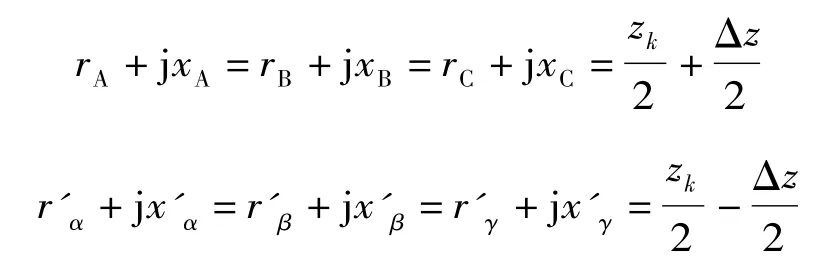
△侧的绕组电流I'α，I'β，I'γ不能直接测量，根据I'a= I'α－ I'β，I'b= I'β－ I'γ，I'c= I'γ－I'α代入上式可得Y/△接法的三相变压器的动作方程为

当ΔU1，ΔU2，ΔU3中任一项满足动作判据时，判定为变压器内部故障。

2.3 三相三绕组变压器的动作方程

如图5 所示，Y/Y/△接线的三相三绕组变压器，列写回路方程有:

式中:UA1，UB1，UC1，IA1，IB1，IC1是 一 次 侧绕组的电压、电流;Ua2，Ub2，Uc2，Ia2，Ib2，Ic2是二次侧绕组归算至一次侧的电压、电流;U'ca3，U'ab3，U'bc3，I'α3，I'β3，I'γ3是 三 次 侧 绕组归算至一次侧的电压、电流;三绕组变压器r1，x1，r'2，x'2，r'3，x'3是可以求得的参数，根据三相绕组对称认为rA+jxA=rB+jxB=rC+jxC=r1+jx1，r'a+jx'a=r'b+jx'b=r'c+jx'c=r'2+jx'2，r'α+ jx'α= r'β+ jx'β= r'γ+ jx'γ= r'3+ jx'3。△侧有I'a3=I'α3－I'β3，I'b3=I'β3－I'γ3，I'c3=I'γ3－I'α3。代入上式整理得到三相三绕组变压器的动作方程如下:

图5 Y/Y/△接线的三相三绕组变压器Fig．5 Three-winding three-phase transformer with Y/Y/△connection

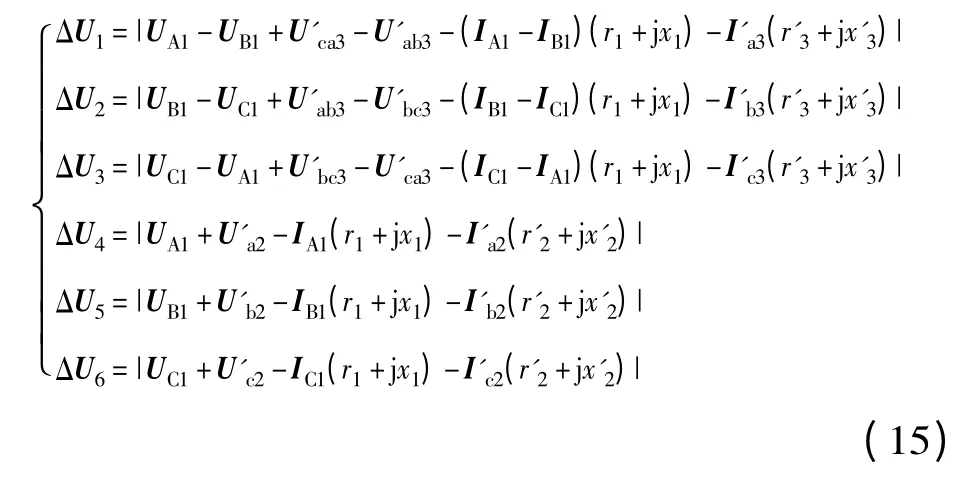
当ΔU1，ΔU2，ΔU3，ΔU4，ΔU5，ΔU6中任一项满足动作判据时，判定为三相三绕组变压器区内故障。

2.4 说明

上文提出的动作方程需要得到变压器二次绕组的端口电压，而目前变压器保护装置获得的是母线电压，不能获得二次绕组端口电压，因此，将该保护用于实际变压器时需要在变压器二次绕组的出线端配置电压互感器以获得端口电压。

3 动模试验及结果分析

3.1 动模试验系统

动模试验变压器采用Y/△-11 接线方式，由三台单相变压器构成，每台变压器结构相同。单相变压器参数为:额定容量为10 kVA，低压侧额定电压为380 V，额定电流为26.3 A，高压侧额定电压为1 kV，额定电流为10 A，空载电流为1.87 %，空载损耗为110 W，短路损耗为200 W，短路电压为14.67 %，高压侧绕组有288 匝，试验中接入78匝，低压侧绕组112 匝全部接入。动模试验系统如图6 所示，试验中系统电压经调压变压器降压为500 V作为试验变压器的电源。rk= r1+ r'2=0.167 Ω，xk=x1+x'2=1.72 Ω。进行试验时，每周波采样100 点，对每种运行状态进行5 次试验。

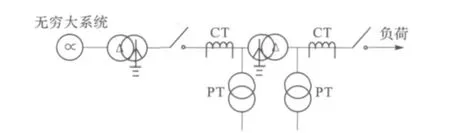
图6 动模试验系统接线图Fig．6 Dynamic power system model

3.2 数据分析

观察空载合闸、区外故障切除后合闸、区内故障情况下动作量的时频特性，结果如图7 所示。动作量在合闸及故障后10 ms左右达到稳定，因此，该保护要在启动元件启动后，经过10 ms的延时，进入保护判据。

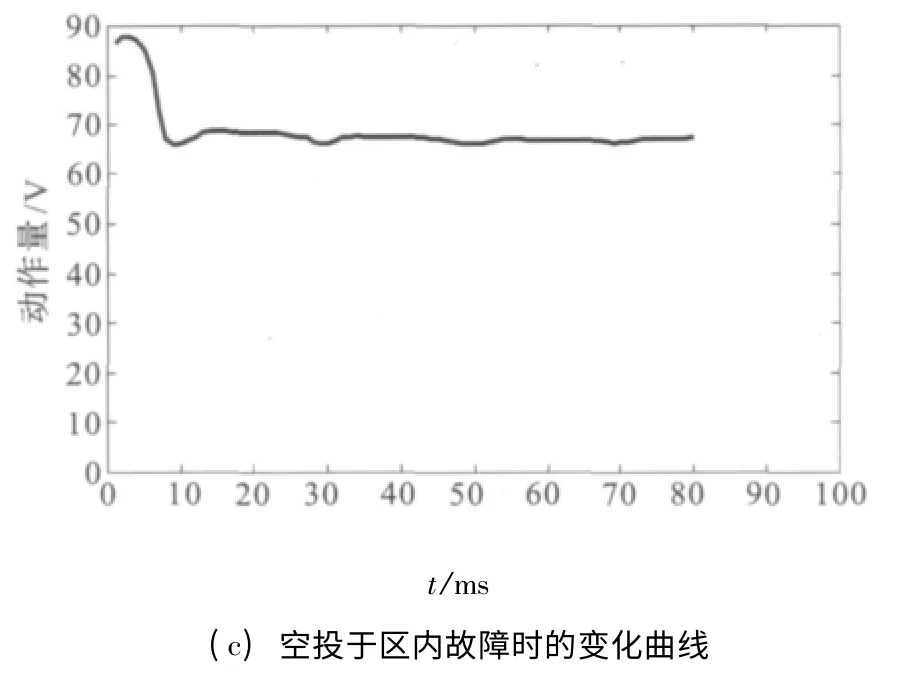
图7 各种状态下动作量的时频特性Fig．7 Time-frequency characteristics of action value in some kinds of states

根据制动量式(6)及动作方程式(13)对试验数据进行分析处理，正常情况包括空载合闸、正常带负荷运行、区外故障切除后合闸，结果如表1 所示。故障情况包括空投于A 相匝间9 %、B相(C 相)匝间18 %、A 相 (B 相)匝地、AB(BC)匝间故障，带负荷A 相匝间9 %、B 相(C相)匝间18 %、A 相(B 相)匝地、AB (BC)匝间故障，故障数据按照故障由轻微到严重的顺序排列，其中ΔUmax为ΔU1，ΔU2，ΔU3中的最大值，结果如表2 所示。

表1 正常情况时的试验结果Tab．1 Test results in normal states

表2 故障情况的试验结果Tab．2 Test results in fault states

3.3 保护判据的整定

(1)由正常情况下的数据可以看出:在变压器正常情况下(包括空载合闸、区外故障切除后合闸、带负荷运行)，动作量ΔUmax很小。

(2)由故障时的数据可以看出:故障由轻微到严重，动作量ΔUmax及制动量|I1A|呈上升趋势。

(3)故障由轻微到严重，动作量ΔUmax的上升趋势逐渐缓慢。

(4)带负荷运行轻微匝间故障，动作量ΔUmax可能接近或小于严重涌流时的ΔUmax。

根据以上规律，总结制动特性的整定原则如下:

(1)最小动作量ΔUset.min，按躲过正常带负荷时的ΔU 整定。

(2)第一拐点|I1A|g.1，整定为带负荷运行时的正序电流。

(3)第二拐点|I1A|g.2，整定为最严重涌流时的正序电流。

(4)K1.set的整定原则，综合考虑最小动作量、第一拐点、第二拐点的整定原则，计算K1=(ΔU－ΔUset.min)/(I1A－ |I1A|g.1)，K'1=K1/Krel，其中，Krel为可靠系数，取1.2 ～1.25。根据K'1的统计结果可得K1的整定范围为1 ～1.5，取K1.set=1.25。

(5)K2.set的整定原则，综合考虑第一斜率、第二拐点的坐标 (|I1A|g.2，ΔUg.2)，计算K2=(ΔU－ΔUg.2)/(I1A－ |I1A|g.2)及K'2=K2/Krel。根据K'2的统计结果可得K2的整定范围为0.8 ～1.0，取K2.set=0.9。

综上，制动特性为

3.4 结果分析

由图8 中的故障数据、正常数据及制动曲线可以看出:故障数据全部在动作区，正常情况的数据全部在制动区。结果表明，该原理能够准确、可靠地区分变压器区内故障和正常情况，而且不受励磁涌流、恢复性涌流的影响。

图8 制动特性曲线Fig．8 Characteristic curve

若空载合闸前变压器已经存在故障，应用本文提出的保护原理能够在合闸后30 ms 快速识别出内部故障，如图7(c)所示。而目前常采用的二次谐波制动差动保护则会受到励磁涌流的影响而闭锁保护，由于励磁涌流衰减很慢，导致保护的动作时间可能会长达数百ms，如图9 所示，若二次谐波制动比为20 %，则在故障后250 ms以后才会开放保护。

图9 空投于故障时二次谐波含量的变化曲线Fig．9 Curve of the second harmonic component in the case of switching onto fault

4 结论

本文基于变压器等值回路方程，利用一、二次绕组参数与短路参数的关系，推导出单相及三相双绕组、三绕组变压器的动作方程;针对双绕组变压器提出了以正序电流作为制动量的保护判据，并制定了该判据的整定原则;对于三绕组变压器，采用单一门槛值的保护判据。结合动模试验系统，对双绕组变压器保护判据进行整定计算，绘制出制动特性曲线，利用空载合闸、区外故障后合闸、正常带负荷等正常情况及空投、正常带负荷运行时发生匝间、相间、匝地等内部故障的仿真结果对保护判据进行了验证。试验结果表明，与二次谐波制动的差动保护判据相比，基于变压器等值回路方程的保护判据具有两个优点: (1)不受励磁涌流的影响，能够快速、准确地识别出区内故障。(2)空投于区内故障时，二次谐波制动的差动保护受涌流的影响会延时动作，而该保护判据能够快速识别故障。

［1］张荣海，熊小伏，夏莹．基于模糊信息检索的变压器差动保护［J］．电力系统保护与控制，2010，38 (16):132-136．Zhang Ronghai，Xiong Xiaofu，Xia Ying．Power transformer differential protection based on fuzzy information retrieval［J］．Power System Protection and Control，2010，38(16):132-136．

［2］王世勇，孙鸣，丁中奎．一种基于支持向量机的变压器励磁涌流判别新方法［J］．继电器，2008，36 (5):1-6．Wang Shiyong，Sun Ming，Ding Zhongkui．A new scheme to distinguish between inrush current and internal fault of transformer based on support vector machine ［J］．Relay，2008，36 (5):1-6．

［3］索娜，李学武．应用BP 神经网络鉴别励磁涌流［J］．电气应用，2008，27 (20):19-22．Suo Na，Li Xuewu．The discrimination of the magnetizing inrush current with BP neural network ［J］．Electro-technical Application，2008，27 (20):19-22．

［4］陈琛，张举，成敬周．基于模糊神经网络的变压器励磁涌流鉴别的研究［J］．华北电力大学学报，2005，32(4):5-8，30．Chen Chen，Zhang Ju，Cheng Jingzhou．Identification of inrush based on fuzzy neural network ［J］．Journal of North China Electric Power University，2005，32 (4):5-8，30．

［5］朱云山，李思．基于等值回路方程的变压器保护装置设计［J］．电力科学与工程，2008，24 (8):29-32．Zhu Yunshan，Li Si．The design of novel transformer protection device based on equivalent circuit equilibrium equation［J］．Electric Power Science and Engineering，2008，24(8):29-32．

［6］郝治国，张保会，褚云龙，等．基于等值回路平衡方程的变压器保护原理［J］．中国电机工程学报，2006，26(10):67-72．Hao Zhiguo，Zhang Baohui，Chu Yunlong，et al．Study on transformer protection principle based on equivalent circuit equilibrium equation ［J］．Proceedings of the CSEE，2006，26 (10):67-72．

［7］黎功华，罗建，杨浩．基于绕组不平衡参数回路方程的变压器保护原理［J］．电力系统自动化，2008，32(6):91-94．Li Gonghua，Luo Jian，Yang Hao．A new transformer protection principle based on winding unbalanced parameter loop equation ［J］．Automation of Electric Power Systems，2008，32 (6):91-94．

［8］徐岩，周霏霏．具有实用性的变压器时差法保护判据的研究［J］．电力系统保护与控制，2011，39 (15):47-51．Xu Yan，Zhou Feifei．A practical transformer protection criterion based on time difference method ［J］．Power System Protection and Control，2011，39 (15):47-51．

［9］谭江平．基于磁通轨迹特征的变压器励磁涌流识别新方法［J］．电力自动化设备，2008，28 (12):77-80．Tan Jiangping．Identification of transformer magnetization inrush current based on magnetic flux track ［J］．Electric Power Automation Equipment，2008，28 (12):77-80．

［10］马静，王增平，吴勋．基于广义瞬时功率的新型变压器保护原理［J］．中国电机工程学报，2008，28(13):78-83．Ma Jing，Wang Zengping，Wu Xun．A novel principle of transformer protection based on generalized instantaneous power ［J］．Proceedings of the CSEE，2008，28 (13):78-83．

［11］孙洋，于超，黄家栋．基于四边形平行度识别变压器励磁涌流的方法［J］．电力科学与工程，2010，26(8):1-3，29．Sun Yang，YU Chao，Huang Jiadong．Method of identify inrush current based on degree of quadrilateral parallelism［J］．Electric Power Science and Engineering，2010，26(8):1-3，29．

［12］王晓翀，李春明．基于小波能量的变压器励磁涌流识别 方 法 ［J］．电 力 科 学 与 工 程，2010，26(8):24-29．Wang Xiaochong，Li Chunming．Method for inrush current detection in transformers based on wavelet transform energies ［J］．Electric Power Science and Engineering，2010，26 (8):24-29．ty，2008，9 (4):51-54．

［4］倪凯．组合预测方法在短期电力负荷预测中的应用研究［D］．广州:中山大学，2009．

［5］蒋晓艳，何川．基于最优组合预测法的电网负荷预测［J］．水电能源科学，2010，28 (3):149-151．Jiang Xiaoyan，He Chuan．Application of optimal combined forecasting method to power grid load forecasting ［J］．Internatinal Journal Hydroeletric Energy，2010，28 (3):149-151．

［6］杨平，董国威．实时灰色预测模型及高效执行算法［J］．自动化技术与应用，2011，30 (7):5-8，21．Yang Ping，Dong Guowei．The real-time grey forecasting model and its implementation algorithm ［J］．Techniques of Automation and Application，2011，30 (7):5-8，21．

［7］吉培荣，胡翔勇，熊冬青．对灰色预测模型的分析与评价［J］．水电能源科学，1999，17 (2):42-44 Ji Peirong，Hu Xiangyong，Xiong Dongqing．Analysis and evaluation to grey forecasting model ［J］．Internatinal Journal Hydroeletric Energy，1999，17 (2):42-44．

［8］范习辉，张勇传．短期电力负荷预测的GM (1，1)模型群方法及应用［J］．水电能源科学，2002，20 (3):77-79．Fan Xihui，Zhang Yongchuan．Power load forecasting using GM (1，1)model cluster ［J］．Internatinal Journal Hydroeletric Energy，2002，20 (3):77-79．