纵向地震激励下倒Y 形主塔斜拉桥的地震易损性分析

焦驰宇， 李建中， 龙佩恒

(1．北京建筑工程学院“工程结构与新材料”北京高等学校工程研究中心，北京 100044;2．同济大学 土木工程防灾国家重点实验室，上海 200092)

0 引言

近年来，大跨度桥梁在滇西北和藏东南以及川西等高烈度地震区的修建日趋增多，因而其地震反映破坏规律不断受到关注［1］。特别是大跨斜拉桥这种典型的非规则桥梁结构，由于其超过了国内外抗震设计规范的应用范围，近年来形成了对单体斜拉桥进行抗震专题研究的科研导向。这种方法无法从宏观上了解一类斜拉桥在高强度地震动下的群体地震损伤特征。地震易损性分析是在地震工程领域了解结构地震损伤特征的一个科学工具。近年来被广泛用于各种桥梁、高层结构的地震易损性分析当中［2］。

总体而言，易损性分析通常可以选用两种方法进行:一是基于现场观测的经验易损性分析方法、二是基于数值模拟的理论易损性分析方法。

经验易损性分析方法［3］主要基于现场观测，对一定区域内不地震水平下的已有震害进行分类统计，最终获得不同地震水平下的结构损伤破坏概率。例如: Basoz、Kiremidjian 基于Northridge 震后的桥梁损伤数据，采用回归分析建立了经验易损性曲线。Shinozuka、Tanaka、Yamazaki、Kriging 等基于神户地震中桥梁的实际地震损伤数据，回归得到了实际地震中的地震易损性曲线。

理论易损性分析方法，通过建立反映某一类桥梁典型结构特征的数值计算模型，选取反映桥址所在场地特征的地震记录，利用非线性动力分析方法求解结构响应，通过前人研究、试验或者专家判断确定不同损伤状态阈值，最后利用概率方法确定结构构件超越某一损伤状态的阈值，最终确定结构的地震易损性曲线。例如:Hwang ＆ Huo［4］针对孟斐斯田纳西州的一座四跨简支梁桥，通过非线性时程分析获得结构的地震响应数据，采用逻辑模型来确定结构在地面运动参数下超越某一损伤状态的条件概率。Karim ＆Yamazaki［5］考虑了四种典型的钢筋混凝土桥墩和两种桥梁结构形式( 隔震与非隔震体系) ，通过非线性时程分析，根据损伤指标和地震动参数，建立起对数正态分布形式的理论易损性曲线。

近年来理论易损性曲线成为求解非规则桥梁结构地震易损性的主要手段，王宇等［6］建立了西部山区典型变墩高公路桥梁非线性分析计算模型，通过纵横向地震易损性分析对各种设计参数对地震易损性的影响进行了比较研究。

对于大跨度斜拉桥这种震害较少、受力复杂的结构形式，理论易损性分析方法是最好的选择。基于此，结合我国现役大跨斜拉桥的结构特点，以III 类场地上近年来大跨度斜拉桥体系中较为流行的倒Y 型主塔斜拉桥为研究对象，选取20 条实测地震波进行增量动力分析，对倒Y 形主塔斜拉桥进行了地震易损性研究。

1 地震易损性分析

1．1 计算模型选取

近年来，国内修建了许多大跨度斜拉桥。通过调查分析现有斜拉桥几何特征，可以得到以下一些典型结构特征:

(1) 双塔、双索面、钢箱梁的漂浮体系是一种常用结构体系。

(2) 主跨主要分布在600 ～800 m 范围。

(3) 大多数大跨斜拉桥一般修建在淤泥质的的河床地基上，受河流冲刷影响，一般采用高桩承台基础。

(4) 为了增加结构的抗扭刚度，通常采用倒Y 型或钻石型桥塔。

选取了一座82 m+262 m+688 m+262 m+82 m 的斜拉桥作为国内大跨斜拉桥的典型桥例:该桥采用倒Y 形主塔，塔高235 m;采用高桩承台基础，冲刷深度为19 m。其桥塔形式如图1 所示。

已有研究表明，漂浮体系斜拉桥在地震过程中拉索、主梁构件基本在弹性阶段，具有很大的安全储备，主塔、辅助墩、过渡墩为主要抗侧力构件。因而，为了更好的考虑斜拉桥主塔、辅助墩、过渡墩的地震损伤破坏特征，利用OpenSees 平台中的纤维梁柱单元对斜拉桥主塔、墩柱进行了模拟，关于模型的材料及几何特性详见文献［7］。此外，为了提高计算效率，采用在中跨施加反对称约束的方法，对半桥模型进行了非线性动力时程分析。模型简图如图2 所示。

图1 倒Y 形斜拉桥主塔立面图(单位:m)

图2 斜拉桥半桥简化模型

1．2 地震动输入

考虑到现有大跨度桥梁一般修建于河道中，其地质条件多为III、IV 类软土。因而从太平洋地震工程研究中心的美国国家地震记录数据库( NGA 数据库) 中选出震中距20 km 以内的III 类场地上20 条实测地震记录进行地震易损性分析，详见表1。地震易损性分析时，将谱加速度Sa( T1 =13．5 s，ξ = 3%) 值按照0．003g 的步长从0．001g 调幅至0．028g，每条地震波设置10 个强度等级，进行增量动力时程分析。

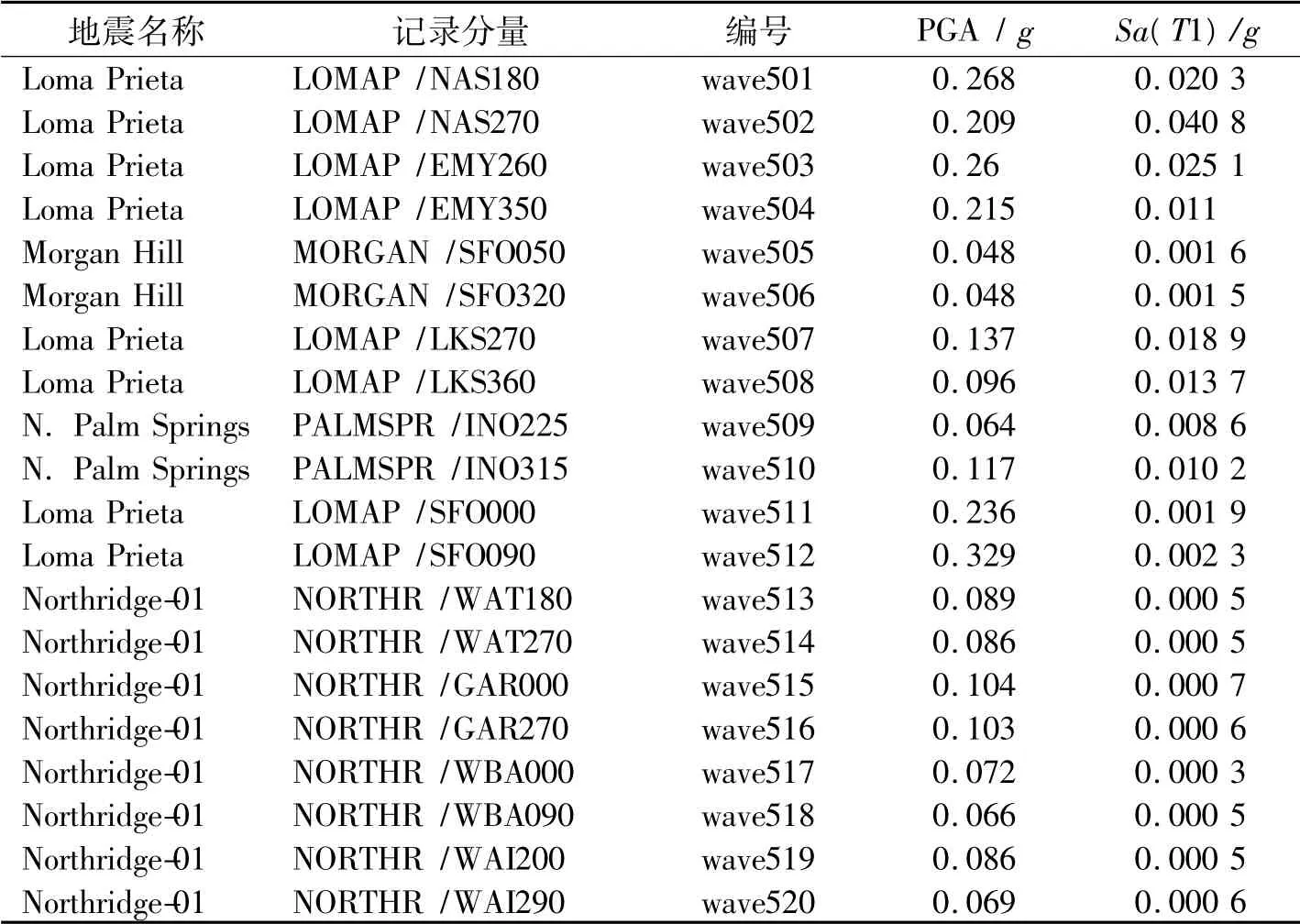
表1 NGA 数据库给出的III 类场地地震波

1．3 损伤状态的定义

众所周知，斜拉桥由许多构件组成，诸如主塔、主梁、拉索、辅助墩、过渡墩、塔柱基础、辅助墩基础、过渡墩基础构成。大跨度斜拉桥易损性分析主要目的有两个，一是确定斜拉桥的最易损伤构件; 二是确定某一构件的最易损伤部位。如前所述，主塔、辅助墩、过渡墩为主要抗侧力构件。大跨斜拉桥的墩柱、主塔属柔性结构，一般以弯曲变形为主，因而可采用恒载轴力作用下关键截面的曲率作为截面的损伤指标。以文献［8］中提出的针对Tecoma 悬索桥塔柱结构的材料应变状态的定义为基础，参考同类文献的应变损伤状态的确定方法，定义了基于材料应变状态的截面损伤指标如下( εs为最外侧钢筋应变，εcc、εc分别为最外侧约束、非约束混凝土应变) :

(1) 无损伤。混凝土没有开裂，钢筋没有屈服。应变损伤指标εs≤εy= 0．001 675。

(2) 轻微损伤。混凝土构件开始开裂但并裂缝小于1 cm，钢筋进入屈服阶段但并没有进入强化阶段。应变损伤指标0．001 675 ＜εs≤εh= 0．015;εc≤2εco= 0．004。

(3) 中等损伤。截面损伤在经济上、技术上可以修复。应变损伤指标0．015 ＜εs≤0．55εsu= 0．049 5;0．004 ＜εcc≤0．75εccu= 0．007 875。

(4) 严重损伤。截面不能修复，承载力开始下降。应变损伤指标0．55 ＜εs≤εsu= 0．09;0．75εccu＜εcc≤εccu= 0．010 5。

(5) 完全损伤。构件变形达到极限状态，结构倒塌。应变损伤指标εs＞εsu= 0．09;εcc＞εccu=0．010 5。根据该指标可求出相应损伤状态的曲率阈值。图3 为沿塔柱截面的不同损伤状态界限值。

1．4 易损性曲线求解方法

目前，理论易损性曲线的生成方法主要有三种:一是超越损伤状态的频数统计法;二是直接回归概率需求模型线性拟合法;三是能力需求比模型的曲线拟合法。比较研究表明: 频数统计法求得的结果依赖于非线性时程分析次数，要提高精度必须加大非线性时程分析的次数;选用逻辑变量统计超越或不超越某一损伤状态的概率，容易导致较大的系统误差;而采用二次多项式回归，一方面能减小回归的离散性，另一方面直接应用能力需求比的拟合标准差，更具客观性、可靠性。

因此，采用能力需求比模型的曲线拟合法生成主塔、墩柱的地震易损性曲线。在此简单介绍易损性曲线的求解方法:

步骤1:计算不同地震动强度下的截面曲率需求，计算不同损伤状态下的截面曲率能力。

步骤2:取强度指标的自然对数( ln( Sa) 作为自变量;( Sa 为结构基本周期对应谱加速度值) 以需求与能力比值的对数( ln( Sd/Sc4) ) 作为因变量，利用最小二乘数拟合曲线法进行非线性回归。回归后( ln( Sd/Sc4) ) 可以表示成( ln( Sa) ) 的函数。

式中，Sr为样本点的残差平方和，n 为样本点数。

步骤3:由于ln( Sd/Sc4) 服从正态分布，针对不同的Sa 代入拟合公式(1) 可得到不同的μ 和σ 值。求解超越概率Pf的公式(3) ( 其实质是累积正态分布函数值) ，可以求出不同强度地震动水平下主塔塔底截面完全损伤的超越概率值。

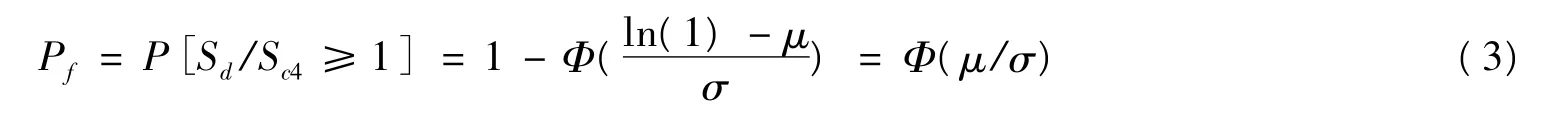
以塔底截面完全损伤状态的易损性曲线求解过程为例，图4 为以增量动力分析结果进行回归分析，图5 为获得结构易损性曲线的结果。

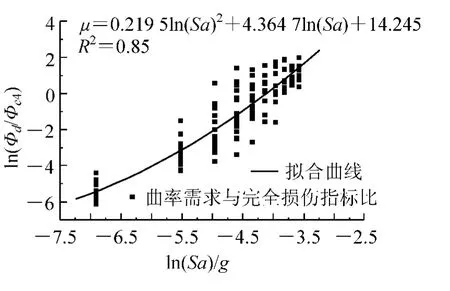
图4 塔底截面的曲率需求与完全损伤指标比

1．5 易损性分析主要结果

依据上述方法可以求出主塔塔柱单元各截面的易损性曲线，将塔柱各截面的易损性曲线沿塔高画在三维图中( 如图6 所示) ，可以看出主塔沿塔高的易损部位。

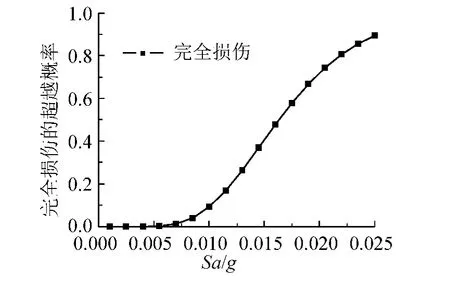
图5 主塔下塔底截面完全损伤的易损性曲线

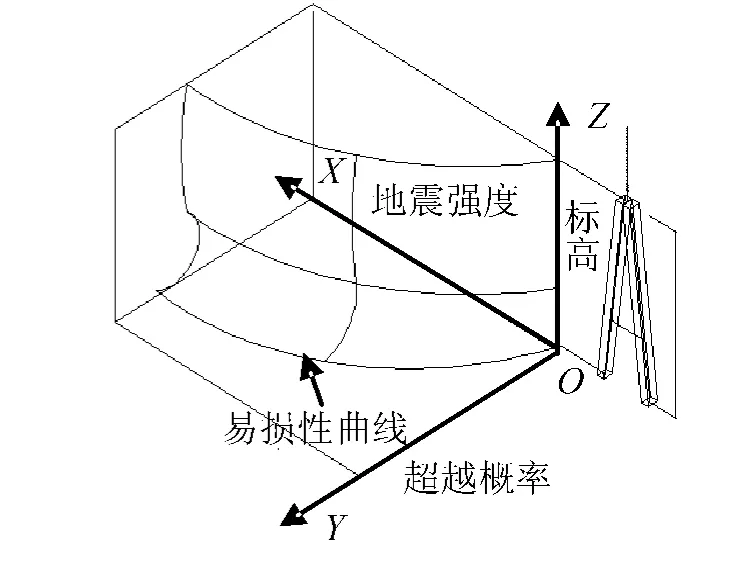
图6 主塔损伤概率三维图坐标系统

由图7 可以看出，用Sa( T1) 作为结构地震强度指标时，主塔轻微损伤的超越概率较高。在Sa( T1) =0．004g 时，主塔下塔底轻微损伤的超越概率达到50% 左右，在0．009g 时主塔下塔底中等损伤的超越概率达到50% 左右，在0．012g 时主塔下塔底严重损伤的超越概率达到50% 左右，在0．017 8g 时主塔下塔底完全损伤的超越概率达到50% 左右。在Sa( T1) = 0．006g 时，主塔中塔底轻微损伤的超越概率达到50% 左右，在Sa( T1) = 0．019g 时，主塔中塔底中等损伤的超越概率达到50%，在Sa( T1) = 0．028g 时，主塔中塔底严重损伤的超越概率达到50%;在Sa( T1) = 0．028g 时，主塔中塔底完全损伤的超越概率达到25%左右。

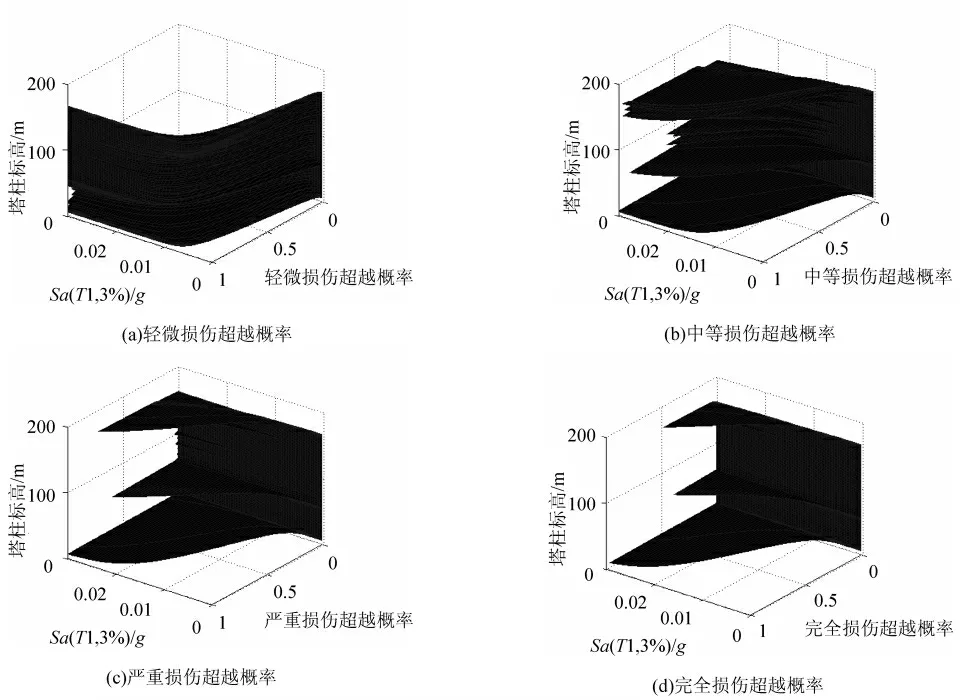
图7 纵桥向激励下斜拉桥主塔沿塔高损伤超越概率分布

四种损伤状态下，随着地震动强度的增加，主塔各截面损伤概率均逐步增高。在同一地震强度水平下各种损伤的超越概率中，主塔下塔底、中塔底、中塔顶三个截面的超越概率在主塔各截面中是较高的，而其中又以主塔下塔底截面为最高。

因而可以认为III 类场地土条件下:下塔底，中塔底和中塔顶是主塔结构的易损部位，其中下塔底是最易损的。

与此类似，可以得到辅助墩、过渡墩的沿墩高的地震损伤超越概率。因篇幅有限，在此给出辅助墩、过渡墩沿墩高的完全损伤状态的超越概率。如图8、图9 所示。

随着地震动强度的增加，过渡墩各截面损伤概率均逐步增高。在同一地震强度水平下各种损伤的超越概率中，墩底实心段底截面和墩底渐变段底截面的超越概率在过渡墩各截面中是最高的。因而可以认为III 类场地土纵桥向地震输入下:过渡墩墩底实心段和墩底渐变段是易损部位。为了比较各构件同一损伤状态超越概率的大小，将同一地震强度水平下，某构件所有截面同一损伤状态的最大超越概率作为该构件该种损伤状态的超越概率。在此基础上，将各构件同一损伤状态的超越概率画在同一张图上，可以分析出不同构件在不同强度水平下损伤超越概率的相对大小，进而可以得出构件易损性的相对大小，见图10。

在III 类场地纵桥向地震输入下，斜拉桥各构件按轻微损伤或中等损伤超越概率由高到低依次为:过渡墩桩基＞主塔桩基＞辅助墩桩基＞过渡墩＞辅助墩＞主塔;按严重损伤和完全损伤的超越概率由高到低依次为:在较低的地震强度水平下，主塔桩基＞过渡墩桩基＞辅助墩桩基＞过渡墩＞辅助墩＞主塔。在较高的地震强度水平下，主塔桩基=过渡墩桩基=辅助墩桩基＞主塔＞过渡墩＞辅助墩。

在III 类场地纵桥向地震输入下，斜拉桥各构件四种损伤超越概率中，主塔桩基、辅助墩桩基、过渡墩桩基的超越概率最接近，而过渡墩、辅助墩、主塔的超越概率差别较明显，可以认为前三种构件之间的易损性差别不大，而后三种构件的易损性差别较大。通过对各构件易损性的比较，可以看出: 在III 类场地纵桥向地震输入下，斜拉桥的主塔是最不易损的构件，而桩基是最易损的构件。

图8 辅助墩完全损伤沿墩高概率分布

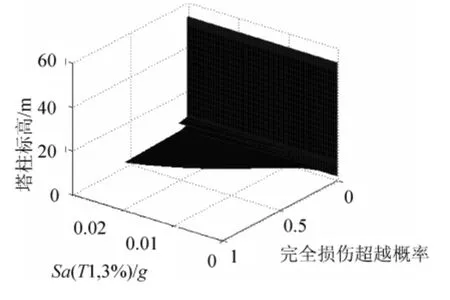
图9 过渡墩完全损伤沿墩高概率分布

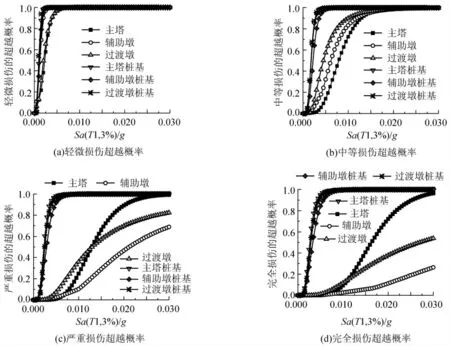
图10 斜拉桥各构件易损性之间的比较

2 结论

通过对倒Y 型主塔斜拉桥纵桥向的地震易损性分析，可以得出以下结论:

(1) 地震易损性分析是确定大跨斜拉桥易损构件、构件易损部位的有效工具。

(2) 在纵向地震激励下，我国倒Y 形主塔大跨度斜拉桥的最易损伤构件是桩基础，特别是主塔桩基础。在设计中应加强其抗震能力，以保证结构的抗震性能。

(3) 对某一关键构件，画出沿构件长度方向的地震易损性曲线，可以获得该构件最易损伤部位。

(4) 在纵向地震激励下，倒Y 形主塔的易损部位集中在三个区域:中塔柱底部，中塔柱顶部，下塔柱底部。

［1］段昕智，徐艳，李建中． 近断层地震脉冲效应对大跨度桥梁地震响应的影响［J］． 石家庄铁道大学学报:自然科学版，2011，24(3) :1-6．

［2］Pan Y，Agrawal A K，Ghosn M． Seismic fragillity of continuous steel highway bridges in New York State［J］． Journal of Bridge Engineering，2007，12(6) :689-699．

［3］张菊辉．基于数值模拟的规则梁桥墩柱的地震易损性分析［D］． 上海: 同济大学土木工程学院，2006．

［4］Hwang，Huo H H M ，J R． Probabilistic seismic damage assessment of highway bridges［C］//The 6th U．S． National Conference on Earthquake Engineering．Washington:Seattle，1998．

［5］Karim K R，Yamazaki F． A simplified method of constructing fragility curves for highway bridges［J］． Earthquake Engineering and Structural Dynamics，2003，32:1603-1626．

［6］王宇．变墩高公路桥梁的地震易损性分析［D］． 上海: 同济大学土木工程学院，2007．

［7］Jiao chiyu，Li jianzhong，Fan lichu． Nonlinear seismic response analysis and seismic performance evaluation of A RC cablestayed bridge tower using IDA method［C］//the 14th World Conference on Earthquake Engineering．Beijing:［s．n．］，2008:12-17．

［8］Arzoumanidis S，Shama AA，Marlow SJ，Orsolini GO． The New Tacoma Narrows Suspension Bridge: Critical Issues in Seismic Analysis and Design［C］//Structures 2005． New York: ［s．n．］，2005:21-21．