超声测距技术与非接触静电测量一体化设计方法研究

董振旗，刘 鹏，周永涛，杨 庆

（第二炮兵工程大学 陕西 西安 710025）

静电现象指相对于观察者而言，所带的电荷处于静止或缓慢变化的相对稳定状态[1]。静电产生的原因很多，如固体起电、粉体的静电起电、液体起电、气体的静电起电、人体的静电起电等[2]。静电对人们的日常生产和生活的影响越来越大。静电的应用和危害也日益引起世界的关注，一是静电技术已被广泛地应用到各行各业，如电子照相、静电存储、静电复印机等；二是静电造成的危害甚至灾难也时有发生。如静电的放电引起爆炸、干扰通信等[3]。为了防止或避免静电带来了的危害，必定要采取一系列防护措施，而静电监测、快速测量是进行有效防护的基础。因此，研究利用超声测距技术与非接触式静电测量一体化静电测量方式与设计方法，对于静电快速测量有着重要作用。

1 静电测试中问题分析

在高绝缘介质中的电荷不能自由移动，各不同部位的电位不同，只能用静电感应或空气电离的原理进行测试。而前者是将最探极靠近带电体，测量其表面电位，实质上是对其表面的电场的测量。非接触式静电测量仪器大致分为感应式和电阻分压式；感应式仪表中多采用直接放大式、旋叶式和振动电容式等[4]。利用非接触式静电测量仪表对静电测量的基本原理如图1所示。是将探头置于带电体附近，不与被测带电体相接触；通过对带电体表面电场的测量获得其表面电位的数值。在实际对静电测量中，其测量方法中仪表与被测量物体（如静电板）的距离有着重要关系。

图1 非接触式静电测量仪表测量原理Fig.1 Measurement principle of the non-contact inductive electrostatic measuring instruments

以EST101型防爆静电电压表为例，它是一种非接触直感式静电电压表，结构原理如图2所示；当该电压表离带静电电压的静电板不同距离时，电压表则显示出不同数值；距离越近则显示数值越大，否则相反。要真正测量出被测量物体的静电电压值，必须测量出距离值，然后按照给出的“乘数k与测量距离d的关系曲线”对应关系数值进行换算[5]，如图3所示，才能得到被测量物体具有的静电电压值。当d=10 cm，对应的k=1.0；如果电压表显示数值Z=1.85 kV，则被测量物体（如静电板）具有的静电电压值U（t）按公式（1）计算为：

从测量过程中分析可知，由于该电压表无测量距离的功能，以目测方法测出d，因目测不准确，导致U（t）误差较大。要精确测量出U（t），就必须准确测量出d，查找出k值，通过计算才能真正测量出U（t）值，这样一种测量方式在实际测量中就显得比较繁琐，导致测量不准。其他静电感应式非接触式静电电压表的使用中，也存在内似问题。

图2 EST101型防爆静电电压表结构原理Fig.2 Structural principle of EST101 explosion-proof electrostatic voltmeter

图3 EST101型静电电压表乘数k与测量距离d的关系曲线Fig.3 The curve between the multiplier k and the distance d on the EST101 explosion-proof electrostatic voltmeter

针对上述存在问题，根据感应式非接触式静电电压表结构和工作原理，分析可知，引起上述问题根本原因在于采用的是电容式感应探头。以电容式感应探头组成的EST101型防爆静电电压表，它的输入电路形式如图4所示。A为被测静电体，T为电容直感测量探头，C0表示在A和T之间的电容，C1为探头的对地电容，R和C分别为仪表的输入电阻和电容。设A对地的实际静电电压为U0，所测得电压U（t）符合式（2）。

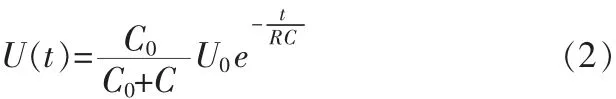
由式（2）可知，当T与A间的距离发生变化时，则C0发生变化，从而导致U（t）发生变化，使仪表测量显示数值发生变化。对于其他形式的电容感应式非接触式静电电压表，同样是因为与测量距离变化，而使仪表测量显示数值发生变化。

图4 EST101型静电电压表工作原理图Fig.4 Working schematic of the EST101 explosion-proof electrostatic voltmeter

2 一体化新型静电测量装置的设计

为解决感应式非接触式静电电压表，在实际测量中比较繁琐和测量换算的问题，文中提出利用超声测距技术与非接触静电测量技术一体化的测量方式，来解决上述问题。

2.1 超声测距技术应用分析

感应式非接触式静电电压表，在规定测量距离内实施静电测量的同时，附加一种超声测距系统电路，能够直接显示出与带静电体的测量距离，就可减少原来测量过程中的繁琐；如果静电测量与超声距离测量组合成一体，即组成新型静电测量装置；超声测距系统电路获得的数据信息与静电测量电路测量的数据信息，经过数据处理电路，按照静电电压表乘数k与测量距离d的关系进行换算，就能使新型静电测量装置直接显示出被测带静电体的实际静电电压值，就能达到快速静电测量的目的。

2.2 新型静电测量装置一体化原理设计

一体化设计，实际上是在原静电电压表原理基础上附加一种超声测距电路和数据处理电路、数字显示电路，并形成一个整机测量状态，整机结构原理如图5所示。A为被静电体，T1为电容直感测量探头，T2为超声探头，C0表示A与探头间的电容，d为T1、T2与被测静电体的距离。当一体化新型静电测量装置两探头与A间的距离发生变化时，如距离减小，则C0电容量增大，T1使静电测量电路输出的信号幅度增大；同时，T2使超声测距电路输出信号也发生变化；两路信号同时输出到数据处理电路；数据处理电路把两路电信号首先进行模/数转换，然后进行数据处理，并按照原静电电压表乘数k与测量距离d的关系进行换算，输出到显示电路；使显示器电路显示出A所带静电电压值。在结构方面，T1和静电测量电路与T2和测距电路是两个原理不同的独立电路形式，数据处理电路它包括模/数转换器、存储器、运算器等，数字显示电路则包括译码器、驱动器和LCD模块等。

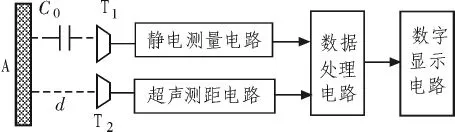
图5 一体化新型静电测量装置原理图Fig.5 Schematic of the new non-contact static electricity measurement equipment

2.3 新型静电测量装置对超声距离电路性能参数的要求

超声距离电路在一体化新型静电测量装置设计中至关重要，其准确性、稳定性事关装置的测量精度。超声波发射器定期发送超声波，遇到被测物体时发生反射，反射波经超声波接收器接收并转化为电信号，只要测出发送和接收的时间差，即可测出超声测距电路到被测物体之间的距离[6]。

超声波在空气传播过程中，由于空气吸收衰减和扩散损失，声强随着传播距离的增大而衰减，而超声波的衰减随频率增大而成指数增加[7]。从图3中分析出，常用的测量距离为10 cm，最小测量距离dmin为1.0 cm，最大测量距离dmax为20.0 cm。在室温下，空气中的声速c为345 m/s，考虑反射式测量有2倍路程，则被测距离与测距时间关系为式（3）：

可计算出，dmin=1.0 cm 时，tmin=58 μs；dmax=20.0 cm 时，tmax=1 160 μs。

由于选用气相、窄波束、40 kHz的超声波传感器，按式（4）计算：

可见：dmin近似为λ，这样会使超声测距电路发射与接收的功能难以实现。有效反射目标应大于至少10个波长以上，对于非垂直于发射波束的目标，大波束角的传感器通常可以获得更强的回波信号，而波束角越窄对于减小散射波的干扰越有利[8]。

由此，选择12个波长，有效反射目标距离约为10 cm，能够有效保证发射与接收功能的可靠性。这样的设计符合图3中的常用测量距离和dmax的要求，但不符合dmin的要求，这一问题将在一体化整机设计中解决。结合静电测量实际，依据图3中给出的测量距离范围1.0～20.0 cm，使其测量范围处在最佳的测量精度范围内，便于测距的调整和小型化设计，选择超声测距电路最大测量距离为150 cm。

静电测量对精度要求越来越高，从图3中看出测量距离误差越小，带来的静电测量精度就越高。误差虽不可能消除，但可以追求更小；根据技术条件，设计超声测距电路的测量误差≤0.1%。目前，超声波测距误差通过采取温度补偿、湿度控制等措施，在150 cm范围内测量误差不超过1 mm[9]。

2.4 新型静电测量装置一体化结构设计

根据图5一体化原理设计，设计整机结构如图6所示。主要由3部分组成，即静电测量电路、超声波测距电路、数据处理与显示电路组成。静电测量电路其设计技术与EST101型防爆静电电压表的功能、性能基本相符，其距离变化范围在 1～20 cm 间变化[10]。

按照设计的超声波测距电路的测距性能，利用相对测距方法，设计确定最小测量距离d1为20 cm，测量距离d2为40cm，并对应于EST101型防爆静电电压表的测量范围1～20 cm；这种相对测距方法即解决了超声波测量较短距离性能不足问题，又能在数据处理与显示电路中利用程序设计可以实现。

图6 一体化新型静电测量装置结构图Fig.6 Chart of the new non-contact static electricity measurement equipment

数据处理与显示电路，采用功耗低、速度快，具有一定数据储存功能单片机芯片设计而成，能够将静电测量电路、超声波测距电路的模拟信号进行模/数转换，并能进行换算。依据图3给出的乘数k与测量距离d的关系数据点，进行曲线拟合，并建立乘数k、测量距离d与测试静电电压值换算模型；依据模型和操作功能要求，设计程序。显示电路，主要由3位半液晶数字显示器组成，直接显示被测静电体电压值。

3 可行性试验分析

运用EST101型防爆静电电压表和MS6450超声波测距仪，按照图6的结构进行设计原理与方法的可行性验证。由于MS6450最小测距为60 cm，最大测距为1 500 cm，运用相对测距测量方法，选择60 cm至80 cm对应于EST101型防爆静电电压表的测量范围1 cm至20 cm，测量数据如表1所示。按EST101型防爆静电电压表使用说明书给出的乘数k与测量距离d的关系曲线，依据图3建立的乘数k与测量距离d的换算模型为式（5）：

按照换算模型与测量功能的要求，设计程序；结合EST101型防爆静电电压表和MS6450超声波测距仪测量数据，运用MC—51单片机开发系统进行程序运行与数据换算，得出所测量的被测量静电物体的静电电压值如表1所示。

表1 一体化新型静电测量装置相对距离测量模拟实验数据Tab.1 Relative distance simulation data measured by the new non-contact static electricity measurement equipment

表1是在实验室温度为20℃、相对湿度为45%RH的环境下测试的。可以看出，MS6450超声波测距仪在60～80 cm范围内，显示的数值与实际距离的最大误差为+0.2 cm，实际距离与EST101型防爆静电电压表静电测量时的距离误差只有±0.1 cm。EST101型防爆静电电压表静电测量换算电压与开发系统显示值的最大误差为1.4%，与被测静电体静电电压的最大误差为3.2%。这样测算数据基本符合静电测量的要求，可以说明采用超声波测距与非接触静电测量一体化静电测量方式与一体化新型静电测量装置的结构设计思想是可行的。

4 结束语

非接触静电测量，测量读数与测量距离有着重要关系。运用超声波测距技术与非接触静电测量技术组成一体化新的静电测量方式；采用相对测距方法，设计出精度、稳定性较高的测距电路，能够随时的检测静电测量距离，并与静电测量电路形成一体化新型静电测量装置设计方法；静电测量电路、超声测距电路和数据处理与显示电路等组成的新型静电测量装置结构，通过试验验证具有很高的可行性，能够较好解决非接触静电测量繁琐、手持仪表晃动带来的测量误差问题。

[1]张宝铭，林文荻.静电防护技术手册[M].北京:电子工业出版社，2000.

[2]刘尚合，武占成.静电放电及危害防护[M].北京:北京邮电大学出版社，2004.

[3]毛六平，唐艳.静电测量及其程序设计[J].仪器与仪表，2001，18（1）:21－22.MAO Liu-ping，TANG Yan.Electrostatic measurement and programdesign[J].Instrument and Control，2001，18（1）:21－22.

[4]张荣奇，谭志良.常用静电测量技术及其特点[J].装备环境工程，2007，10（5）:85－86.ZHANG Rong-qi，TAN Zhi-liang.The technology and feature of common electrostatic measurement[J].Equipment Environmental Engineering，2007，10（5）:85－86.

[5]薛海峰，等.EST101型静电电压表（使用说明书）[EB/OL].北京亿艾迪科技有限公司.http://www.ESD－china.com

[6]王峰，葛立峰.一种高精度超声测距系统的设计[J].计算机技术与发展，2008，6（1）:229－230.WANG Feng，GE Li-feng.The design of high-precision ultrasonic distance measurement system[J].Computer Technology and Development，2008，6（1）:229－230.

[7]何希才，薛永毅.传感器技术及应用[M].北京：北京航空航天大学出版社，2005.

[8]Herrington D R.Ultrasonic range finder uses few components[J].EDN，1999（6）:23－26.

[9]苏炜，龚壁建.超声波测距误差分析 [J].传感器技术，2004，8（6）:9－11.SU Wei，GONG Bi-jian.Error analysis of the ultrasonic distance measurement[J].Journal of Transducer Technology，2004， 8（1）:9－11.

[10]王永伟，秦小安，曾祥君，等.不受行波波速影响的输电线路故障定位新方法[J].陕西电力，2011（7）：1－4.WANG Yong-wei，QIN Xian-an，ZENG Xiang-jun，et al.New method of high voltage transmission line traveling wave fault location avoiding traveling wave influence[J].Shaanxi Electric Power，2011（7）：1－4.