卷积完全匹配层在二维声波吸收流体介质中的有限元计算

李义丰，汪胜祥

(1.南京工业大学 电子与信息工程学院，南京 210009;2.法国电子、微电子及纳米技术研究所，里尔 59652)

基于计算机有限存储空间和节约计算时间的考虑，在模拟计算声波在无限或半无限介质中的传播时要解决由计算边界的截断而引起的边界反射问题。因此，必须要有合适的边界条件来减小或消除由于边界截断而引起的反射。完全匹配层Perfectly Matched Layer(PML)是由Berenger［1］于1994年提出的一种应用于电磁波截断计算的边界吸收条件。其是一种鲁棒且有效的吸收边界条件［2］，理论证实在进行数值离散前，该PML层对任何频率及任何方向上的入射波在截断面上均不发生反射［1，3］。其作为经典技术被广泛地应用于声波［4］及弹性波［3，5］的数值计算中。但其缺点是要对计算场进行分裂，中间变量较多，场方程较为繁琐，对倾斜入射波及表面波吸收效果较差。

现在，由Roden和 Gedney［6］所提出的基于复坐标变换并利用复频移扩展坐标形式吸收参数的卷积完全匹配层Convolution Perfectly Matched Layer(CPML)在数值计算中得到了广泛的应用，其被有效地应用于不均匀介质、有耗介质、色散介质、各向异性介质及非线性介质的截断计算中［7-9］。与经典PML相比，CPML的主要优势在于其不需要把场分裂开，形式简单，易于实现;其对倾斜入射波和表面波有着比PML更好的吸收效果［10-12］;并有效地解决了渐消波边界反射问题以及长时间计算［13］而引起的边界反射问题。

本文将CPML吸收边界层应用于二维吸收声波的截断计算中，分别在时域及频域中推导出引入CPML边界条件的吸收流体的波动方程，并在有限元(FEM)计算软件COMSOL中完成其时域的计算。计算过程中，通过在COMSOL中选择与所推导出来的方程相对应的计算模型，并设置相应的系数参数来完成运算。相对于CPML的时域有限差分 (FDTD)计算而言，在COMSOL中的有限元 (FEM)计算过程变得更加简单和易于实现。

1 吸收流体二维CPML声波方程的推导

在直角坐标系中，基于牛顿运动定律，二维吸收流体媒质的时域声波方程如下:

式中v、w分别为x、y方向上的粒子速度，p代表的是声压，ρ0、c0及r分别为媒质的密度、声速及吸收系数。吸收系数r用来描述物理介质的吸收损失特性。通常对于吸收介质而言，速度c及系数r是频率依赖的。然而，在一定的频率范围内，我们可以认为c及r是可以频率独立的，在很多实验测量中这一点已经被证实［14］。因此，为了简便起见，在本文的研究中介质假定为是非频散的，即系数c及r在所感兴趣的频带范围内是频率独立的。

1.1 CPML频域声波方程

为了将CPML卷积完全匹配层引入到方程中，首先，将上述方程式(1)～(3)进行傅里叶变换，得到频域中的声波方程。其次，在频域中采用如下的复坐标变换［15］:

式中，sx和sy是复频移 (Complex Frequency Shifthed)扩展坐标变量，其表达式由Kuzuoglu和 Mittra［16］以如下形式给出:

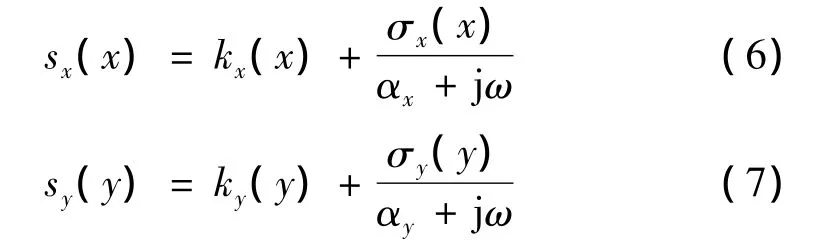
其中，kx，y≥1，σx，y≥0 和 αx，y≥0。在 CPML 匹配层中，实数部分kx，y是为了衰减渐消波而引入的尺度因子，虚数部分 σx，y是该匹配层衰减透射波的衰减参数，αx，y是吸收层中完成Butterworth滤波的一个频率依赖项［2］。在非 CPML 吸收层中，kx，y=1 且 σx，y=0。扩展坐标变量的使用使得CPML层具有比PML层更优越的性能:它能更有效吸收表面波［12］，并有效解决由于大尺寸计算［11］及长时间计算［13］所引起的计算不稳定问题。这样方程式(1)～(3)将变为如下形式的方程组:

式中为变量u的傅里叶变换。为了在有限元软件COMSOL中实现对上述方程组的求解计算，方程式(8)～(10)需要被改写成通用形式的稳态偏微分(PDE)方程，最终得到了频域形式的CPML方程为:

其中，

在sx和sy中，kx、σx及 αx的表达式将在数值仿真部分给出，ky、σy及 αy分别具有与kx、σx和 αx一样的表达式，仅仅需要将x替换为y。

1.2 CPML时域声波方程

为了得到时域中吸收声波的CPML方程，需将频域中CPML的方程式 (8)～(10)进行傅里叶逆变换，并利用傅里叶变换的卷积定理，首先得到时域中卷积形式的声波方程。卷积过程的消除过程可以参见文献［17］，最终得到的消除了卷积且带有记忆变量［18-19］时间偏导的系统时域方程如下:

式中，δx= σx，/kx，βx= σx，/kx+ αx，δy和 βy分别是与 δx和βx类似的表达式，仅需用y替换x;A，B，C和D是为了消除卷积而引入的记忆变量，在非CPML吸收层，他们的值为零，所以他们的一阶导数仅仅在整个计算区域的一小部分被求解。为了在COMSOL软件中实现对上述方程组的求解，将方程式 (15)对时间再次求偏导后，把式(13)和式 (14)带入其中便得到如下的两阶方程:

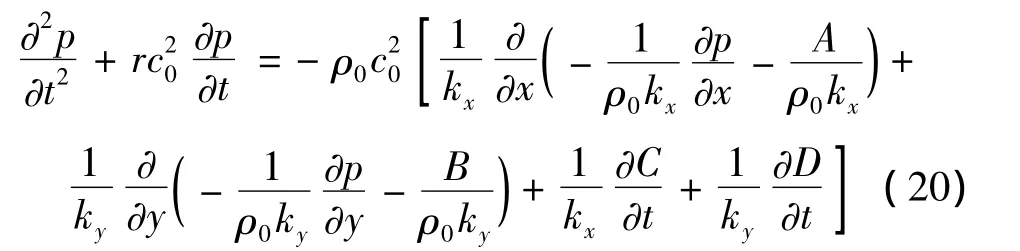
最后得到如下的在方程右边仅含源项的系统方程:

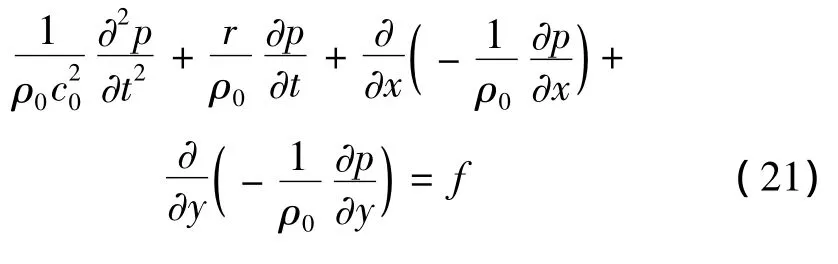
其中:

式(22)中，k'x，y=kx，y-1，C'= ∂C/∂t，D'= ∂D/∂t。变量C'及D'对时间的偏导由如下两个方程分别给出:

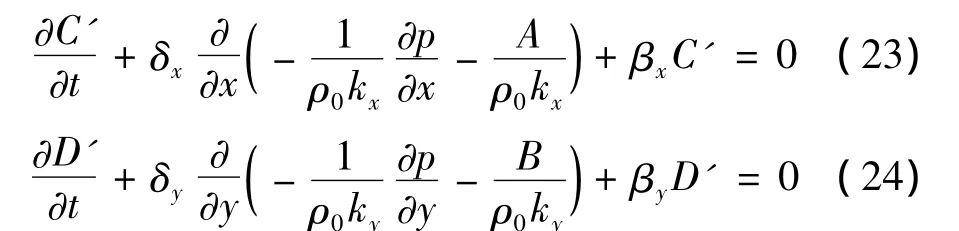
由式(21)可以看出，有关CPML的参数项只是作为源项f出现在最初的初始方程的右边。相对于经典PML层而言，CPML层中为了消除卷积而引入的记忆变量的数量(4个)要少于PML层中由于需要把场分裂开而引入的变量的数量(6个)，因而CPML层所需的总体存储空间会变的更少。

2 数值仿真计算

在此部分，我们测试CPML匹配层对二维声波在吸收流体介质中的吸收性能，为此建立了如图1所示的数值计算模型，19.2 mm×19.2 mm二维计算空间被划分为64×64个FEM计算网格，在四周有8个计算网格厚度的CPML吸收层。信号源S位于数值计算空间的中心，选取A及B两点作为声波压力场p的测试点。如图所示，A点与B点距离左边CPML层均为0.3 mm，A点位于与信号源S同一高度的水平线上，B点距离上边的CPML层为0.3 mm。

图1 CPML二维数值计算模型Fig.1 2D CPML numerical calculation model

数值计算所应用的介质参数为:声速为c0=1 500 m/s，密度为 ρ0=1 000 kg/m3，吸收系数为r=2 ×10-5s/m2，最大的计算频率为fmax=106Hz。所使用的信号源S是Gaussian函数的一阶时间导数信号源，其具有1.5 mm的直径，表达式为:

式中:tw=1.0 ×10-6s，信号源滞后时间t0=5.0 ×10-6s。在扩展坐标变量sx中，所应用的x方向的CPML参数的表达式如下:

运算时，kmax=0，αmax=2π ×105，n1=3，n2=0，n3=1和:

式中，x0和d分别为CPML层的起始位置坐标和厚度;R0=2×10-5是理论上的反射系数。

首先，实现频域的运算，即在COMSOL软件中利用其通用形式的PDE频域计算模型式(30)对式(11)和式(12)进行有限元求解。

计算时，

上式(32)中，右边第一项为式(12)，f'为所用信号源函数式(25)在频域中的表达式。计算时频率步长为Δf=20 kHz，频率变化范围为fmin=20 kHz，fmax=1 MHz。图2为频域中的计算结果，分别为波形在频率为f=40 kHz，380 kHz，740 kHz和 960 kHz 时的波形快照图。从中我们可以定性看出CPML匹配层对各个频率的声波起到了很好的吸收效果，在截断边界处没有反射发生。

其次，进行时域的求解，在COMSOL软件中对时域CPML方程式(21)和式(22)进行有限元求解。为了节约求解过程中的计算时间和存储空间，将计算区域分为CPML区域和非CPML区域 (模拟区域);模拟区域使用常规的波动方程，即f=0的方程式 (21);CPML区域使用CPML波动方程，即带有记忆变量A、B、C'、D'和源项f的方程式(21)和式(24)，在此A、B、C'、D'的时间偏导方程式(16)、式(17)、式(23)、式(24)一同被求解;将不同区域计算方程的各项分别与COMSOL软件所提供的系数形式的PDE时域计算模型式(33)中的对应项进行对比，从而完成对模型中不同求解项系数矩阵(ea质量系数、da衰减系数、c散射系数、α对流流量守恒系数、γ守恒流量源项、a吸收系数、β对流系数)及f源项矩阵的设定，进而完成对方程的有限元求解计算。图3所示是针对于无损流体介质的时域计算结果，为波形在不同时刻t=3.3 μs，6.3 μs，9.3 μs，12.3 μs，15.3 μs 和 27.3 μs 的快照图，从中我们可以定性的看出CPML起到了很好的吸收效果，在边界上没有发生声波的反射。图3(a)～(f)相对于图3(b)的相对最大幅值为分别为 -1.48 dB，0 dB，-3.48 dB，-11.33 dB，-23.78 dB 和 -60.50 dB，从中我们可以看出声波进入CPML吸收层后，声场能量被不断的吸收。图4为测试点A和B的声场在流体介质有损耗及无损耗情况下的声压比较，从中可以看出介质的损耗使得A、B两点的声压分别衰减9.08 dB和12.59 dB。

为了进一步定量分析CPML对损耗流体介质的吸收效果，在此计算了相对误差，其定义为:

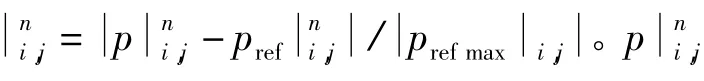
为了探讨CPML层的厚度对波的吸收效果的影响，在此又计算了CPML分别为6层及10层时相对误差随时间变化的规律，如图6所示。其中，当CPML为6个网格厚度时，A、B两点的最大相对误差分别为-66.40 dB 及 -57.72 dB，当 CPML为10个网格厚度时，A、B点的最大相对误差分别为-73.74 dB及-69.05 dB。从而可知增加CPML层的厚度，可以更好地吸收进入其中的声场能量，尤其是更好地吸收倾斜入射的声波能量。为了比较CPML及PML层对入射波吸收效果的不同，在此对10个网格厚度的CPML及PML层的相对误差进行计算，所得A点的最大相对误差分别为-73.74 dB和53.98 dB，B点的最大相对误差分别为-69.05 dB和 -47.47 dB，误差波形变化曲线如图7所示。由此可以看出，无论对垂直入射波还是倾斜入射波，CPML有着比PML更好的吸收效果。

图4 损耗流体及无损耗流体介质的声压在A、B两点的比较Fig 4 Results of comparison for the lossy and lossless media about the pressure field at the points A and B

图5 损耗流体介质中A及B两点的8层CPML的相对误差Fig.5 Relative error at points A and B for 8 cell CPML

图6 A和B两测试点6层CPML及10层CPML的相对误差Fig.6 Relative error at points A and B for 6 cell and 10 cell CPMLs

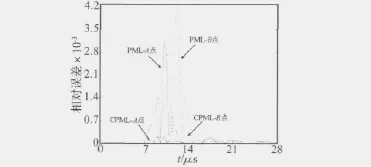
图7 A和B两测试点10层CPML及PML的相对误差Fig.7 Relative error at points A and B for 10 cell CPML and PML

3 结论

本文讨论了卷积完全匹配层(CPML)在吸收流体介质二维声波方程数值计算中的应用，推导给出了二维声波CPML方程在频域和时域的不同表达形式，并在有限元计算软件COMSOL中完成对时域方程的数值求解，给出了取得较好吸收效果的各项参数的数值。

二维数值计算的结果表明对吸收流体介质而言，卷积完全匹配层对进入其中的声场能量起到了很好的吸收效果。对8个网格厚度的CPML层来说，-71.23 dB及-66.10 dB的垂直入射和倾斜入射的相对误差，说明其极大地衰减了进入其中的能量，有效地消除了发生在边界处的反射。通过计算比较6层CPML及10层CPML的相对误差，可知增加CPML的厚度可以更加有效地衰减倾斜入射的声场能量;同时，通过比较可知CPML比PML有着更好的吸收效果，能够更有效地衰减进入声场的能量。

［1］Berenger J P.A perfectly matched layer for the absorption of electromagnetic waves［J］.J.Comput.Phys.，1994，114:195-200.

［2］Gedney S D.Perfeclty matched layer absorbing boundary conditions［C］//Computational Electrodynamics:The Finite-Difference Time-Domain Method.edited by A.Taflove and S.C.Hagness.Norwood:Artech House.2005，273-328.

［3］Chew W C， Liu Q H. Perfectlymatched layersfor elastodynamics:A new absorbing boundary condition［J］.J.Comp.Acoust.，1996，4(4):341-359.

［4］Liu Q H，Tao J.The perfectly matched layer for acoustic waves in absorptive media［J］.J.Acoust.Soc.Am.，1997，102(4):2072-2082.

［5］Hasting F D，Schneider J B，Broschat S L.Application of the perfectly matched layer(pml)absorbing boundary condition to elastic wave propagation［J］.J.Acoust.Soc.Am.，1996，100(5):3061-3069.

［6］Roden J A，Gedney S D.Convolution PML(CPML):An efficient FDTD implementation of the CFS-PML for arbitrary media［J］.Microwave Opt.Technol.Lett.，2000，27:334-339.

［7］Teixeira FL， Chew W C. Generalclosed-form PML constitutive tensorstomatch arbitrarybianisotropicand dispersive linear media［J］.IEEE Microwave and Guided Wave Letters.，1998，8:223-225.

［8］Bécache E，Petropoulos P G，Gedney S D.On the long-time behavior of unsplit perfectly matched layers［J］.IEEE Trans.Antennas Propagat.，2004，52(5):1335-1342.

［9］ Appelö D，Kreiss G.Application of the perfectly matched layer to the nonlinear wave equation［J］.Wave Motion，2007，44:531-548.

［10］Bou Matar O，Preobrazhensky V，Pernod P.Two-dimensional axisymetric numericalsimulation ofsupercriticalphase conjugation of ultrasound in active solid media［J］.J.Acoust.Soc.Am.，2005，118(5):2880-2890.

［11］ Drossaert F H，Giannopoulos A.Complex frequency shifted convolution PML for FDTD modeling of elastic waves［J］.Wave Motion，2007，44(7-8):593-604.

［12］ Komatitsch D，Martin R.An unsplit convolutional perfectly matched Layer improved at grazing incidence for the seismic wave equation［J］.Geophysics，2007，72(5):SM155-SM167.

［13］ Bécache E，Petropoulos P G，Gedney S D.On the long-time behavior of unsplit perfectly matched layers［J］.IEEE Trans.Antennas Propagat.，2004，52(5):1335-1342.

［14］Liu Q H，Chang C.Compressional head waves in attenuative formations:forward modelling and inversion ［J］.Geophysics.，1996，61(6):1908-1920.

［15］ Chew W C，Jin J M，Michelssen E.Complex coordinate stretching as a generalized absorbing boundary condition［J］.Microwave Opt.Technol.Lett.，1997，15:363-369.

［16］ Kuzuoglu M， MittraR. Frequencydependenceofthe constitutive parameters of causal perfectly matched anisotropic absorbers［J］.IEEE Microwave Guided Wave Lett.，1996，6:447-449.

［17］李义丰，李国峰，王 云.卷积完全匹配层在两维声波有限元计算中的应用［J］.声学学报，2010，35(6):601-607.

［18］Li Y F，BouMatar O.Convolutional perfectly matched layer for elastic second-order wave equation［J］.J.Acoust.Soc.Am.，2010，127(3):1318-1327.

［19］ Li Y F，Bou Matar O，Preobrazhensky V，et al.Convolution-Perfectly MatchedLayer(C-PML)absorbingboundary condition for wave propagation in piezoelectric solid［J］.In the Proceedings of 2008 IEEE Ultrasonic Symp.，2008，1568-1571.