考虑涡旋效应的圆柱形TLD多维减震效果研究

何浩祥，闫维明，陈彦江

(北京工业大学 工程抗震与结构诊治北京市重点实验室，北京 100124)

近年来不断发生的强烈地震及其对建筑结构造成的巨大破坏使结构抗震减震和防灾减灾日益受到重视。目前，对于结构在单维地震作用下的分析及设计方面已形成了比较完善的理论，建立了一套有效的抗震设计方法，并在各国抗震规范中均有阐述。然而事实证明，地震动是复杂的空间多维运动，包括三个平动分量和三个转动分量。对于重要的偏心结构，只考虑单维地震作用一般会低估结构实际的动力响应，因此需要考虑多维地震作用对结构的影响［1］。结构在地震作用下，除了产生平移振动外，还会产生不可忽略的扭转振动。引起扭转振动的原因，一是地面运动存在转动分量，或地震时地面各点的运动存在着相位差;二是结构本身存在偏心，即结构的质量中心与刚度中心不相重合［2］。震害表明，扭转作用会加重结构的破坏，在某些情况下将成为导致结构破坏的主要因素。

为了减轻结构在地震下的破坏程度，减震控制技术应运而生。目前基础隔震、消能减振、调谐减振、主动控制等技术针对特定的结构都可以起到减震控制作用［3］。近年来迅速发展的调谐质量或调谐液体减振控制技术由于其无须对结构采取传统的加强措施，且减震效果明显，易于实施，而日益受到广泛重视［4-7］。调谐系统是在结构顶层加上惯性质量或者在附属结构内部添加流动的液体，利用二次系统吸引主体结构的振动能量而使主体结构振动得到控制。调谐液体阻尼器(Tuned Liquid Damper，TLD)具有成本低廉、简单易行、维护费用少、减振效果好的特点，工程应用前景较好。但是调谐质量或调谐液体减振系统目前存在以下不足，主要体现在多维减震的分析方法尚需完善，多维减震效果亟需提高等方面。文献［6］研究了地震作用下利用环形调液阻尼器来控制偏心结构振动的扭转耦联控制方法，在分析中考虑了液体的环流扭转效应。但有关一般圆柱形调液阻尼器的抗扭性能，尤其是液体内部的涡旋形成的抗扭能力在以往研究中往往被忽略。有鉴于此，本文对利用圆柱形调液阻尼器实现偏心结构多维耦联振动控制的力学原理及减震效果进行了研究。结果表明合理布置的调液阻尼器能有效控制结构的平-扭耦联振动，对于严重偏心的结构不能忽略液体涡旋产生的扭转力。

1 基于薄膜法的TLD液动压力模型

调谐液体阻尼器的原理是利用固定在结构上的容器内液体的惯性和粘滞性来达到吸收和消耗结构的动能从而实现减小结构振动的目的。国内外众多研究者提出了不同的简化动力模型来反映TLD的耗能减震特性。Housner［8］曾提出等效质量法，该法将液体晃动产生的对箱壁的液动压力分为脉冲压力和对流压力，并分别用两个与箱体连接形式不同的等效质量的振动效应模拟。Sayar等［9］用摆模型来模拟部分装有水的容器的运动，研究了结构与容器系统的运动。目前应用最广的是利用流体波动力学理论建立的波动模型，主要包括深水模型和浅水模型两种［10］。深水模型适用于水深比大于1/8并且激励幅值和水面晃荡均较小的情况，此时可忽略水的非线性，建立液体线性晃动模型。浅水模型适用范围除了水深应该在1/25～1/20和1/2之间，还应满足激励幅值较小，不出现碎波或碎波较弱的条件。

在上述方法中，等效质量法具有简便易行的特点，并且该法建立的动力模型能够直接与结构动力学方程结合，形成耦联振动体系，进而可以快速求得结构的动力响应。居荣初在文献［8］和文献［11］等研究的基础上，提出了基于薄膜法的液体等效质量模型。

对于浅水容器，其液动压力可以分为脉冲压力和对流压力。脉冲压力与由容器壁的脉冲运动所引起的惯性力相关联，其幅值直接正比于容器壁的加速度，而对流压力则是由于液体晃动所产生的液动压力。

对于具有垂直侧壁和水平底板的容器，若在某一方向的侧壁上施加水平脉冲加速度，则与该侧壁正交方向的加速度可以忽略不计，等价于容器中的液体被若干与底板及施力方向均正交的薄膜所限制。这样，只需考虑薄膜中产生的脉冲压力即可计算出液体的脉冲压力。当容器侧壁承受加速度作用时，液体也会在容器壁和底板上产生液动压力。如果仅考虑液体的第一振型，液体可以被视为水平向可以自由旋转的刚性薄膜。

式中，cs为结构耦合系数，可取0.3～0.6，ρ为液体密度为容器承受的水平加速度;

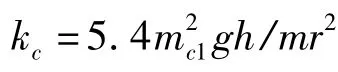
2 基于准均匀涡旋理论的TLD扭转模型

在实际多维地震作用下，安装在结构上的TLD除了在两水平方向上耗能减震外，其内部的液体会产生涡旋现象，可以对结构的扭转进行一定程度上抑制。但目前的TLD动力模型中均没有对涡旋的机理和抗扭效果有所涉及。本文将对此进行研究。

流体力学理论已证明椭球腔是液体能实现均匀涡旋运动的唯一几何形状腔［12］。Pfeiffer［13-15］提出了一种计算非椭球腔内液体流动的近似理论。该理论将流场内各点的涡量平均值近似地描述液体的实际涡量。这种用均匀涡旋运动描述的平均意义下的液体运动，称为准均匀涡旋运动。在实际地震中，圆柱型TLD中的液体的旋转属于非均匀涡旋，因此本文将基于准均匀涡旋理论建立圆柱形TLD的抗扭模型。

全充于任意腔内的理想、不可压缩液体的运动，如果其存在不可忽略的涡旋运动，则引入腔内液体的平均涡量Ωa，其为流场内各点涡量的平均值:

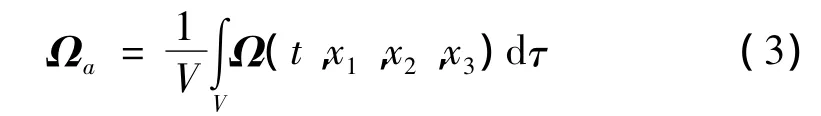
其中V表示液体域的体积。设腔内液体的运动接近于均匀涡旋运动，其速度分布近似地按式(3)写为:

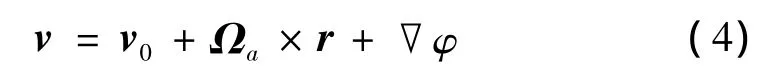
式中，v为流体内任意点P的绝对速度，v0为充液刚体坐标原点的速度，r是流体质点P相对于系统原点的径矢，▽φ为液体的速度势函数。由流体力学理论可知:

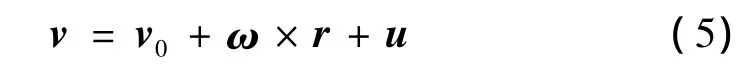
式中，ω为充液刚体的连体坐标系相对于惯性坐标系的转动角速度;u是流体质点P相对于腔体运动的相对速度。相对速度与势函数之间的关系为:

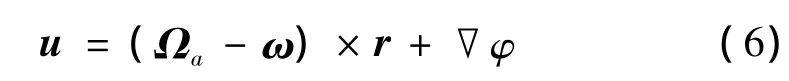
对于均匀涡流运动，有Helmholtz方程:

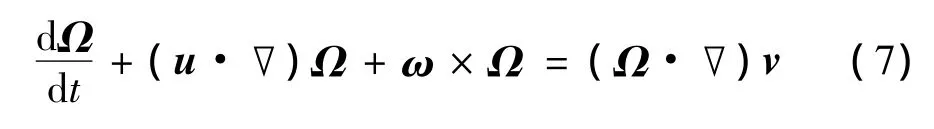
对于任意轴对称腔内的液体，其平均涡量Ωa满足平均化的Helmholtz方程:

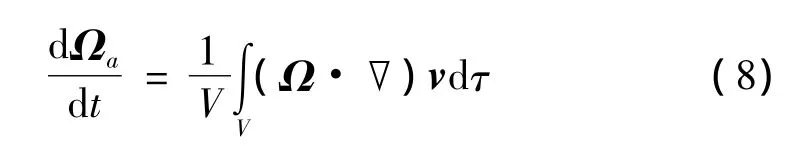
由连续性方程▽·u=0和液体在腔壁上的不可渗透性条件u·n=0，可以导出势函数所满足的方程和边界条件:

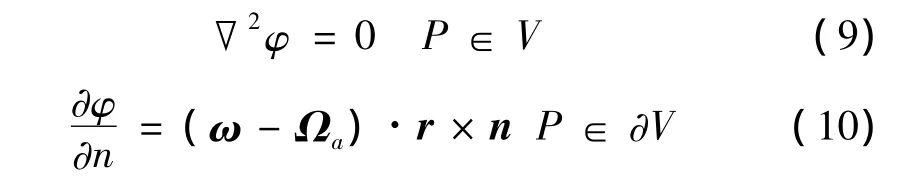
引入Stokes-Rukovskii矢势Ψ，使之满足:

由此，作准均匀涡旋运动的液体的速度式(6)可改写为:

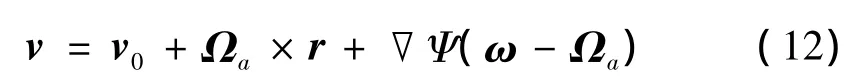
将Helmholtz方程在腔空间内平均化，并将式(12)带入式(8)，可整理得到:

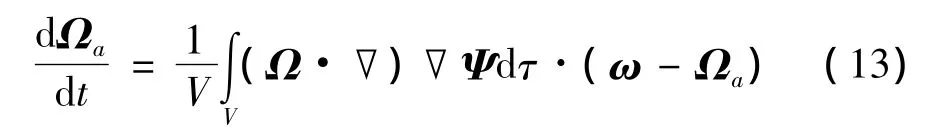
对于旋转对称容腔内液体的准均匀涡旋运动，引入Pfeiffer系数

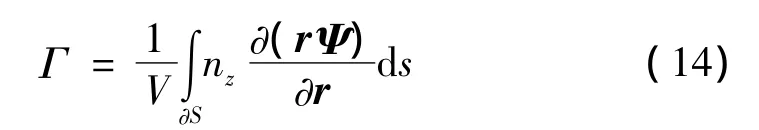
则仅保留线性项的平均化Helmholtz方程变为:

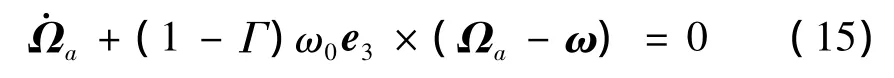
对于半径为r，高为h的圆柱形容腔，其Pfeiffer系数表示为:

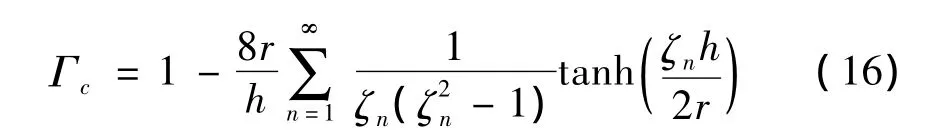
ζn为由第一类一阶Bessel函数关于自变量求导所构成的方程的根。采用分离变量法由对式(8)演变的偏微分方程求解，可以得到圆柱形容腔以其竖向几何中心为主轴的转动惯量为:

由上式即可获得圆柱形TLD的考虑内部液体涡旋效应的整体转动惯量。

3 装有TLD的偏心结构多维动力模型

设在一n层偏心结构的顶层沿纵向和横向设置s个TLD，如图1所示。在两水平向及绕竖轴的扭转向，分别将各层楼板等效为具有单自由度的质点，从而将结构简化为层间模型。该结构体系在多维地震作用下的运动方程为:

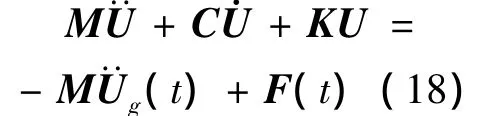
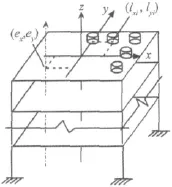
图1 装有TLD的偏心结构模型Fig.1 Eccentric structure model with TLD

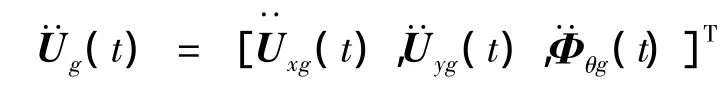
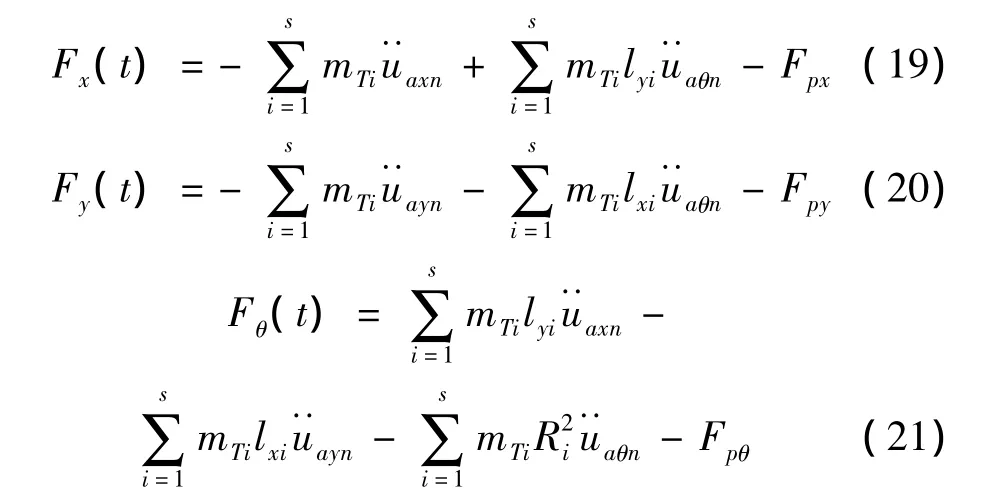
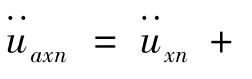
Fpx和Fpy分别表示x向和y向的TLD的液动压力，结合式(1)和式(2)有:

Fpy具有类似的表达式，Fpθ表示考虑涡旋效应的TLD抗扭力，结合式(17)有:

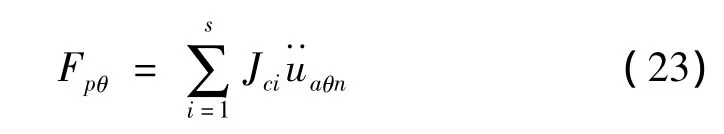
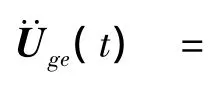
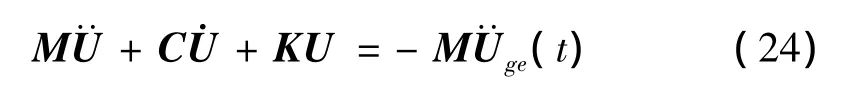
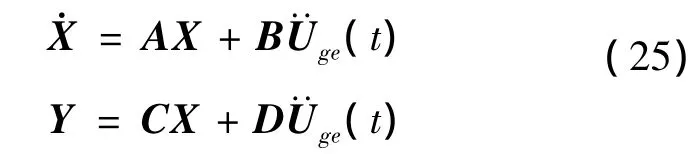
式中:

这样，根据结构加速度激励向量，通过求解系统空间状态方程便可计算得到结构与TLD的耦合动力响应。

4 计算实例

为了验证考虑涡旋效应的圆柱形TLD动力耦合系统的多维减震效果，本文选取一座10层钢筋混凝土框架住宅作为算例。结构平面尺寸为36 m×16.5 m，各层层高均为3 m。柱截面600 mm×600 mm，配筋率为2%。梁截面300 mm×650 mm，配筋率为1.5%。楼板厚120 mm，混凝土强度等级为C40。结构在x向和y向的偏心均为6 m。如图1所示，在结构顶层沿偏心斜对称的两个水平向均匀安装10个圆柱形TLD，每个TLD的半径为2 m，液体高度为1 m。全部TLD的质量为结构整体质量的7.31%。

图2 结构顶层位移减震对比曲线Fig.2 Displacement history comparison of top story

建立层间模型后将El Centro波等地震波作为地震动输入，计算结构的多维地震响应及其减震效果。在El Centro波作用下，是否安装TLD的结构顶层动力响应时程曲线如图2～图4所示，可以看出:安装TLD后，包括位移、加速度和扭转角在内的结构响应都得到一定程度的抑制，TLD的减震效果较为理想。图5和图6分别表示结构整体的位移和扭转减震效果，结果表明TLD对其他层也具有一定的减震效果，但减震率随着楼层号的降低逐渐减弱。

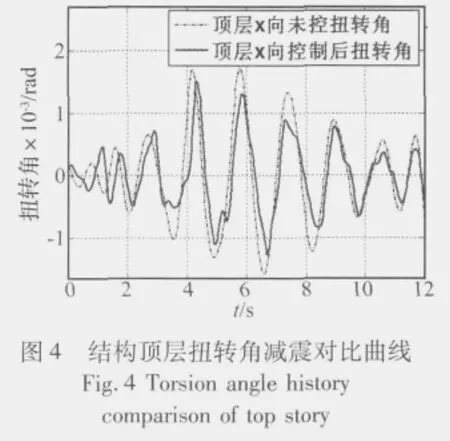
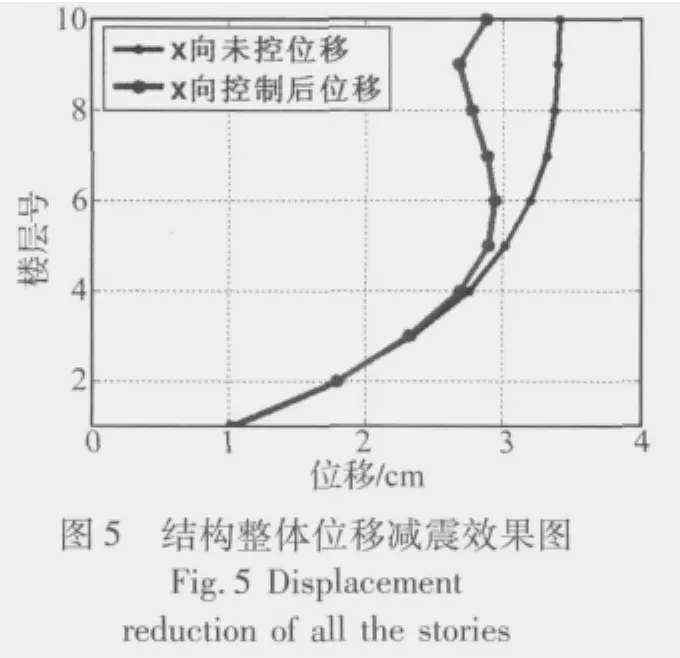
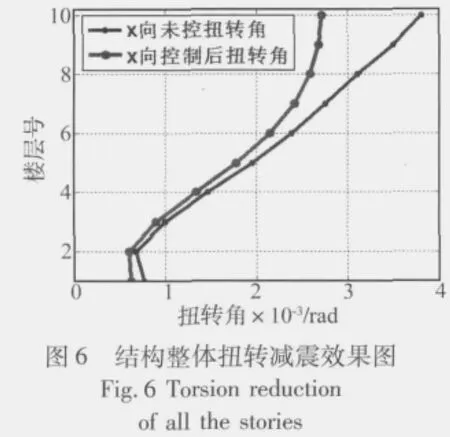
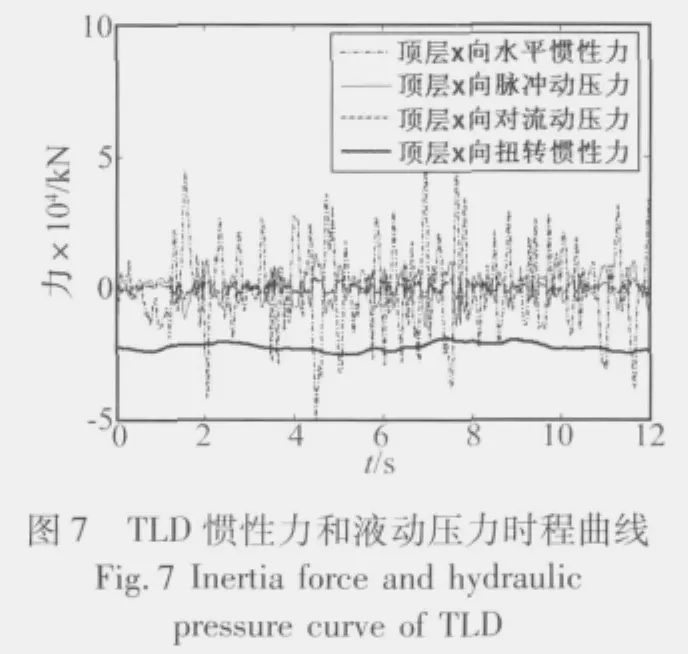
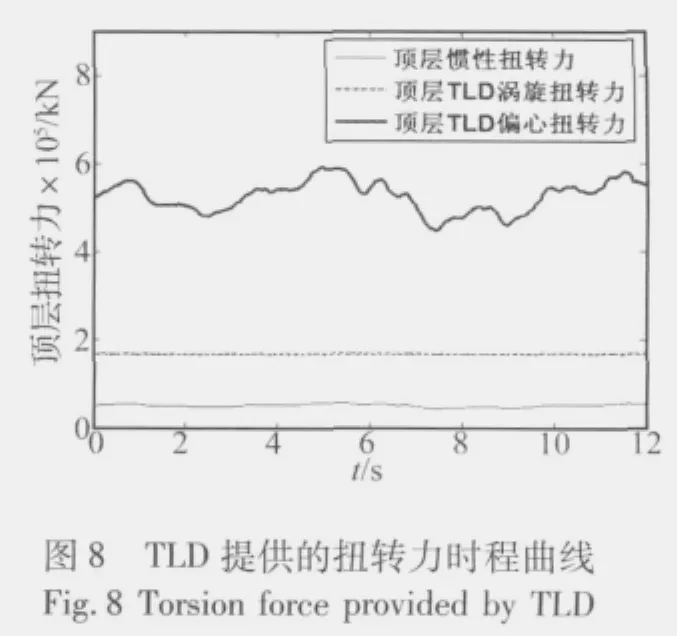
图7为TLD在x向给结构顶层施加的惯性力和液动压力时程曲线，结合式(22)可以看出:TLD产生的偏心惯性力会产生比较稳定且较明显的减震效果，而由TLD提供的脉冲动压力和对流动压力对结构也减震起到了一定的作用。图8为TLD给顶层提供的扭转力时程曲线，结合式(23)可以看出:TLD能够提供给结构的扭转力主要是通过依靠在结构偏心相反方向布置而获得的偏心扭转力，由TLD涡旋效应提供的扭转力也占一定的比例，其作用比由TLD水平惯性力附加成的扭转力要大，在实际减震中不能忽略。

5 结论

本文研究了利用圆柱形调液阻尼器来控制结构在地震作用下的扭转耦联振动。采用薄膜法建立了包含脉冲动压力和对流动压力的调谐液体阻尼器液动压力模型，该模型能够与一般的结构动力方程直接耦合，更适合结构设计使用。基于准均匀涡旋理论获得了考虑调谐液体的抗扭力模型，从而能够考虑调谐液体的自身涡旋效应。建立了考虑偏心扭转效应的结构控制运动方程。以一装有调谐液体阻尼器的偏心结构为算例，对结构在地震作用下的扭转耦联减震效果进行研究，结果表明，由TLD提供的脉冲动压力和对流动压力对结构减震能够起到一定的作用。TLD能够提供给结构的扭转力主要是通过依靠在结构偏心相反方向布置而获得的偏心扭转力，由TLD涡旋效应提供的扭转力也占一定的比例，其作用比由TLD水平惯性力附加成的扭转力要大，在严重偏心结构中需要予以考虑。

［1］De Stefano M，Pintucchi B.A review of research on seismic behaviour of irregular building structures since 2002 ［J］.Bulletin of Earthquake Engineering，2008，6(2):285 – 308.

［2］李宏男.结构多维抗震理论［M］.北京:科学出版社，2006.

［3］周锡元，闫维明，杨润林.建筑结构的隔震、减振和振动控制［J］.建筑结构学报，2002，23(2):2-12.

［4］Jangid R S，Datta T K.Performance of multiple tuned mass dampers for torsionally coupled system ［J］.Earthquake Engineering and Structural Dynamics，1997，26(3):307-317.

［5］李春祥.多重调谐质量阻尼器控制单层非对称结构扭转振动的设计参数［J］.振动与冲击，2005，24(1):118-120.

［6］霍林生，李宏男.调液阻尼器对偏心结构扭转耦联振动控制的研究［J］.工程力学，2010，27(1):84-90.

［7］居容初，曾心传.弹性结构与液体的耦联振动理论［M］.北京:地震出版社，1983.

［8］Housner G W.Dynamicpressureonacceleratedfluid containers［J］.Bulletin of the Seismological of America，1957，41(1):15-35.

［9］ Sayar B A，Baumgarten J R.Linear and nonlinear analysis of fluid slosh dampers［J］.AIAA Journal，1982，20(11):1534-1538.

［10］ Yalla S K.Liquid dampers for mitigation of structural response:Theoretical development and experimental validation［D］.University of Noire Dame，Indiana，2001.

［11］ Epstein H I.Seismic design of liquid storage tanks ［J］.Journal of Structural Division，1976，102(9):1659-1673.

［12］王照林，刘延柱.充液系统动力学［M］.北京:科学出版社，2002.

［13］包光伟.自旋液体晃动Pfeiffer方法的分析［J］.力学学报，1993，25(6):738-743.

［14］丁遂亮，包光伟.任意三维贮箱内液体晃动的模态分析及其等效力学模型［J］.力学季刊，2004，25(1):62-68.

［15］包光伟.微重力环境下慢自旋充液容器内的液体晃动［J］.力学季刊，1992，13(4):19-27.