冲击载荷作用下金属圆柱壳能量吸收研究

戴向胜，马建敏

(复旦大学 力学与工程科学系，上海 200433)

金属圆柱壳是有效的吸能结构之一，能在有限的压缩空间内产生塑性变形而吸收大量的能量，可以取得一般减振器所不能得到的减振效果，因此很多学者对此进行了研究，Alexander［1］提出了静态塑性铰模型，该模型是基于金属圆柱壳的最终破坏模式提出的，假定所有的塑性铰同时形成.而不考虑屈曲的过程，同时假设金属圆柱壳的能量吸收有两个部分，一个是弯曲变形能，另一个是拉伸变形能和压缩变形能。Abramowicz和Jones［2］在研究中考虑了瞬时几何构型，并且提出有效压缩长度的概念，同时还考虑了冲击载荷的应变率效应和应变强化效应。Wierzbicki和Bhat［3］提出了直链塑性铰模型，并根据模型模拟出载荷-位移曲线，并且提出偏心率效应，并给出不同偏心率的载荷-位移曲线，但其研究结果表明偏心率对吸能效率没有影响。Singace［4］认为吸能效率与偏心率有关，并给出最优偏心率，给出了塑性铰长度和平均压缩载荷。Karagiozova［5-7］应用有限元研究了低速冲击和高速冲击下的金属圆柱壳的响应历程。

上述文献中没有考虑到在冲击载荷作用下的温度效应，在该效应的作用下材料的应力应变关系会随着金属圆柱壳叠缩的进行而发生相应的变化，从而导致金属圆柱壳吸收能量的计算结果不一样，本文利用粘塑性理论在考虑温度效应下对圆柱壳的吸能情况进行研究，提出分步叠缩法计算塑性变形能，并且得到该种情况下的载荷位移曲线，为实际工程运用给出了一种金属圆柱壳吸收能量的理论计算方法以及金属圆柱壳减振效果的判断依据。

1 模型的建立

1.1 几何模型

塑性金属圆柱壳的轴向压缩破坏模式主要有轴对称叠缩模式和非轴对称叠缩模式。而破坏模式主要由直径壁厚比决定，直径壁厚比较大的发生非轴对称破坏，反之发生轴对称破坏，后者的比吸能一般较大，且破坏模式相对稳定。非轴对称模式属于一种局部的失稳，轴压载荷不易预报，现有研究主要是针对发生轴对称破坏模式的金属壳进行吸能特性的研究，本文所研究的圆柱壳直径壁厚比符合轴对称叠缩模式，而且金属圆柱壳所受冲击载荷是轴对称的，因此假设所产生的变形也是轴对称的;在冲击载荷的作用下，整个圆柱壳根据冲击载荷的大小、圆柱壳材料特性以及圆柱壳形状的不同而发生不同的叠缩模式，本文主要研究发生如图1所示叠缩过程的情况，该模型是在Singace模型［4］的基础上提出的，整个叠缩过程分为两个阶段，依次为内翻(Ⅰ)和外翻(Ⅱ)。

1.2 前提假设

(1)金属圆柱壳所受冲击载荷是轴对称的，并且所产生的变形也是轴对称的。

(2)整个叠缩过程绝热的，冲击载荷所作的功大部分转为弯曲变形能和伸张变形能，其中伸张变形能是管壁沿周向方向受拉伸或压缩而做功，弯曲变形能是塑性铰在塑性弯矩的作用下发生弯曲所做的功。

(3)在冲击载荷作用下金属圆柱壳中热量传导在瞬时完成。

1.3 材料本构的选择

因为金属圆柱壳在冲击载荷的作用下是大变形、高应变率和高温条件下的流变行为，所以选择Johnson-Cook本构［8］，该本构是由Johnson和Cook于1983年在位错动力学的基础上提出的一个适用于金属大变形、高应变率和高温条件下流变行为的本构方程，其优点是形式简单、使用方便。Johnson-Cook本构的方程公式是:

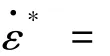
2 塑性变形能的计算方法

整个过程是绝热的，冲击载荷所作的功大部分转为热量;这些热量导致材料的温度升高从而发生材料的温度软化效应，为了把该温度效应考虑进去，根据图1中的角度(α和φ)的增加量把整个叠缩过程分为N步，即每个叠缩时图1中的角度(α和φ)变化量是α0/N和φ0/N，而整个塑性变形能是每个叠缩的塑性变形能之和。

在计算第I个叠缩时金属圆柱壳所吸收能量时，因为在第1个到第I-1个叠缩每个叠缩完成时载荷所作的塑性功会使得材料的温度上升，即公式(1)中的T发生变化，材料的σp也发生相应的变化，所以在计算第I个叠缩的塑性变形能时，应使用变化之后的等效应力应变关系，T的计算方法见公式(16)。

2.1 塑性变形能计算

在第I个叠缩中的变形能包括弯曲变形能和伸张变形能两个部分，以下是这两个部分的计算方法:

2.1.1 第I个叠缩中弯曲变形能计算

在叠缩过程中有三个塑性铰，每个塑性铰的应变率不同，所以相应的等效塑性应力也不同，因此计算公式分别是:

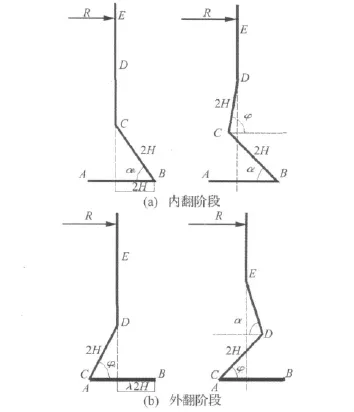
图1 圆柱壳的叠缩过程Fig.1 The fold formation of the tube

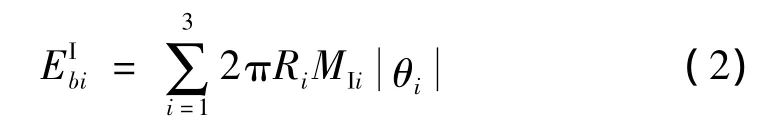
式中在i=1，2，3时分别对应图1中的塑性铰B，C，D;Ri是三个塑性铰沿着圆柱壳半径方向的发生变形之后到轴线的距离，MIi是三个塑性铰单位长度全塑性弯矩，θi是三个塑性铰转动角度;

对应的三个塑性铰式中的参数分别是:

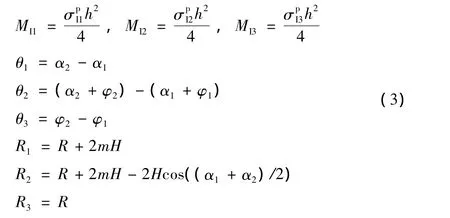
在圆柱壳塑性变形中沿着厚度方向的应变远小于其它两个方向的应变，并且在薄壳理论中有切平面应力假设，因此可以假设沿着厚度方向应变为零;对塑性变形可以假设塑性体积在变形的过程中是不变的从而有:ε1+ ε2+ ε3=0;式中 ε1、ε2、ε3分别是塑性铰所在的部分的三个主应变;

ε1是沿着圆柱壳周长方向的应变;ε2是沿着圆柱壳长度方向的应变;ε3是沿着圆柱壳厚度方向的应变，所以有:

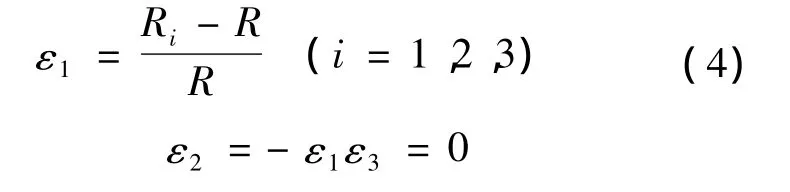
式中R是圆柱壳原始半径;在i=1，2，3 时，ε1、ε2、ε3分别对应的是三个塑性铰B、C、D的三个主应力。

根据等效塑性应变的计算公式，则第I个叠缩中的三个塑性铰B、C、D的等效塑性应变分别是

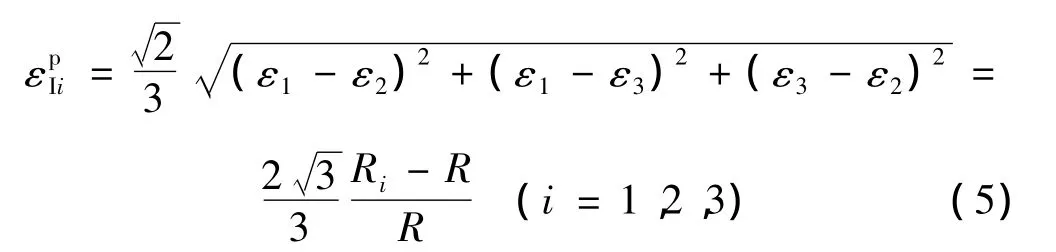
在i=1时对应是塑性铰B所在的部分的等效塑性应变;在i=2时对应是塑性铰C所在的部分的等效塑性应变;在i=3时对应是塑性铰D所在的部分的等效塑性应变。

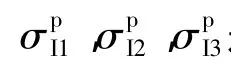
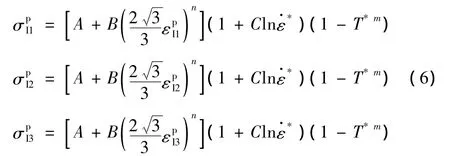
其中T*中所使用到的TI是根据式(16)得到的;是金属圆柱壳的平均应变率［9］，该参数是根据下式计算得到:

式(7)中的是金属圆柱壳在叠缩过程中的平均叠缩速度;

叠缩长度［4］H是根据下式计算得到:

综上有第I个叠缩中弯曲变形能是:

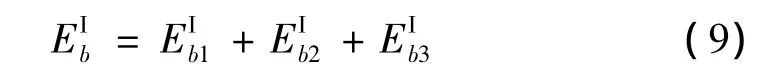
2.1.2 第I个叠缩中的伸张变形能

整个的叠缩包括BC段和CD段，设微元 dl是沿BC段和CD段线段方向上的微元，则该微元所吸收的伸张变形能计算公式是:

则BC段所消耗的伸张变形能则是:

CD段所消耗的伸张变形能则是:

则第I个叠缩中伸张变形能是BC段和CD段所消耗的伸张变形能之和，所以根据式(11)和式(12)有:

2.1.3 第I个叠缩所吸收的总能量

根据式(9)和式(13)，可以得到图1中第I个叠缩中总能量是:

2.2 第I个叠缩中冲击载荷导致温度升高值

在高应变率、大变形的情况下，温度的升高可用下式进行计算［10］:

式中:ρ为材料密度、Cv为比热容、εp为等效塑性应变、σp为等效塑性应力、β≈0.9为塑性功转化为试件温升的比例，γ1和γ2分别是第I个叠缩的等效塑性应变的下限(终止)值和上限(开始)值，在计算时等效塑性应变分别取BC段和CD段中点的塑性应变。

则第I-1个叠缩中冲击载荷导致温度升高值是ΔT，则在计算第I个叠缩时所使用的温度是TI:

3 叠缩过程中的平均载荷和瞬时载荷

3.1 叠缩过程中的平均载荷

可以利用计算得到的整个过程的总变形能和圆柱壳端点的垂直位移计算叠缩过程中的平均载荷:

E是整个过程的总变形能，δ是圆柱壳端点的垂直位移。

3.2 叠缩过程中的瞬时载荷

可用第I个叠缩中变形能的增加量ΔE(I)和位移的变化量Δδ(I)计算第I个叠缩中瞬时载荷:

所有叠缩中的瞬时载荷就是整个变形过程中的瞬时载荷，通过上式可以得到瞬时载荷-位移曲线，而依据该曲线即可判断减振效果，瞬时载荷的最大值越小减振效果越好，曲线越平缓减振效果越好。

4 铝合金圆柱壳算例

根据本文提出的塑性变形能的计算方法，对材料是2024Al铝合金圆柱壳进行计算，其参数如下:

Johnson-Cook本构参数:A=218 MPa、B=546 MPa、C=0.038、m=3.73、n=0.355;(2)几何参数是:内径49.5 mm、外径50.5 mm、平均直径50 mm、半径25 mm;壁厚1 mm、偏心率λ=0.65，计算结果如下:

(1)不同的冲击速度下铝合金圆柱壳在叠缩过程中所吸收的能量(见图2)

从图中可以得到总的能量随着冲击速度的不同而不同;当冲击速度是5 000 m/s时是285J，而不考虑冲击载荷效应的是108J。

(2)不同的冲击速度下铝合金圆柱壳在叠缩过程中温度的增加值(见图3)

从图中可以得到随着冲击速度的增加，圆柱壳在叠缩过程中温度的增加值也是增加的。

(3)不同的铝合金圆柱壳厚度下叠缩过程中所吸收的能量(见图4)

(4)不同的铝合金圆柱壳半径下叠缩过程中所吸收的能量(见图5)

(5)铝合金圆柱壳叠缩过程中的平均载荷和瞬时载荷

① 叠缩过程中的平均载荷

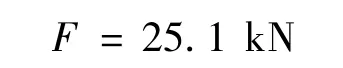
而不考虑冲击载荷效应的平均载荷是8.6 kN。

② 叠缩过程中的瞬时载荷(见图6)

5 结论

(1)金属圆柱壳在冲击载荷的作用下(材料假设为粘塑性材料)其叠缩过程中总的吸收能量、平均载荷以及瞬时载荷-位移曲线都比把载荷假设为准静态(材料假设为刚塑性)的数值更大，从而和实际更为接近;

(2)金属圆柱壳所吸收的能量和叠缩过程中的速度、金属圆柱壳的厚度、半径有关;金属圆柱壳的叠缩过程中的速度越大，金属圆柱壳的厚度越大、半径越大，所吸收的能量越大。

［1］Alexdaner J M.Appromixmate analysis of the collapse of thin cylindrical shell under axial loading［J］.Q.J.Mech.appl.Math，1960(13):10-15.

［2］Abramowicz W，Jones N.Dynamic progressive buckling of circular and square tubes［J］.International Journal of Impact Engineering，1986，(4):243-270.

［3］Wierzbicki T，Bhat S U.A moving hinge solution for axisymmteic crushing of tubes［J］.Int J of Mech.Sci，1986(28):135-151.

［4］Singace A A，Elsobky H，Reddy T Y.On the eccentricity factor in the progressive crushing of tubes［J］.International Jorurnal of Solids and Structures，1995(32):3589-3603.

［5］Karagiozova D，AlvesM，JonesN. Intertia effectsin axisymmtrically deformed cylindrical shells under axial impact［J］.International Journal of Impact Engineering，2000(24):1083-1115.

［6］ Karagiozova D，Jones N.Dynamic elastic-plastic buckling of circular cylindrical shells under axial impact international［J］.Journal of Solids and Structures，2000(37):2005-2034.

［7］Karagiozova D，Jones N.Dynamic effects on buckling and energy absorption of cylindrical shells under axial impact［J］.Thin-Walled Structures，2001(39):583-610.

［8］ Johson G R，Cook W H.A constitutive model and data for metals subjected to large strains，high strain rates and high temperatures［C］.Proceedings of the Seventh International Symposium on Ballistics，1983:541-547.

［9］ Abramowicz W，Jones N.Dynamic axial crushing of circular tubes［J］.International Journal of Impact Engineering，1984，2(3):263-281.

［10］ Nemat-Nasser S. ThermomechanicalresponseofDH-36 structural steel over a wide rangeofstrain ratesand temperatures［J］.Mechanics of Materials，2003，35:1023-1048.