非连续粗糙多界面接触变形和能量损耗特性研究

肖会芳，邵毅敏，周晓君

(重庆大学 机械传动国家重点实验室，重庆 400030)

动力系统中，结构之间通过界面进行动力耦合和能量传递。由于动力系统结构的复杂性，往往是多结构，非连续多界面的相互耦合与相互作用。同时，实际工程结构表面，并非绝对平面，而是具有不同程度的粗糙度［1-4］。振动与能量经过这些非连续的粗糙多界面时，具有怎样的损耗行为与传递机理，对描述动力系统的振动特性与能量特性至关重要，也是研究较少的难题。

本文在对非连续单一结构界面的变形与能量损耗进行研究的基础上［5］，通过建立“多层粗糙金属板-刚性平面”的多界面模型，采用有限元方法，对加载与卸载过程中，具有不同粗糙界面形貌、不同塑性变形-硬化行为和界面摩擦的多层叠加模型多界面的接触力和变形进行计算，分析了多层叠加结构非连续多界面的塑性变形及硬化引起的能量损耗，讨论了能量在多界面传递时沿接触界面的损耗特性，以及界面摩擦对塑性变形-硬化引起的能量损耗的影响。

1 “多层粗糙金属板－刚性平面”模型

1.1 模型描述

螺栓连接是机器设备最主要的零部件连接方式之一，在不同零部件的结合面产生的振动能量耗散占机器设备总能量耗散的比率高达80% ～90%［6］。螺栓连接是典型的非连续粗糙多界面接触形式。其中，两个部件配合紧固垫圈通过螺栓进行连接，是其最广泛的连接方式之一，具有三部件-四接触界面特征。本文提出的多层叠加结构粗糙界面接触的“多层粗糙金属板-刚性平面”模型，如图1所示。其中，三层金属板纵向叠加置于固定的下刚性平面，金属板的表面为具有一定表面形貌的三维粗糙表面。法向外载荷施加于上部可移动的刚性平面。图1所示模型的接触界面分别为1，2，3 和 4。其中，界面1和界面4是金属板1和金属板3分别与上、下刚性平面的接触面;界面2和界面3是金属板1与金属板2，金属板2与金属板3的接触面，并假设各层金属板的材料属性相同。

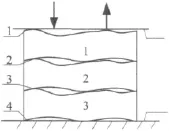
图1 “多层粗糙金属板-刚性平面”多界面模型示意图Fig.1 Sketch diagram of“multiple rough plates-rigid plane”model

结构的表面粗糙度可以通过统计学参数进行表征和描述［1，2］，如表面高度的标准偏差 σ，斜率 σ'和曲率σ″，其参数依赖于样本的尺寸和测试仪器的精度，具有尺度依赖性。与统计学参数模型相比，表面分形模型具有自相似和尺度独立的特性，更能从本质上描述粗糙表面的特征［7-9］。三维分形表面可以通过修正的两参数 Weierstrass– Mandelbrot函数生成［10-11］:

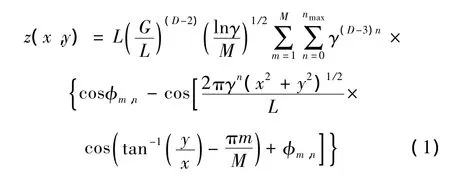
其中，L为样本长度，G为分形粗糙度，D为表面分形维数(2＜D＜3)，Ls为截断长度，γ (γ ＞1)为缩放参数，M为生成分形表面的脊线数量，n是频率因子，nmax=int［log(L/Ls)/logγ］，Φm，n是［0，2π］内的随机相位。

表面粗糙程度由尺度独立的分形参数D和G控制。表面分形维数D，其物理意义是粗糙表面所占据的空间程度大小，D值越大对应于越密集的表面形态(更光滑的表面形貌)。表面分形粗糙度G是高度尺度参数，G值越大对应于越粗糙的表面形貌。参数D和G一般通过实验测试确定。根据实验结果，D的范围为［2.3，2.7］，G的范围为［1.36e-13，1.36e-10］m［10］。

式(1)所示的粗糙表面高度函数具有比例不变和自相似特性，即:在表面粗糙度一定时(D和G值一定)，不同样本长度L表征的表面具有相似的形貌特征［10］。本文以 Weierstrass-Mandelbrot函数生成的 0.9 μm×0.9 μm各向同性三维分形表面进行多界面的接触变形和能量损耗特性研究，其分形表面形貌如图2所示。其中，Ls=1.5e-7m，M=10，γ =1.5［11］，G=1.36e-11m，图2(a)的D=2.3，图2(b)的D=2.7。图2显示，对相同的表面分形粗糙度G，增大分形维数D的表面形貌更光滑。

图2 不同表面粗糙度的三维分形粗糙表面(G=1.36e-11m)Fig.2 Three-dimensional Weierstrass-Mandelbrot fractal surfaces(G=1.36e-11m)

本文主要研究粗糙金属板与刚性平面之间，以及粗糙金属板与粗糙金属板之间的弹-塑性接触行为。在粗糙表面，实际接触面积远小于整个粗糙表面面积，接触面仅为一些点和很小的面，因而很容易在接触点处发生应力集中，使应力值高于屈服应力而产生塑性变形［5，12］。塑性变形不可恢复，可以通过金属板弹塑性材料的屈服准则和硬化准则来计算［12］。不同硬化准则的应力-应变关系如图3所示，包括线性应变硬化(LH)，非线性应变硬化(NLH)和理想弹塑性(EPP)，对应于不同的塑性变形-硬化行为。线性应变硬化(LH)准则的应力-应变关系为:

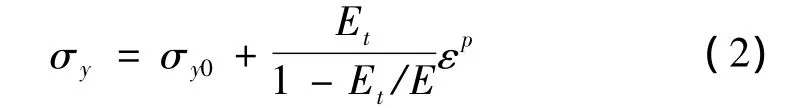
非线性应变硬化(NLH)的应力-应变关系为:

其中，σy0为初始屈服应力，E为弹性模量，Et为剪切模量，εp为塑性应变，r0，r∞，b为非线性硬化准则对应的常数。理想弹塑性(EPP)的应力-应变关系对应于式(2)中Et=0。

图1所示模型的移动刚性平面施加均布的法向位移，位移逐渐加载到最大值后卸载，计算加载与卸载过程中不同界面处的变形和接触力，并绘制接触力-变形曲线，曲线形成封闭区域的面积即为该界面的能量损耗U。能量在多界面进行传递时沿接触界面的损耗特性通过能量传递损耗率η描述，界面i的能量传递损耗率ηi定义为:

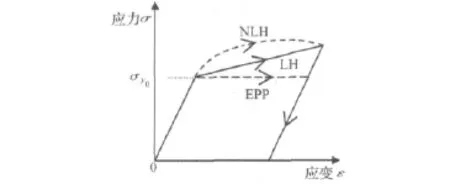
图3 不同硬化准则的应力应变关系，线性应变硬化(LH)，非线性应变硬化(NLH)和理想弹塑性(EPP)Fig.3 Stress strain relationships，linear hardening(LH)，nonlinear hardening(NLH)，and elastic-perfectly plastic(EPP)

其中，Ui为界面i(i=1，…，N)的能量损耗量，UT为所有界面的总能量损耗量，UT=∑Ui，在图1所示模型中，N=4。ηi为界面i的能量损耗占总能量损耗的比值。

1.2 有限元计算模型

有限元计算模型，如图4所示。其中，图4(a)和图4(b)的粗糙界面分别与图2(a)和图2(b)所示的三维分形粗糙表面对应。有限元模型的建立方法与文献［5］一致，即:金属板用SOLID185单元离散;金属板与刚性平面之间，金属板和金属板之间建立接触对;底部刚性平面全约束，上刚性平面仅具有Z方向自由度;均布的位移载荷通过加载和卸载两个载荷步施加在上刚性平面;求解金属板与刚性平面之间，金属板与金属板之间的接触力;绘制不同界面的接触力-变形曲线。文献［5］已对有限元计算方法的有效性进行了验证，本文不再赘述。为叙述简便，模型(a)的界面简称为:形貌Ⅰ界面，模型(b)的界面简称为:形貌Ⅱ界面。

图4 有限元计算模型Fig.4 Finite element mesh of rough solid and rigid plate

2 计算结果与分析

计算采用的材料参数与文献［5］一致，如表1。对各接触界面(界面1，2，3和4)的法向接触力Fn和变形量z进行无量纲化处理:fn=Fn/E'A0，δ=z/L，其中A0为名义接触面积(=L2，L为样本长度)，E'为复合弹性模量(E'=E/(1-ν2)，E为弹性模量，ν为泊松比)。

表1 材料参数Tab.1 Material parameters used in calculations

2.1 界面无摩擦

2.1.1 接触力-变形关系(fn-δ曲线)

界面无摩擦，金属板的塑性变形行为不同，最大法向变形δ=0.1，不同界面形貌(形貌I界面(a)和形貌II界面(b))，加载和卸载过程，界面1、2、3和4的力-变形关系曲线，如图5所示。

与单一界面相同［5］，各接触界面的加载和卸载曲线也存在滞回面积。加载过程，各界面的接触力随变形呈非线性增加，接触刚度为非线性;不同形貌界面的接触刚度随变形的变化规律不同:对形貌I界面(D=2.3，图5(a)、(c)、(e))，接触刚度随变形的增大由初始值零逐渐增大(曲线斜率由零逐渐增大);而对更平滑的形貌 II界面(D=2.7，图5(b)、(d)、(f))，最大接触刚度为初始接触阶段，载荷逐渐增加，接触刚度逐渐减小(曲线斜率逐渐减小)，当变形增大到一定数值后，刚度几乎保持不变(曲线斜率为定值)。卸载过程，接触力随变形递减，接触刚度逐渐减小。加载和卸载过程，不同界面的接触刚度大小不同，界面4的接触刚度最大(曲线的斜率最大)，界面1最小。

加载过程，对形貌 I界面(D=2.3)，不同界面i(i=1，…，N，N=4)的接触力与变形可用关系式(5)表示:

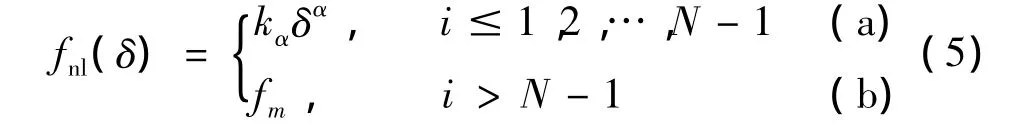
加载过程，对形貌Ⅱ界面(D=2.7)，不同界面i(i=1，…，N，N=4)的接触力-变形关系可表示为指数非线性、线性项、二次非线性和三次非线性之和，可由式(6)表示:

其中，式5(a)和式6(a)用于描述界面1，2和3的力-变形关系，系数kα和 α、kβ、β、k1、k2和k3，与界面形貌、界面的材料属性和接触界面的位置相关。

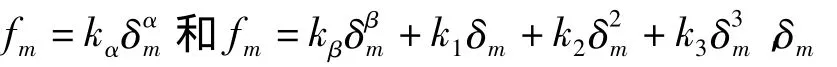
图5 无摩擦时不同界面形貌和材料属性下各界面加载与卸载的力-变形曲线Fig.5 Plots of force vs.deformation at different interfaces of different material models

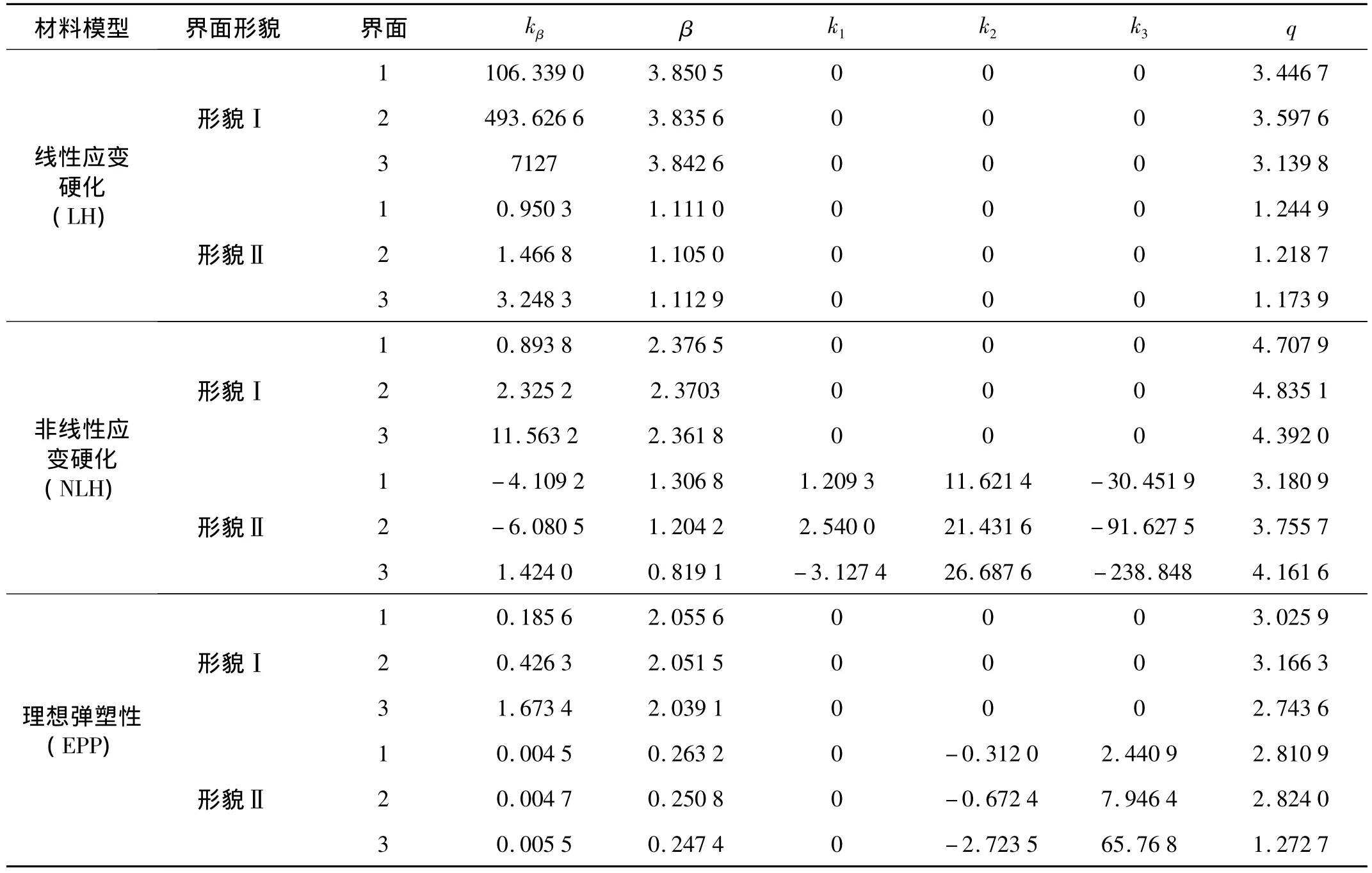
表2 力－变形关系表达式的系数表Tab.2 Coefficients of kβ，β，k1，k2and k3in Eq.(6)，q in Eq.(7)for varying cases studied

卸载过程，不同界面i(i=1，…，N，N=4)的接触力-变形关系可表示为:

其中，式7(a)用于描述界面1，2和3的力-变形关系，δp为塑性变形量，q为非线性指数。因界面4的卸载接触力瞬时减小为零，其接触力如式7(b)。

图5的结果表明:式(6)和式(7)能很好地描述各界面的力-变形关系，表达式中的各系数数值，如表2所示。为验证力-变形关系表达式(6)和式(7)的有效性，对比了金属板具有理想弹塑性变形行为且界面形貌为形貌Ⅱ界面时(图5(f))的力-变形关系式与实际计算结果之间的相对误差，如图6所示。最大相对误差是13.2%，出现在变形初始阶段;其余部分的相对误差值约为3%，图6所示的结果表明式(6)和式(7)可以有效表征实际计算结果，具有较高精度。

图6 力-变形关系计算式与实际计算值的相对误差Fig.6 Plot of relative error between calculated results and results obtained using Eq.(6)and Eq.(7)

2.1.2 能量传递损耗率-变形关系(η-δ曲线)

图5显示，界面1，2，3和4加载曲线和卸载曲线形成的滞回面积大小不同，界面1最大，界面4最小。滞回面积的大小即为能量损耗量，表明界面1能量损耗最大，界面4最小。不同接触界面的能量损耗量Ui可表示为:

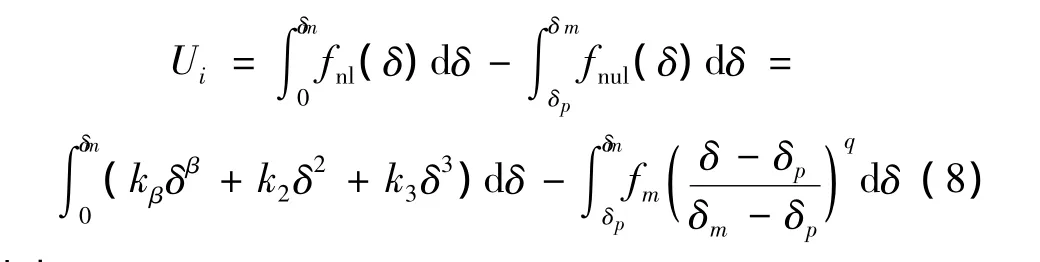
其中:

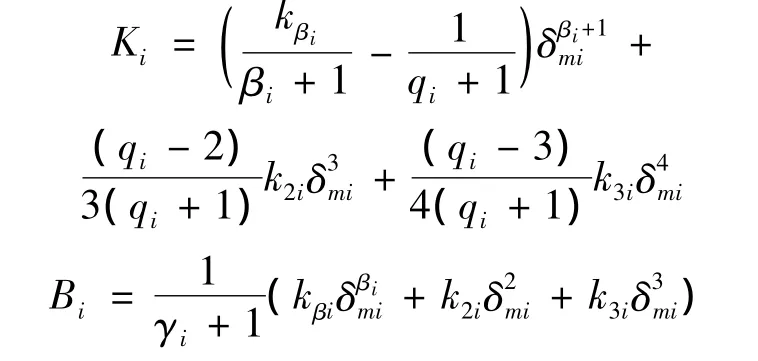
式(8)显示，在界面属性和最大变形量一定时，界面能量损耗量U随着塑性变形的增加呈线性递增。式(8)与式(4)可用于计算不同界面处的能量传递损耗率ηi。

界面无摩擦，不同塑性变形行为(线性应变硬化(LH)，非线性应变硬化(NLH)和理想弹塑性(EPP))，不同界面形貌(形貌Ⅰ界面和形貌Ⅱ界面)，各界面(界面1，2，3和4)的能量传递损耗率-变形关系曲线(η-δ曲线)，如图7所示。

图7显示，形貌I界面(图7(a))，界面 1，2，3的能量传递损耗率 η几乎不随材料属性(LH，NLH和EPP)变化，而界面4的能量传递损耗率η受材料属性影响较大;不同界面的能量传递损耗率η随变形量δ变化:随着变形δ增大，界面1的能量传递损耗率减小;界面2几乎不变;界面3和界面4增大。其中，界面1的能量传递损耗率η最大，η≈0.5;界面2的能量传递损耗率η≈0.33;界面 3的能量传递损耗率约为η≈0.16;界面4 最小，η≈0.07。

表3 无摩擦与有摩擦的力－变形关系表达式系数对比Tab.3 Coefficients of kβ，β，k1，k2and k3in Eq.(6)，q in Eq.(7)for cases studied with and without friction

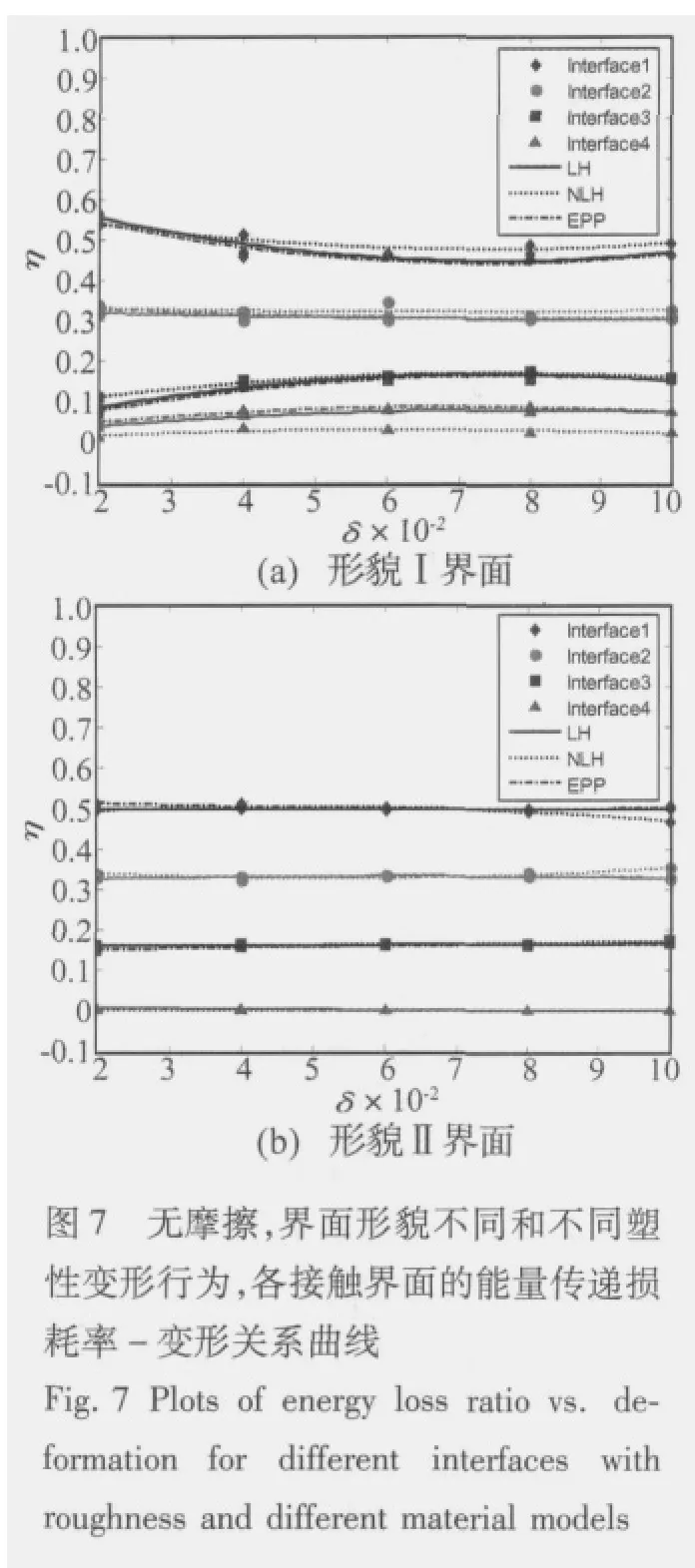
对更平滑的形貌Ⅱ界面(图7(b))，不同界面(界面1，2，3和4)的能量传递损耗率η几乎不随材料属性和变形量δ而变化。与形貌Ⅰ界面一致(图7(a))，形貌Ⅱ界面(图7(b))在界面1的能量传递损耗率η最大，界面4最小;但与形貌Ⅰ界面的界面4处η≈0.07不同，在形貌Ⅱ界面的界面4处η≈0，即最后接触界面的能量损耗几乎为0。

图7表明对非连续的粗糙多界面，由塑性变形引起的能量损耗，约有50%损耗在第一接触界面，约有33%损耗在第二接触界面，而最后界面的能量损耗最小，几乎为0。

2.2 界面存在摩擦

实际界面一般存在摩擦，界面存在摩擦时的有限元计算模型与2.2节相同，不同的是在接触界面处增加了摩擦因子μ=0.2。金属板的塑性变形行为为非线性应变硬化(NLH)，重点讨论界面摩擦对其界面力-变形关系，以及能量耗散的影响。

2.2.1 接触力-变形曲线

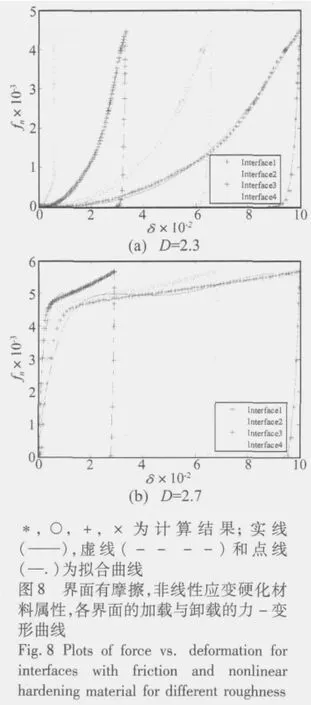
界面存在摩擦，金属板具有非线性应变硬化材料属性，最大变形为δ=0.1，形貌Ⅰ界面(a)和形貌Ⅱ界面(b)，加载和卸载过程，各界面的力-变形关系曲线，如图8所示。与图5界面无摩擦的曲线相比，界面存在摩擦时:力-变形曲线形状基本一致，因而各界面的接触刚度变化趋势一致;相同变形下，各界面的接触力增大，因而其界面能量损耗量增大［5］。但与无摩擦相比，各界面滞回面积大小的比例并无明显变化。

图8的拟合曲线显示，式(6)和式(7)同样很好地描述了界面存在摩擦时，加载和卸载过程，不同界面的力-变形关系，表达式(6)和式(7)中各系数的数值如表3所示。表3显示，与无摩擦的系数相比，界面存在摩擦时:系数kβ和非线性指数β基本均增大，卸载曲线的非线性指数q减小，而线性项系数k1，二次和三次非线性项系数k2和k3并无变化规律。

2.2.2 能量传递损耗率-变形曲线

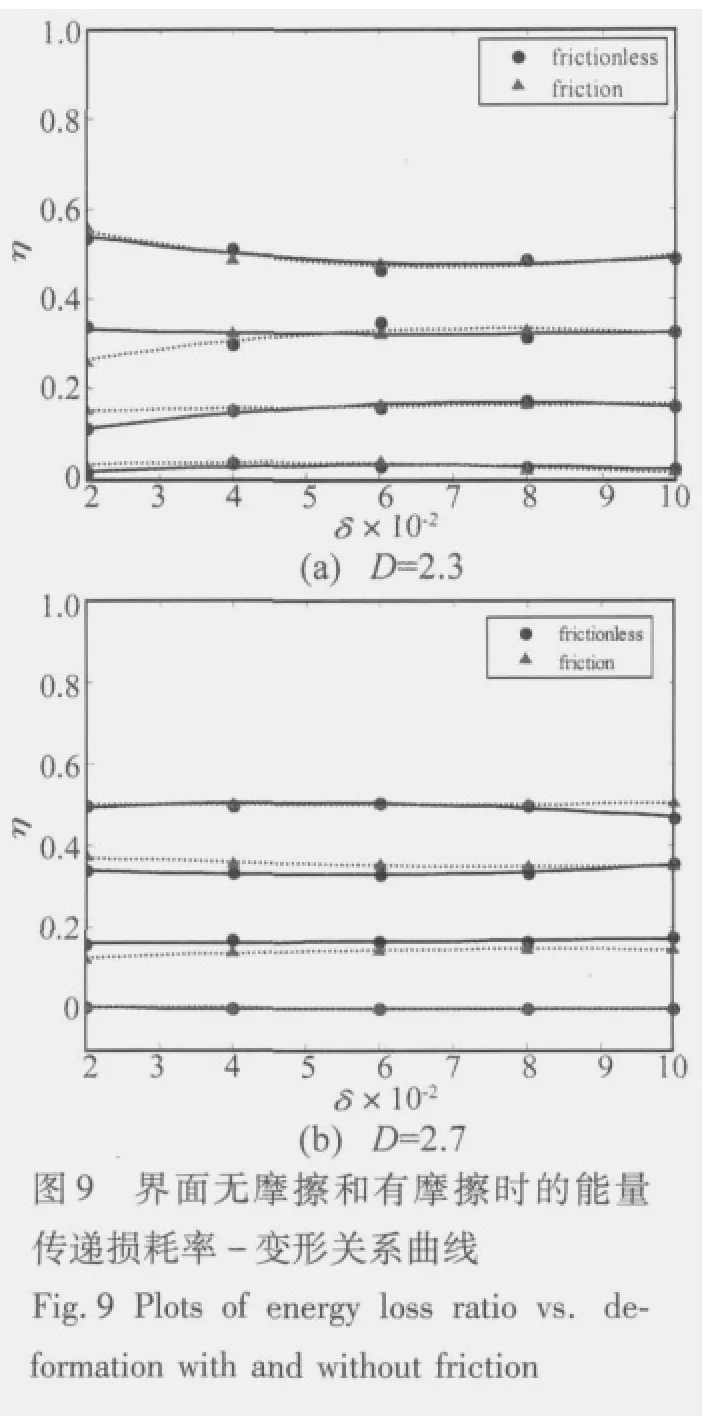
图9表示了摩擦对界面1，2，3和4的能量传递损耗率η的影响关系。对形貌Ⅰ界面(图9(a))，界面存在摩擦，变形δ较小时，能量传递损耗率η差异较大，界面1，3，4的能量传递损耗率η增大，界面2处减小;随着变形δ增大，界面摩擦对能量传递损耗率η无影响;对形貌Ⅱ界面(图9(b))，与无摩擦一致，界面存在摩擦时，不同界面的能量传递损耗率η与变形δ无关;摩擦对界面1和界面4的能量传递损耗率无影响，而使界面2的能量传递损耗率增大约3%，界面3相应减小。

上述计算结果是基于尺寸为 0.9 μm ×0.9 μm 的分形表面模型。对于其他尺寸的分形表面，由于分形函数(1)的自相似特性，在相同载荷下，不同样本长度L表征的粗糙表面具有相似的压力分布特征。因此，不同尺寸分形表面的实际接触面积大小与L2成正比，其界面接触力、接触刚度和能量损耗量的数值大小随长度L相应变化。因而，本文以尺寸为 0.9 μm ×0.9 μm分形表面进行计算研究获得的结论同样适用于其他尺寸，不同的是，接触刚度、接触力和能量损耗量的数值大小会相应发生变化。

3 结论

本文通过建立“多层粗糙金属板-刚性平面”的粗糙多界面模型，运用有限元方法，对不同界面形貌、不同塑性变形行为和界面摩擦的多层叠加模型的多界面，在加载和卸载过程中的变形、接触力以及由塑性变形和界面摩擦引起的能量损耗特性进行了研究，主要结论如下:

(1)对具有不同塑性变形行为、不同界面形貌的粗糙多界面，在加载过程中，各界面接触力随着变形呈非线性增加，接触刚度为非线性;在卸载过程中，接触力随变形呈非线性递减，接触刚度也为非线性;加载与卸载过程中，最后界面的接触刚度最大，第一界面最小。

(2)界面的加载接触力-变形关系可以用线性项、指数非线性、二次非线性和三次非线性之和表示;卸载接触力-变形关系可以用指数关系表示。

(3)加载和卸载曲线形成的滞回面积大小不同，能量损耗沿界面逐渐减小，第一接触界面最大，最后接触界面最小。

(4)粗糙度较大的界面，界面间的能量传递损耗率η与变形量δ相关，基本不受材料属性影响;对粗糙度较小的界面，界面间的能量传递损耗率η基本不受材料属性和变形量δ影响。

(5)界面摩擦将增大界面的接触力，但基本不改变各界面力-变形曲线的形状;界面摩擦对界面能量传递损耗率存在影响，即对于粗糙度较大的界面，在变形较小时影响较大;对于粗糙度较小的界面，仅对中间界面的能量传递损耗率影响较大。

［1］ Nayak P R.Random process model of rough surfaces［J］.Transactions of the ASME，Journal of Lubrication Technology，1971，93:398-407.

［2］Nayak P R.Some aspects of surface roughness measurement［J］.Wear，1973，26:165-174.

［3］ Al-Kindi G，Shirinzadeh B.An evaluation of surface roughness parameters measurement using vision-based data［J］.International Journal of Machine Tools＆ Manufacture，2007，47:697-708.

［4］ Cemal C M，Ensarioglu C，Demirayak I.Mathematical modeling of surface roughness for evaluating the effects of cutting parameters and coating material［J］. Journal of Materials Processing Technology，2009，209:102-109.

［5］邵毅敏，肖会芳.动力系统非连续单一叠加结构界面变形与能量损耗特性［J］.振动与冲击，2011，30(4):217-222.

［6］傅俊庆，荣见华，张玉萍.螺栓连接接口轴向振动能量耗散特性研究［J］.振动、测试与诊断，2005，25(3):205-209.

［7］ Ling F F.Fractals，engineering surfaces and tribology［J］.Wear，1990，136:141–56.

［8］Majumdar A， Tien C L. Fractalcharacterization and simulation of rough surfaces［J］.Wear，1990，136:313–27.

［9］Majumdar A，Bhushan B.Role of fractal geometry in roughness characterization and contact mechanics of surfaces［J］.Transactions of the ASME，Journal of Tribology，1990，112:205-216.

［10］ Sahoo P，Ghosh N.Finite element contact analysis of fractal surfaces［J］.Journal of Physics D:Applied Physics，2007，40:4245-4252.

［11］Yan W，Komvopoulos K.Contact analysis of elastic–plastic fractal surfaces［J］.Journal of Applied Physics，1998，84:3617-3624.

［12］ Wang F， KeerL M. Numericalsimulation forthree dimensional elastic-plastic contact with hardening behavior［J］.Transactions of the ASME，Journal of Tribology，2005，127:494-502.