二元翼段间隙非线性颤振的模糊控制

张军红，韩景龙

(南京航空航天大学 振动工程研究所，南京 210016)

控制面铰链的间隙非线性是飞机机翼结构中非线性的重要来源之一，对飞机的伺服气动弹性特性具有重大影响。带有控制面的二元翼段是研究这类非线性问题的基本模型。针对此类问题的非线性气动弹性响应和控制策略，已开展了许多工作。文献［1-2］对之前的研究做了综述。文献［3］采用常规的单后缘控制面以及反馈线化技术进行了主动柔性机翼结构控制研究，并得到实验验证。文献［4-5］数值仿真了包含间隙的二元翼段极限环运动并分析了其随着来流速度的变化规律。文献［6］基于状态依赖RACCATI方程推导了非线性颤振控制律。文献［7-8］将反馈线性化技术用于非线性二元翼段控制。文献［9-12］采用了非线性自适应控制技术，控制率表现出一定的稳定性和抗干扰能力。文献［13-15］采用了原用于航天轨道跟踪的参考自适应控制方法，对翼段进行控制，增大了可控速度区域。经典的控制方法一般依赖于气动弹性系统模型的准确建立。气动弹性系统是多输入多输出的复杂非线性系统，数学模型在结构上和参数上都存在着某种程度的简化，存在结构、参数、和未建模动态等诸多不确定因素。另外气动弹性系统实际工作过程中外界干扰复杂，且不可避免，所以寻找鲁棒的、适应性好的控制方法是近年来的目标之一。

本文根据模糊控制不依赖于被控对象的精确模型，对参数变化不敏感，具有很强鲁棒性的特点，提出一种模糊逻辑控制器，对包含间隙的二元机翼极限环振荡进行控制，并对其响应机理进行探讨和研究。

首先对含作动面间隙的二元翼段建立气动弹性状态方程，设计了两输入单输出模糊控制器，制定了模糊控制规则。在MATLAB/SIMULINK环境执行仿真计算，控制效果良好。当人为摄动翼段沉浮刚度10%后，控制器仍然能够迅速抑制极限环振荡，性能稳定。

1 三自由度翼段的运动微分方程

1.1 二元翼段计算模型

二元翼段模型如图1所示，为典型的三自由度翼段模型。假定翼段本身是刚性的，有三个自由度，h为沉浮运动，以向下为正，α和β分别为迎角和操纵面的偏转角，以顺时针为正。图中2b为机翼的弦长，即从机翼前缘到机翼后缘的长度，b为半弦长，ab为机翼扭转轴到翼弦中点的距离，cb为操纵面转轴到翼弦中点的距离。

系统运动方程可以表示为:

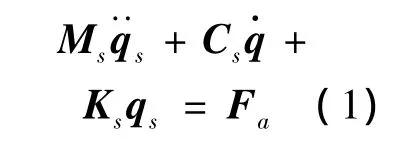
其中，Fa为气动力，系统变量qs={hα β}T。

图1 翼段结构与运动示意图Fig.1 Wing section with control panel

舵面转轴部位存在对称间隙，表示为式(4):

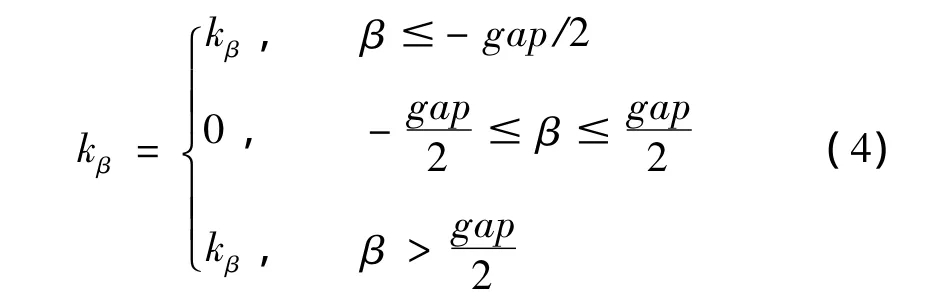
gap表示舵面间隙值。而舵面作动力矩和舵面偏转角度的关系如图2所示。

图2 扭矩和舵面转角的关系Fig.2 Restoring moment vary with β

1.2 非定常气动力和状态空间方程

文中非定常气动力采用 Theodorsen模型，由于Theodorsen［16］函数依赖于折合频率，不能直接用于时间域模拟，故用简氏近似方法，将其转化到时间域。

Theodorsen气动力表达式为:

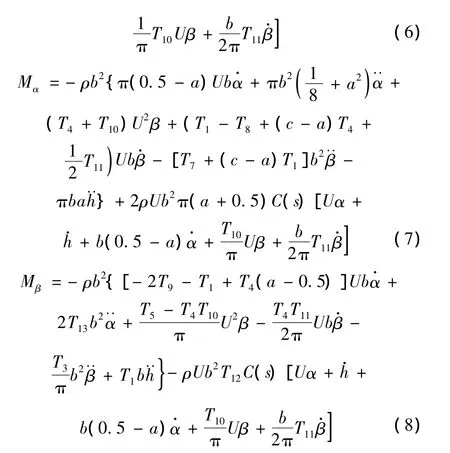
把式(6)～(8)表示的气动力，连同C(s)的简氏近似表达式带入运动方程(1)整理可得:

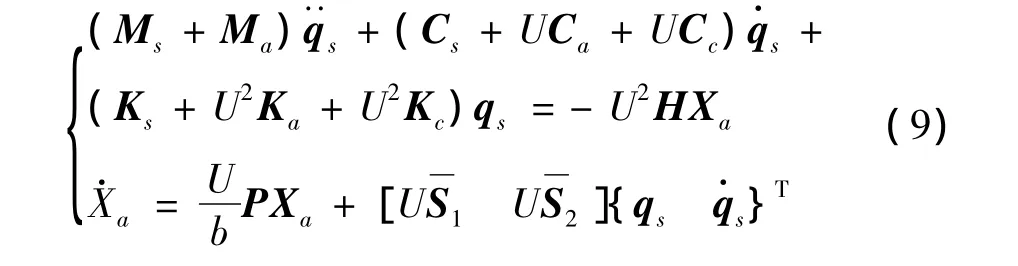
将气动弹性方程(9)写成状态空间形式为:

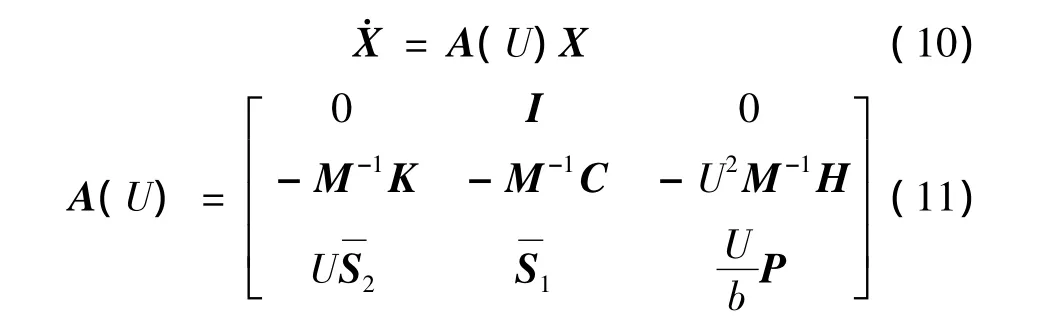
其中:U为气流速度，M=Ms+Ma;C=Cs+UCa+UCc;K=Ks+U2Ka+U2Kc;

控制面偏转指令和偏转角之间的关系如下:

包含作动的状态方程如下:

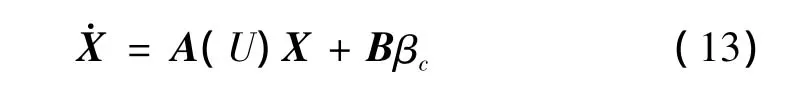
其中:

1.3 模糊神经网络控制器设计

模糊控制是以模糊集合论、模糊语言变量和模糊逻辑推理为基础的计算机数字控制方法，是目前实现智能控制的一种重要有效形式。由于飞机在飞行过程中，舵面工作状况比较复杂，结构、气动都存在非线性和不确定性，数学模型较难精确建立。而模糊控制最大的优点就是允许被控制对象没有精确的数学模型。模糊系统不依赖于系统的数学模型，具有很好的鲁棒性和适应性。

模糊控制如图3所示:

模糊控制器的输入为舵面的偏转角和角速度。模糊控制器工作流程如图4所示:

模糊控制流程

(1)论域的正则化;

(2)定义模糊集合及其隶属度函数;

(3)设计模糊控制规则集合;

(4)模糊推理方法;

图3 模糊控制Fig.3 Schematic of Fuzzy logic controller

图4 模糊控制流程Fig.4 Flow chart of Fuzzy logic controller

(5)解模糊;

(6)实时控制。

2 数值算例

结构模型采用带舵面三自由度翼段，气动力采用Theodorsen非定常气动力，考虑舵面间隙作用。模型的几何数据为b=0.5，a=0.2，c=0.6，M=18.4 kg，Sα=4.026 6 kg·m，Sβ=0.54 kg·m，Iα=1.268 4 kg·m2，Iβ=0.072 kg·m2，ωh=15.686 Hz，ξh=0.05，ωα=53.788 Hz，ωβ=20 Hz，ξα=0.05，ξβ=0.005。在 MATLAB环境中，利用SIMUINK进行时域仿真。当系统不包含间隙时，线性颤振速度为:16.01 m/s，v-g图如图5，根轨迹图如图6，v-ω图如图7所示。

当考虑舵面间隙作用，在不同的来流速度U，计算系统振动时间历程，结果表明，由于间隙的影响，当来流速度约为11.7～15.1 m/s之间时，系统响应出现极限环振动，时间历程和相位如图8～17所示。

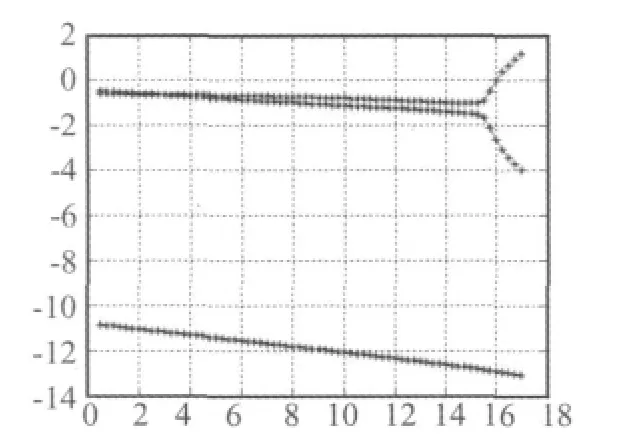
图5 v-g图Fig.5 v-g

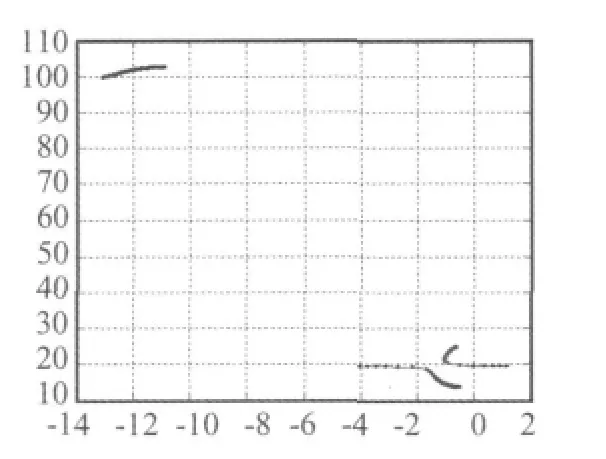
图6 根轨迹图Fig.6 Root locus

图7 v-ω图Fig.7 v- ω

图8 当U=16 m/s时，系统时间历程图Fig.8 U=16 m/s，time history of system vibration

当来流速度U大于等于15.1 m/s时，系统振动逐渐发散。由于间隙的存在，系统的颤振速度有所下降，在比较低的来流速度时发生了极限环振动，极限环振动存在于一定来流速度范围之内，并且随着来流速度的增加，极限环振幅增长，直至系统发散，所得结果与文献［4］相符。系统极限环运动，会对结构造成很大危害，本文在MATLAB/SIMULINK环境设计模糊控制器，对系统的极限环振动进行抑制。

模糊控制器以系统输出状态变量中的β和β·作为反馈，对反馈数据进行模糊化，定义模糊化集合论域为:{-6，-5，-4，-3，-2，-1，0 ，1，2，3，4，5，6}，语言变量值 NB(负大)、NM(负中)、NS(负小)、ZO(零)、正大(PB)、正中(PM)、正小(PS)，各隶属度函数都是trimf三角形隶属度函数，如图18所示。

本文中模糊控制器目标是抑制极限环振荡，使系统恢复稳定，提高颤振速度，模糊控制规则表如表1所示:

表1 模糊控制规则Tab.1 Fuzzy rule of controller

u为模糊控制器输出信号，输入给作动器。本文假定作动器是理想工作，由仿真结果可见，舵面的极限环振动被迅速抑制，如图19所示。

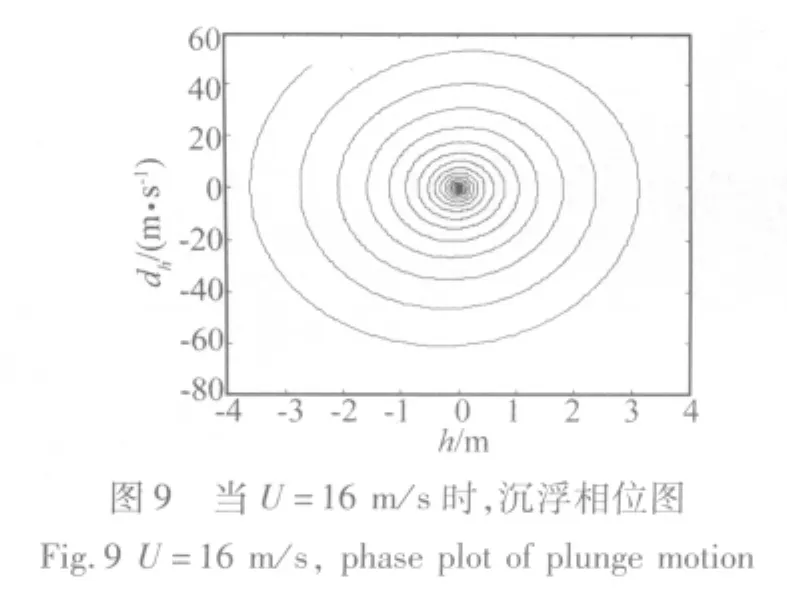
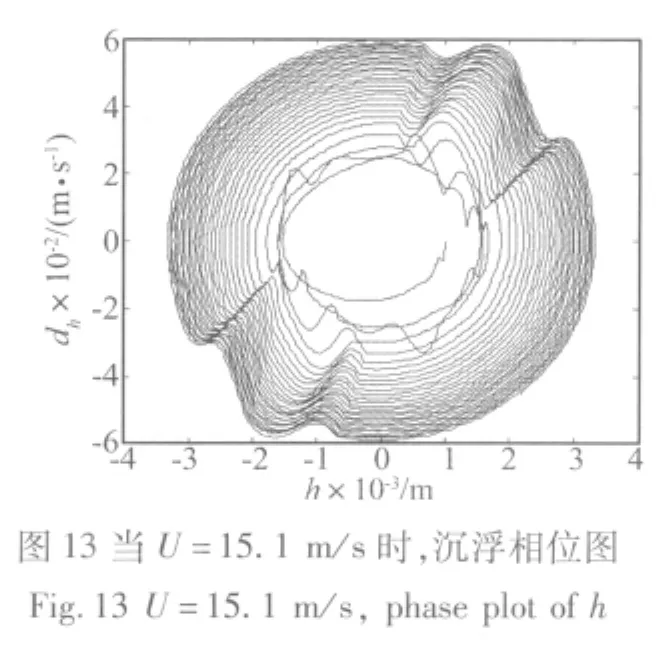
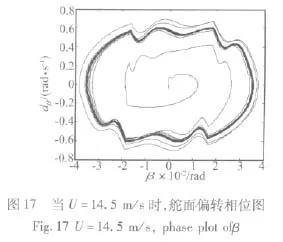
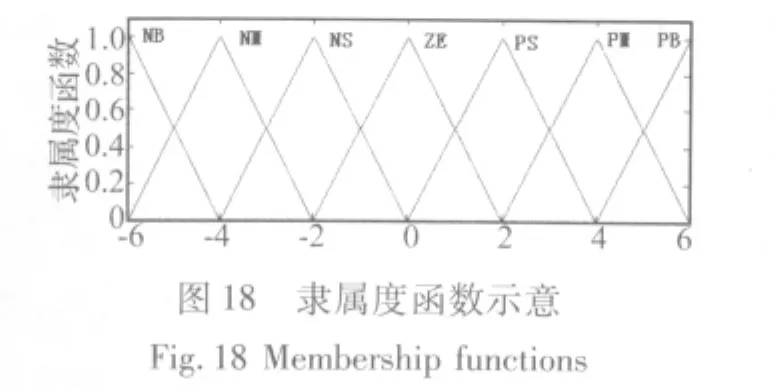
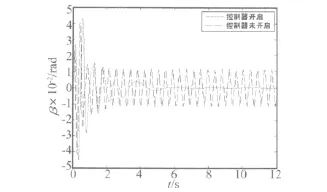
图20 舵面沉浮刚度受10%扰动时，控制效果Fig.20 Effect of controller when disturbed by 10 percent

人为对二元翼段的沉浮刚度实施10%的扰动，然后测试所设计的模糊控制器，仍然能够较好抑制LCO振动，控制效果对比图见图20所示。

3 结论

(1)仿真结果表明:由于舵面间隙的存在，系统颤振速度有所下降。在来流速度远低于线性颤振速度时，系统出现极限环振动。极限环振动存在于一定的来流速度区间，并且，随着来流速度增加，极限环幅值也增长。

(2)本文采用模糊逻辑控制器，对包含舵面间隙的二元翼段非线性气动弹性系统实施控制。结果表明，该控制器能够有效抑制间隙非线性气动弹性系统极限环振动。

(3)当人为摄动翼段俯仰刚度后，控制器仍然能够迅速产生控抑制效果，有良好的鲁棒性。该方法能够有效解决基于理想化计算模型设计的控制器在实际工作环境中控制失效或者控制效率低的问题，也能够对飞机在多工况，多任务工作，存在结构不确定、气动力不确定、或者各种非线性因素摄动的情况下实施相对稳健的控制。

［1］Mukhopadhyay V.Historical perspective on analysis and control of aeroelastic response［J］.Journal of Guidance，Control，and Dynamics，2003，26(5):673-684.

［2］任勇生，刘立厚，韩景龙，等.飞行器非线性气动弹性和颤振主动控制研究进展［J］.力学季刊，2003，24(4):534-540.

［3］Wazak M，Srinathkumar S.Flutter suppression for the active flexible wing controlsystem design and experimental validation［J］.AIAA J，1992，138-145.

［4］Conner M D，Tang D M，Dowell E H，et al.Nonlinear behaviour of a typical airfoil section with a control surface freeplay:a numerical and experimental study［J］.Journal of Fluids and Structures，1997，11:89-109.

［5］赵永辉，胡海岩.具有操纵间隙非线性二维翼段的气动弹性分析［J］.航空学报，2003，24(6):521-525.

［6］李道春，向锦武.间隙非线性气动弹性颤振控制［J］.北京:航空航天大学学报，2007，33(6):640-643.

［7］Ko J，Kurdila A J，Strganac T W.Nonlinear control of a proto typical wing section with torsional nonlinearity［J］.Journal of Guidance，Control，and Dynamics，1997，20(6):1181-1189.

［8］Ko J，Strganac T W，Kurdila A J.Stability and control of a structurally nonlinear Aeroelastic system ［J］.Journal of Guidance，Control，and Dynamics，1998，21(5):718-725.

［9］Behal A，Marzocca P，Rao V M.Nonlinear adaptive control of an aeroelastic two-dimensional lifting surface［J］.Journal of Guidance，Control，and Dynamics，2006，29(2):382-390.

［10］ Xing W，Singh S N.Adaptive output feedback control of a nonlinear aeroelastic stucture［J］.Journal of Guidance，Control，and Dynamics，2000，23(6):1109-1116.

［11］ Kanellakopoulos I，Kokotovic P V，Morse A S.Systematic design of adaptive controllers for feedback linearizable system［J］. IEEE Transactionson AutomaticControl，1991，36(11):1241-1253.

［12］ Zhang R，Singh S N.Adaptive output feedback control of an aeroelastic system with unstructured uncertainty［J］.Journal of Guidance，Control，and Dynam-ics，2001，24(3):503-509.

［13］ Ko J，Strganac T W，Junkins J L，et al.Structured model reference adaptive control for a wing section with structural nonlinearity［J］.Journal of Vibration and Control，2002，8(5):553-573.

［14］ Strganac T W，Ko J，Thompson D E，et al.Investigations of limit cycle oscillations in aeroelastic systems［R］.CEAS/AIAA/ICASE/NASA Langley，International Forum on Aeroelasticity，Williamsburg，Virginia，1999.

［15］ Akella M R. Structured adaptive controltheory and applications to trajectory tracking in aerospace systems［D］.Department of Aerospace Engineering， Texas A＆M Unibversity，1998.

［16］ Theodorsen T.General theory of aerodynamic instability and the mechanism of flutter［R］.NACA Report No.496，1935.