基于过程突变理论的监测数据动态检验模型研究

刘洪海

(重庆市勘测院，重庆 400020)

1 引言

监测数据的误差一般可分为三类:粗差、偶然误差和系统误差。在相同的观测条件下作一系列观测，若误差的大小及符号都表现出偶然性，这类误差称为偶然误差或随机误差，一般通过一定的数据处理比如最小二乘法等评定监测系统的精度;同样，在相同的观测条件下做一系列观测，若误差的大小及符号表现出系统性，或按一定的规律变化，那么这类误差称为系统误差;粗差是由于测量人员的粗心大意、仪器精度达不到要求或突发性故障等原因而产生的超过3倍中误差的异常数据，它严重影响了监测结果的正确性，绝不能采用，以保证不影响对建筑物安全形态的正确判断。

2 监测数据的预处理

操作人员失误、环境条件与仪器等因素的影响，监测数据中各种误差在所难免，如果不对含有各种误差的监测数据进行预处理，有效地对粗差进行探测、识别及控制，将会对参数的估计结果产生严重影响，从而导致对建筑物的形态作出错误的判断［1］。

监测数据的预处理可以有效剔除粗差，改进数据的质量，从而有助于提高其后处理过程的精度和数据使用性能。

3 目前常用的几种粗差检验方法

目前常用的粗差检验方法在数据采集阶段一般采用比较粗略的方法，如几何条件检核法、逻辑检验法、监控指标控制法等;在数据处理阶段则主要有包络域检验法、时空评判准则检验法、模型检验法、统计检验法等;在粗差成因分析阶段则主要有模拟数据分析法、有限元分析法、关联分析检验法等，这些方法各有千秋，但是大量研究［2～4］表明，使用单一方法对监测数据中粗差的剔除效果总是不尽如人意。

4 过程突变模型的建立

设{y(t)，t∈T}为给定的一组时间T上的变形监测数据，该组数据的平均值为 μ(t)=E［y(t)］，当{μ(t)，t∈T}在不同的分段上具有连续性且平方可积时，μ(t)=E［y(t)］就具备了用L2空间上选定的基函数{θ(t)，i=1，2，3…}组的线性组合逼近的充分必要条件［5］。建筑物变形监测数据正常观测值可采用如下线性模型进行拟合:

其中:ε(t)为各种来源误差的综合影响值;

{αi，i=1，2，3，…s}为特征系数。

如果该组变形监测数据中存在粗差，与式(1)进行比对，则含粗差的变形监测数据的数学模型为:

其中:τ为粗差产生的初始时间;λτ为初始粗差幅;

函数φ用下式确定:

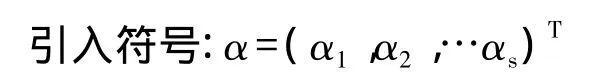
正常观测值线性模型拟合系数的最小二乘法估计递推关系式为

分别为{θ(t)，i=1，2，3…}生成的向量和矩阵

当变形监测数据正常观测值线性模型与实际观测值相吻合时，模型系数的最小方差线性无偏估计即为^αn。因递推最小二乘法存在对粗差容错能力弱的缺陷，在实际变形监测数据存在较大的粗差的情形下，若按正常观测值线性模型拟合系数的最小二乘估计递推关系式来求算模型拟合系数，结论不具备可靠性。

为提高最小二乘法估计递推关系式对粗差的容错率，本文提出的改进了的最小二乘法估计递推关系式为:

其中:C为门限常数。假设置信水平取95%，置信带宽取±1.96 s，其中 s是标准差的残留量，则C=1.96 s。

5 变形监测数据中粗差的检测

根据含粗差的变形监测数据的数学模型、可以以在线的方式推求改进了的最小二乘法估计递推关系式和定义于R上的为最小方差有界奇函数ω(ξ)，则变形监测数据的一步容错估计［6］。

当置信区间为{In+1，n=1，23…}序列，变形监测数据观测值的在线检验方法可以如下构建:

如果y(tn+1)∈In+1，即可判断y(tn+1)为非正常，且此时置信度大约为 (1－△)×100%，进而可以对该观测点的相关检测点进行检验，倘若该相关检测点也与该点存在类似的非正常，则可以判断该观测点为可疑测点，并且立刻进行实地考察判断这个建筑的结构是否存在整体变形;反之，如果对该观测点的相关检测点进行检验的结果表明相关检测点为正常，则可以判断该观测点的问题仅仅是变形监测数据值含有粗差。

6 应用实例

为验证上述基于过程突变理论的监测数据动态检验模型的检验效果，选用2007年1月～2011年4月对重庆市某大型标志性建筑物顶部测点的位移监测资料。该项目平均每月观测2次，共计获得100个检测值 yi(1，2，…，100)=Li。

本次研究中分别在y10、y20、y30…y100等10个变形监测数据观测值上同时加 5 mm的粗差，并分别用含粗差的变形监测数据观测值和不含粗差的变形监测数据观测值用上述基于过程突变理论的监测数据动态检验的模型进行检验，计算步骤如下:①输入实测值。②据式(4)计算y˜(t)。③据式(7)计算pn+1、据式(8)计算、据式(9)计算。④据式(12)计算。⑤据式(13)计算 ε˜n+1。⑥据式(14)计算In+1，并据此判断是否越界，如果否认，则录入计算机，如果判断数据越界，则对该变形监测数据观测点的相关检测点进行检验。⑦如果其相关变形监测数据检测点也存在大致相同的异常，则将该变形监测数据测点确定为可疑测点。⑧进行实地考察判断这个建筑的结构是否存在整体变形，否认则认为仅是该变形监测数据存在粗差。⑩进行变形监测数据的一步容错估计。

7 结果与结论

本研究中，计算结果表明，过程分别在y10、y20、y30…y100等共10个变形监测数据观测值上发生了突变，与事先设置的模拟粗差相吻合。

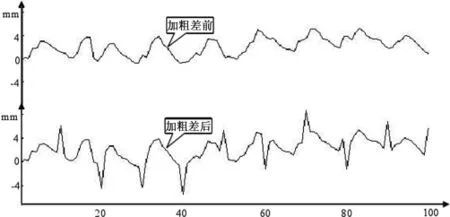
图1 人为添加粗差前后的测值过程线

图2 变形监测数据的一步容错估计残差

本模型计算过程简单、计算量小，尤其在实时形变监测系统连续实时动态显示监测数据、数据量巨大的情形下结合关联分析检验法对建筑物变形监测实测数据进行异常值判断、突变值标识以及趋势性变化识别效果显著［8］，从而提高了自动化监测系统的实用性，为得出建筑物的整体性状结论提供辅助决策，有效地确保了建筑物的安全。

［1］徐天河，贺凯飞．移动开窗检验法及其在GOCE数据粗差探测中的应用［J］．测绘学报，2009，10，38(5):391 ～393．

［2］Pizhong Qiao，Kan Lu，Wahyu Lestari，Jialai Wang．Curvature mode shape－based damage detection in composite laminated plates［J］．Journal of composite structures，2007，80:409～428．

［3］张勇，静行，袁海庆．基于模态曲率变化率指标的结构损伤识别［J］．华中科技大学学报(城市科学版)，2010，27(2):82～86．

［4］刘涛，李爱群，赵大亮等．改进模态应变能法在混凝土组合箱梁桥损伤诊断中的应用［J］．工程力学，2008，25(6):44～50．

［5］管德清，黄燕．基于应变模态小波变换的框架结构损伤识别研究［J］．计算力学学报，2010，27(2):325～329．

［6］M．Mehrjoo，N．Khaji，H．Moharrami，A．Bahreinineja，Damage detection of truss bridge joints using Artificial Neural Networks［J］．Expert Systems with Applications，2008，35:1122～1131．

［7］Xiaomo Jiang and Sankaran Mahadevan．Bayesian wavelet methodology for structural damage detection［J］．Struct．Control Health Monit．2008，15:974 ～991．

［8］Wei Fan，Pizhong Qiao．A 2－D continuous wavelet transform of mode shape data for damage detection of plate structures［J］．International Journal of Solids and Structures，2009，46:4379～4395．