基于构建Delaunay三角网和平面拟合法组合的GPS高程转换

王新 ，张绍良

(1.中国矿业大学环境与测绘学院，江苏徐州 221008;2.江苏省资源环境信息工程重点实验室，江苏徐州 221008)

1 引言

与常规水准测量相比，GPS水准具有费用低、效率高、观测时间短、操作方便、全天候等特点，因此在为研究地表形变的变化机理提供动态监测数据有着独特的优势。但GPS测量是在WGS－84坐标系中进行的，所提供的高程为相对于WGS－84椭球的大地高H，而我国在工程实际应用中使用的是正常高Hr。为此，必须将GPS大地高H转换成正常高Hr，二者之间的差值称为高程异常 ζi［1～2］。

目前实现GPS大地高与正常高之间的拟合方法有很多，包括:加权均值法、多项式曲线拟合、多项式曲面拟合、多面函数曲面拟合、线性移动拟合法、神经网络法、支持向量基回归(SVM)模型等［3～7］。其中以多项式曲面拟合中的平面拟合法最为简单，容易编程实现，但是单一的平面拟合法却难以满足较大范围和地形变化比较大的地区，文献［8］指出高程异常由中长波段的趋势项(地球重力场和重力异常)和短波项(地形起伏引起的高程异常)组成，而在 20 km～200 km内中长波段的趋势项变化趋势和大地水准面变化趋势基本相同且变化趋势平缓，即只与坐标有关，可用一般拟合函数进行拟合。而短波项与地形信息相关，变化比较复杂，大区域内不能拟合。基于此种原因，提出构建Delaunay三角网和平面拟合法的组合模型，将联测点构建成Delaunay三角网，使整个区域分成若干三角形小区域，然后插入待拟合点进行Delaunay重构，选择与待拟合点相关联的联测点，并且使用逐点剔除法优化这些关联点，选择最佳拟合组合进行平面拟合函数的求取［9］，进而得出待拟合点的高程异常。本文利用MATLAB编程建立GPS高程拟合系统，通过实例验证得出:该方法可以提高拟合精度，并且能为GPS水准联测点的分布密度和位置选取提供建议。

2 算法模型和程序实现流程

2.1 算法模型

(1)平面拟合模型

多项式曲面拟合的一般公式为［10］:

其中 ζi(xi，yi)为点(xi，yi)的高程异常，ai待求参数，当参数只有3个时，即为平面拟合。

平面拟合法数学表达式为:

式中xi和yi为联测点的平面坐标，ζi为相应的高程异常，a0、a1、a2为待定系数，因此为求出待定系数的值必须要有3个或3个以上的联测点。

(2)Delaunay三角网算法

生成Delaunay三角网的算法主要分为三类:分治算法;逐点插入法，三角网生长法［10］。本文采用分治算法，该算法首先由 Shamos和 Hoey提出［11］，Lewis和Robinson将该算法首先应用于Delaunay三角网。

分治算法的具体步骤为:首先把所有的离散点进行以X坐标为主Y坐标为辅升序排序，将点集平均分成数据点个数相等的两个子集，在每个子集里再次分成数量相等的子集，直至每个局部区域里的数据点数满足所给的阀值。在每个子区域里构建凸包生成Delaunay三角网，寻找相邻凸包之间两凸包的顶支撑线和底支撑线，对两线与凸包边界围成的多边形区域三角网化，并用局部优化准则对其进行优化。

(3)区域GPS水准优化模型

若通过重构Delaunay三角形得到的关联点为n个，本文使用平面拟合模型，即选取3个或3个以上的点拟合即可。使用逐点剔除法从n个关联点中逐点剔除对拟合精度贡献最小的点，最后剩下的3个关联点就是GPS水准拟合计算的最优拟合方案。

从n个点中剔除一点，共有n种剔除方案，选择其中使得拟合精度最高的一个方案作为n－1个点时的最佳拟合方案，这样就剔除了一个点。以此类推，直到剩下3个点，即为最优的GPS水准点。这样该算法总共需要计算n+(n+1)+…+(3+1)中方案。然后比较3～n点拟合方案中拟合精度最高的作为最终拟合方案，所选中的点为最佳拟合点，相应分布为最佳分布［12］。

2.2 程序实现流程

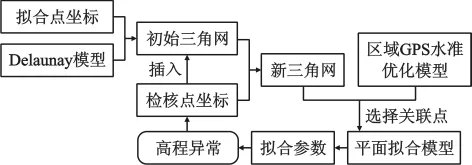
图1 程序实现流程图

3 实例计算与分析

某GPS控制网有37个GPS控制点(图2)，联测四等水准［13］。将 2、20、31、53、87、96、116、143、157、187、190、225、242、243、255、265、291 号点作为初始构网拟合点，其余点为检核点。当插入检核点(以50号点为例)后构成新的三角网。从图3可看到与检核点构成三角网的拟合点，对这些拟合点进行优化，选出最优的拟合组合进行拟合参数的求取。

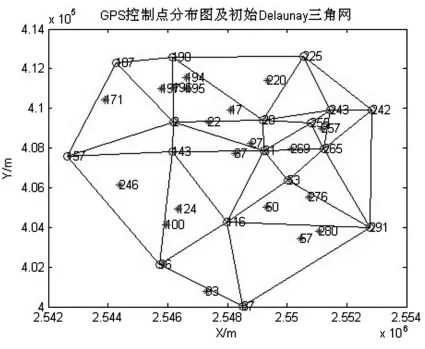
图2 拟合点分布图及初始Delaunay三角网

图3 重构后的Delaunay三角网

当插入高程异常构成三维Delaunay三角网后(图4)，可以清楚地看到高程异常面变化非常不规则，常规的曲面函数拟合势必造成较大的误差，因此使用Delaunay三角剖分，将大区域按照地形变化分成多个三角形小区域可以更为精确地描述出高程异常的变化趋势，提高拟合精度。因此，地形变化较大地区，为提高拟合精度必须增加联测点的数量和制定合理的联合点分布位置。

图4 三维Delaunay三角网

为进一步提高拟合精度，使用逐点剔除法选择最佳拟合方案，使拟合结果最优。计算得出拟合中误差为±1.9 cm，拟合误差最大的两个点分别为246、93，拟合误差分别为 4.8 cm、4.6 cm。从图5和原数据分析具体原因为:246、93两点所处位置地形变化较大(相关联拟合点高程异常最大差距分别为21 cm、27 cm)，且所测联测点比较稀疏(只有3个关联点)，无法体现出地形变化，具体数据如表1所示。

几种拟合方法所得结果如表2，具体残差比较如图5所示。从计算结果可以看到，本文方法能提高拟合精度。

通过表1和图5可以看出，各种拟合算法的误差走向相似，最大拟合误差均出现在93、246两点，且本文方法在各点的拟合精度均高于其他方法。

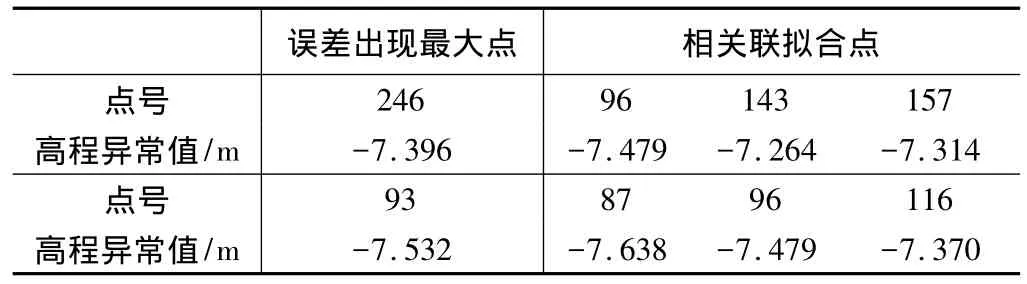
误差最大点及相关联拟合点数据表 表1

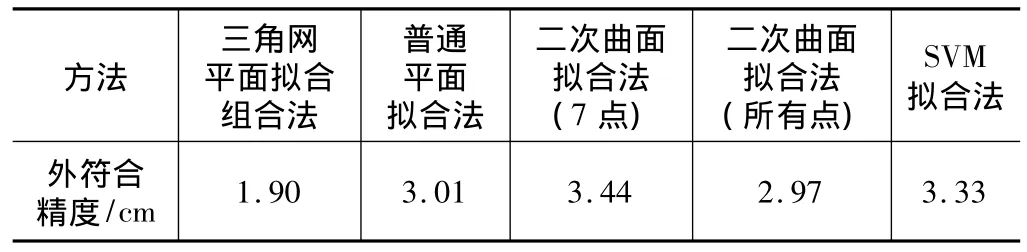
四种方法计算结果比较表 表2

图5 残差比较图

4 结论

(1)利用构建Delaunay三角网和平面拟合组合法进行GPS水准拟合时，是将大区域以地形变化划分为多个三角形小区域，并以待拟合点内插重构三角形为基准进行拟合，避免了大区域单一拟合函数造成的误差。

(2)利用构建Delaunay三角网和平面拟合组合法进行GPS高程转换时，其精度与测区的似大地水准面的复杂程度、水准点的密度和分布有关，足够的密度和合理的分布，是保证转换精度的必要条件［14］。

(3)使用GPS水准优化法选择关联拟合点的最优组合能剔除可能造成拟合值发生突变的拟合点，提高拟合精度。

(4)通过实例计算表明，该方法容易编程实现，可进行大批量GPS水准拟合，并且通过对比构建Delaunay三角网和平面拟合组合法有较高精度。

［1］ 李征航，黄劲松．GPS测量与数据处理［M］．武汉:武汉大学出版社，2005．

［2］宁津生，刘经南，陈俊勇等．现代大地测量理论与技术［M］．武汉:武汉大学出版社，2006．

［3］张小红，程世来，许晓东．基于Kriging统计的GPS高程拟合方法研究［J］．大地测量与地球动力学，2007(2):47～51．

［4］杨明清，朱达成，陈现春．用神经网络方法转换GPS高程［J］．测绘学报，1999(4):301～307．

［5］王继刚，胡永辉，孔令杰．基于最小二乘支持向量机的区域GPS高程转换组合［J］．大地测量与地球动力学，2009(5):99～102．

［6］高伟，徐绍铨．GPS高程分区拟合转换正常高的研究［J］．武汉大学学报(信息科学版)，2004(10):908～911．

［7］ 丛康林，岳建平．基于SVR的GPS高程拟合模型研究［J］．测绘通报，2011(2):8～11．

［8］王旭，刘文生．GPS高程拟合方法的研究［J］．测绘科学，2010(35):28～30．

［9］沈云中，高达凯．GPS水准点优化选择法［M］．两岸重力及水准面研讨会，台北，2003:131～135．

［10］刘万选，刘加生．两种常用的GPS高程拟合模型拟合精度研究［J］．测绘与空间地理信息，2009，32(3):147～150，156．

［11］Shamos M I．and Hoey D．Closest－point Problems，In:Proceedings of the 16th Annual Symposium on the Foundations of Computer Science［C］．1975，151 ～162．

［12］赵超英，刘雷．GPS水准拟合优化法探讨［J］．工程勘测，2006(2):64～67．

［13］金雪汉，尹长林．GPS高程转换中的函数模型逼近研究［J］．长沙电力学院学报(自然科学版)，2005(2):75～77．

［14］陈鹏，陈正阳．广义延拓法在 GPS高程转换中的应用［J］．大地测量与地球动力学，2010，30(2):125～128．