航天器碰撞概率计算方法研究进展

杨维维 赵勇 陈小前 王振国

（国防科技大学航天与材料工程学院，长沙 410073）

1 引言

随着人类航天事业的快速发展，近地空间在轨运行航天器数量急剧攀升，大大提高了轨道飞行器碰撞的可能性。2009年2月10日美国“铱－33”卫星与已报废多年的俄罗斯“宇宙－2251”卫星相撞，这是首次在轨卫星相撞事件，使航天器在轨安全问题成为研究焦点。

目前国内外对航天器碰撞风险评估最常用的方法，是最小距离法和碰撞概率法。最小距离法相对简单，但虚警率高，易导致频繁轨道机动从而降低飞行效率，且不能提供量化的评估指标，不便于制定最优碰撞规避机动策略［1］。为了提高决策准确度并减少机动次数，美国航天飞机在2001年采用了基于碰撞概率法的防撞规避机动［2］。碰撞概率法综合考虑了航天器与目标的相遇几何关系和状态误差协方差，能更有效地进行碰撞风险评估。因此，近年来基于碰撞概率的空间目标碰撞预警和规避机动研究受到广泛关注。

本文首先描述了航天器相遇问题，介绍了航天器线性及非线性相对运动条件下几种典型碰撞概率计算方法并归纳了各方法的特点及适用性；同时，总结了某时刻的瞬时碰撞概率及最大瞬时碰撞概率的计算方法；最后分析了现阶段研究存在的问题及未来的研究方向。

2 航天器相遇问题描述

考虑到空间环境及状态测量的不确定性，一般采用椭球体描述质心位置测量误差分布。对于近圆轨道航天器，其速度方向基本与椭球最大主轴一致。除误差椭球外，航天器有自身物理安全区域。目前研究大多采用球体作为航天器刚体包络体，忽略航天器姿态对相遇模型的影响，球半径也称为等效半径。对于形状明显不规则的航天器，如航天飞机、国际空间站等，则需要考虑非球形包络体，从而提高碰撞概率计算精度。

通常将可操作的航天器称为主对象（或主星），对应的次对象（或次星）可为轨道碎片或是在轨工作或报废的航天器。一般将两航天器的位置误差方差nσ联合起来形成联合误差椭球，将刚体包络体联合起来形成联合包络体，中心位于主星质心。相遇域指描述相遇模型的空间区域，Chan通过数值积分，得出相对运动可近似为直线的相遇域范围［3］。图1给出了包络体为球形的航天器相遇示意。

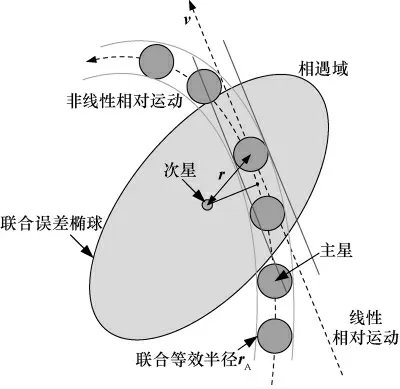
图1 航天器相遇示意Fig.1 Description of spacecraft encounters

由图1可知，当相对位置r与相对速度矢量v 垂直时，两目标相距距离最小，即两者处于垂直于v 的平面上，定义该平面为相遇平面，并以该平面为基准面定义相遇坐标系［4］；碰撞概率定义为两个位置预报有误差的空间物体发生碰撞的概率［5］，即两物体距离小于联合等效半径的概率。设位置误差联合协方差为C，相遇域内高斯概率密度函数（Probability Density Function，PDF）定义为

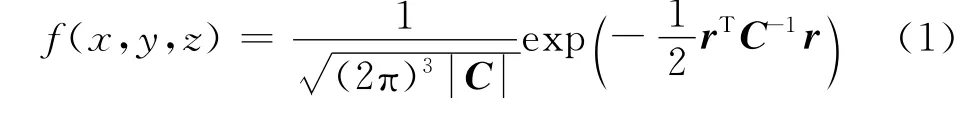
碰撞概率为

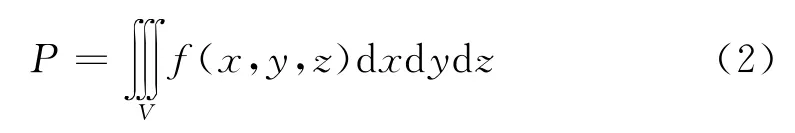
式中 V为等效半径rA的包络体在相遇域内运动所扫过的体积。

由定义可知，碰撞概率是指整个相遇过程的总碰撞概率。对于线性相对运动，联合球体扫过的体积为无限长圆柱体，可将三维积分转化为二维面积积分。但对于非线性相对运动，由于相对速度大小和方向均随时间变化，定义的坐标系也随之改变，误差椭球的形状、大小及方向都为时变，三维积分计算较为复杂。

对于某些特殊应用，如构形重构等，更关注机动过程中某时刻的碰撞概率，即瞬时碰撞概率。这时积分体积V 即为联合包络体。若次星的位置误差协方差未知，可计算瞬时碰撞概率最大可能值，为预警最坏情况提供依据。

3 线性相对运动碰撞概率计算

早期研究的航天器和空间碎片的碰撞问题主要针对线性相对运动，其计算方法比较成熟。常用线性相对运动碰撞概率计算的基本假设为：

1）相遇时间短（通常为几秒），相对运动可以简化为线性模型；

2）相对速度矢量在相遇期间保持不变，积分体近似为无限长圆柱体；

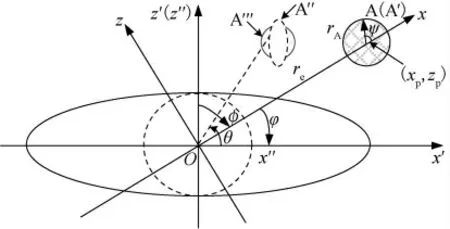
图2 航天器线性相对运动相遇平面示意Fig.2 Encounter plane of spacecraft with linear relative motion

3）两空间目标位置误差PDF在相遇期间保持不变。

通常联合协方差C 包含非对角项ρxz，文献［6］分析了协方差相关性对碰撞概率的影响。为简化处理，作坐标系旋转变换使得协方差阵在新坐标系Ox′z′中为对角矩阵C′。对非各向同性情况，不失一般性，设σx′＞σz′，再次进行坐标转换，使新坐标系中C″对角项相等（即文献［4］提出的空间压缩），若联合包络体为球体，则此时积分圆截面A′变换为椭圆截面A″。该坐标变换不可避免地带来原有几何关系的失真，如图2所示。

典型的线性相对运动碰撞概率计算方法有：Foster等推导的极坐标形式的二维数值积分法（NASA 模型）；Patera的沿截面轮廓一维积分法；Alfano沿轴向的一维积分法以及Chan的近似解析表达计算法［7－11］。

（1）NASA 模 型［7］

模型计算公式如下：

式中 φ＝π／2－φ，φ为坐标轴旋转角，如图2所示。

（2）Patera模型［8－9］

经过两次坐标转换后，积分降为关于椭圆联合包络体轮廓的线积分。

式中 θ为原点到椭圆轮廓上点的连线与坐标轴的夹角。碰撞概率沿椭圆轮廓逆时针方向进行数值积分。

（3）Alfano模型［10］

将二维积分在相遇面（x′，z′）上降为一维积分，模型计算公式如下：

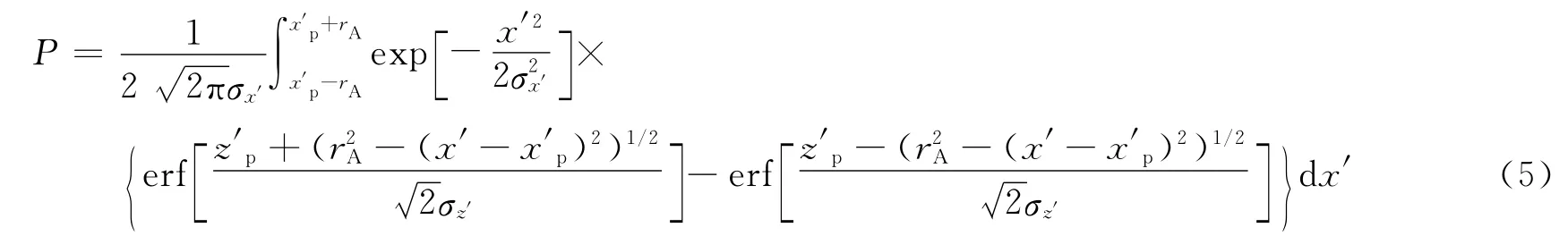
式中 erf［·］为高斯误差函数。

（4）Chan模型［11］

假设rA／σ为小量（rA／σ≤0.1）且0≤re／σ≤100，采用等价截面面积法将椭圆截面A″用圆A‴代替，从而将二维积分简化为一维Rician PDF 积分，推导出无穷级数形式表达的解析解。其零阶近似计算公式为：

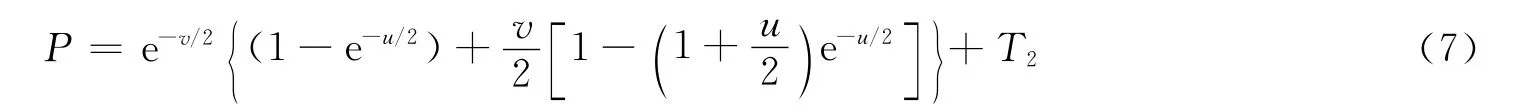
对于圆碰撞截面，文献［3，10］给出了以上计算方法的仿真比较，4种模型得出的碰撞概率精度均达10－5。NASA 模型是严格基于圆横截面推导的精确解，数值积分精度与步长相关，但计算量较大；Patera模型未做任何假设，其结果与NASA 模型的误差最小；Alfano模型中由于误差函数需通过数值计算，其结果包含计算误差函数的截断误差；Chan模型采用解析表达近似计算，其优点是计算速度快且解析表达有利于进行参数影响分析。模型计算误差除截断误差外，还包含截面近似转换带来的误差，精度不及其他3种方法，但仿真表明误差仍在可接受范围内。其缺点是模型适用条件较为严格，对于未来导航精度较高的航天器不适用。

通常航天器包含多种形状部件（如球体、圆柱、圆锥及长方体等）。在相遇面上，这些部件往往因相互遮挡使得包络体截面形状不规则。NASA 模型只能用于圆截面，不能推广到复杂截面。Patera和Alfano模型可扩展应用到复杂包络截面航天器，如绳系卫星，但积分计算较繁琐［12］。由于采用等价截面面积法，Chan模型可用于近似计算任意复杂结构航天器的碰撞概率，如国际空间站，其计算精度与截面圆近似程度相关［3］。

除上述方法外，文献［4］推导了圆轨道航天器的相遇几何描述参量（过交线高度差、时间差及轨道面夹角）和RSW 坐标系误差协方差表示的碰撞概率解析表达，本质上与Chan模型一致。

4 非线性相对运动碰撞概率

对于非线性相对运动，积分体积不再是无限长圆柱体，上节描述的计算方法均不再适用。非线性相对运动碰撞概率计算具有如下特点［13］：

1）与线性相对运动碰撞概率计算方法的输入参数相同；

2）整个相遇过程中位置误差PDF可随时间变化，即误差椭球的形状、大小及方向可变；

3）空间目标在相遇面上的截面可随时间变化。

非线性相对运动碰撞概率计算方法的难点在于积分体积的描述及其计算的复杂性。即使包络体在实际空间中静止，但只要误差椭球发生旋转变化，则包络体中心在新坐标系下将沿圆弧移动。积分体积V 一般呈现带有曲线轴且截面积变化的管状，如圆环、椭圆环甚至是卷饼状［3］。当相对运动轨迹具有高度非线性时，相对速度可能反向导致积分体自相交，这时计算更为复杂。因此，非线性相对运动碰撞概率计算很难获得精确解，大多只能采用近似处理。

目前典型的非线性运动碰撞概率计算方法有：Patera的柱坐标系描述的对称空间积分形式，Alfano的笛卡尔坐标系分段积分模型以及Chan提出的近似解析模型［3，12－13，15－16］。

（1）Patera模型［12－13］

该模型采用对称空间概念，经坐标变换使C 对称化，然后通过正交变换至相遇系。将积分体积沿相对速度方向按时间分段计算，假设各时间步长内PDF、rA以及v为常数，定义参数z／σ计算碰撞概率速率，通过时间积分计算总的碰撞概率，值得注意的是，联合包络体扫过的体积不能重叠。该方法的精度主要取决于假设条件速度方向不变的满足程度。

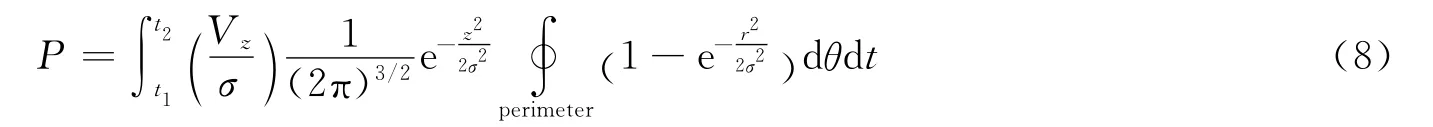
通过与蒙特卡洛仿真进行比较，建议采用3σ相遇椭球体；但当出现相对速度反向时，3σ法不适用［14］。

（2）Alfano模型［15］

该模型将积分体积沿相对速度方向分为多段，各段对应的概率求和得出总碰撞概率。分段步长需充分小以满足线性相对运动假设，然后选择任意线性运动的模型计算二维碰撞概率。沿相对速度方向的一维概率通过两端点的马氏距离（Mi，Mf）计算。各段碰撞概率为一维及两维的概率乘积。对于非线性运动，积分段之间存在间隙和重叠，若相对运动轨迹向协方差椭球中心弯曲，则重叠部分发生在较大概率密度区域，间隙发生在较小概率密度区域。尽管重叠与间隙的体积几乎相等，但求和后导致总碰撞概率偏大。该模型的误差主要取决于运动轨迹相对误差椭球中心的弯曲度。

对于典型的椭圆环积分，将其分为多个小圆柱，沿相对速度方向z轴的概率为

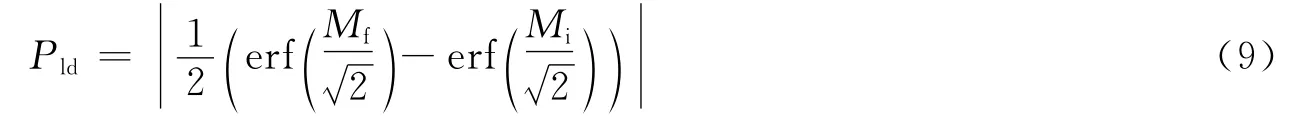
为平衡计算速度和数值精度，文献［15］通过试差法得出：一般最大时间步长设置为100s，圆柱体之间连接的最大允许角度为1°。

（3）Chan模型［3，16］

假设条件：1）相对运动共面无漂移，满足C－W 方程；2）各向同性，即三轴位置误差方差均为σ且时不变；3）联合球体半径时不变。采用数值估算面积及等效面积法将积分体积转换为圆环，二维环面积分采用一阶近似解析解，可得近似碰撞概率为

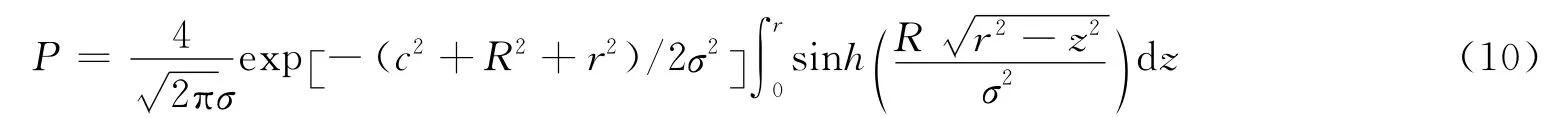
式中 c为相对运动椭圆中心沿轴向偏移常量。对于圆相对运动轨迹，式（10）为精确解。当Rr／σ2＜0.1时，有近似解析解：

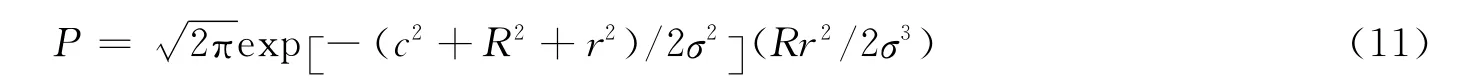
该模型的主要误差来自采用等效面积法对积分体积的影响及一阶近似的截断误差。当A／σ＞1.5时，将椭圆环分成多个区域采用线性模型的近似解析解计算各区域的碰撞概率。

综上所述，Patera与Alfano模型均沿速度方向分割积分体积，将三维非线性碰撞概率转化为二维线性概率与一维（相对速度方向）概率的乘积。分段步长足够小以满足线性相对运动的基本假设条件。Petera模型根据时间步长分段，Alfano模型根据相对速度方向距离步长分段。而Chan模型基于C－W 方程推导的椭圆相对轨迹，沿垂直于运动平面方向分割体积，利用近似解析解计算二维环面积分。展开式（9）可得：

由式（8）可知，Patera与Alfano模型在本质上是等价的，但Patera模型采用对称空间可能会引起角度失真、物理意义不明确（比如坐标旋转变换导致相对速度不再是轨迹切线）等问题。当时间积分步长足够小时，二维概率计算方法是Alfano与Patera模型差异的主要原因。Chan模型将三维积分简化为一维积分，计算速度较快，但受假设条件的限制。当Rr／σ2足够小时，可利用解析表达式（11）求导得出最大碰撞概率对应的几何构形，从而指导编队航天器相对构型的安全设计。文献［15］对有精确解的积分体积为圆环的碰撞概率进行了仿真比较，得出3种模型的误差为2%左右。

除上述模型外，文献［15］还提出了在Mahalanobis空间创建三维像素网格的方法，但该方法不易理解且计算较为复杂。文献［17］提出的计算方法与Alfano模型相似，考虑了分段小圆柱体之间的间隙与重叠区域的计算从而提高精度，但同时也大大增加了计算量。

5 瞬时碰撞概率

对于非线性相对运动相遇模型，计算总碰撞概率并不能有效进行碰撞预警，针对某些应用，如长期近距离相对飞行任务，更关注最大瞬时碰撞概率。瞬时碰撞概率定义为某时刻次星位置落在总包络体内的概率［5］。瞬时碰撞概率计算方法主要有直接法、近似分布法及等效体积法。仿真结果表明近似分布法易产生虚预警，对小碰撞概率事件不适用［3］。

最大瞬时碰撞概率定义为相对运动过程中瞬时碰撞概率的最大值，也可广义定义为误差协方差未知情况下，某时刻瞬时碰撞概率最大可能值。它是描述两航天器某时刻发生碰撞可能性的主要指标，在空间目标碰撞预警工程中具有重要的意义［18］。计算最大瞬时碰撞概率主要有以下3种方法：

（1）直接法［5］

直接利用数值优化技术寻找指定时间段内的最大瞬时碰撞概率，其优点是不要求目标函数光滑，也无需导数信息；但计算量较大，不能满足实时预警的需求。

（2）最大PDF法［19－20］

假设PDF在包络体内近似相等（即rA≪σ），最大瞬时碰撞概率问题转化为求包络体中心最大概率密度函数，即文献［5］定义的拟最大瞬时碰撞概率。当联合协方差矩阵C 各向同性时，等价于最小距离处对应的瞬时碰撞概率。当C 未知时，可根据式（1）对C 求导取极值，估算瞬时碰撞概率最大可能值。

（3）近似解析法［3，18］

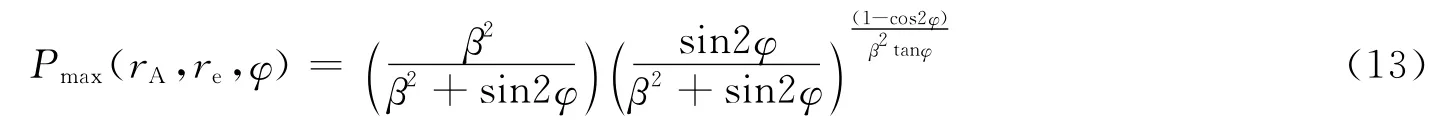
式中 β＝rA／re。由式（13）可知，瞬时碰撞概率最大值不仅与β相关，而且与椭球方向角φ 相关。

当相对位置不确定性较大时，通过式（2）计算的概率值较低，造成一种不可能碰撞的假象，即Alfano提出的“概率稀释”现象［21］。当协方差C 未知时，尽管可通过计算瞬时碰撞概率最大可能值进行保守评估，但研究表明：碰撞概率对协方差的变化比较敏感，尤其是方差小于概率极值点对应的方差值时更为突出［22］。为降低虚预警律，可采用蒙特卡洛仿真分析法估算碰撞概率，但碰撞为小概率事件，需要大量样本点（通常量级为几万～几百万），其计算代价不容忽视。

在实际应用中，考虑到计算量的问题，常联合使用几种指标分层次进行安全风险评估。随着评估精确度的提高，计算量也随之增加。文献［19］将最小距离及最大瞬时碰撞概率作为交会轨迹安全的定量评价指标。一旦追星3σ椭球与目标星控制区有交集，则需计算两星的最大瞬时碰撞概率。文献［23］将确定碰撞概率的步骤划分为估计瞬时碰撞概率、总碰撞概率及蒙特卡洛仿真分析3个层次。一旦当前层次计算结果超出门限，则需进行下一层次更精确的估计。当航天器相对距离很小（小于100m）时，建议结合最小距离进行安全风险评估［24］。

6 存在的问题及发展方向

概括起来，线性相对运动碰撞概率计算分为直接法、近似法。根据积分处理的方式不同，直接法分为极坐标下积分，沿包络体轮廓线积分和沿坐标轴一维积分。非线性相对运动碰撞概率计算采用直接法计算量较大，目前主要采用分段线性近似积分累加。现阶段航天器碰撞概率计算方法研究还存在以下问题：

1）当系统成员大于2时，如近距离编队飞行，其构形约束较强，且有一定的相对姿态，碰撞模型变得较为复杂。目前的研究大多忽略相对姿态的影响，且相对运动简化为共面圆或椭圆，对于两颗以上的航天器碰撞概率问题描述与计算还有待研究。

2）关于状态及位置误差协方差的外推公式，大多基于C－W 方程，未考虑轨道偏心率及摄动等因素的影响。对非线性相对运动，C－W 方程会产生误差积累，碰撞危险度的预测将产生偏差。尽管文献［20］采用非线性系统基于协方差分析描述函数法（Covariance Analysis Description Equation Technique，CADET）建立了考虑导航和控制偏差的相对状态及其协方差矩阵的传播模型。但由于CADET为统计模型，不能对某时刻瞬时碰撞风险进行有效指导。此外，估计的状态误差协方差本身存在不确定性。目前仅研究了线性相对运动一定假设条件下碰撞概率的置信度问题。对于非线性条件下，误差椭球的大小和形状均存在不确定性时碰撞概率置信度的评估方法还有待进一步的研究。

3）故障是威胁航天器安全的主要因素。目前对故障模式下的碰撞概率研究很少。针对“概率稀疏”现象，碰撞概率的可靠性对位置确定精度的要求有待进一步分析。当位置误差协方差未知时，为降低虚预警律，建议应尽可能在瞬时碰撞概率极值处设定不确定性进行分析研究。

4）目前为止，碰撞概率计算只考虑了位置误差的影响，根据假设精确的相对速度矢量推导相遇几何，未考虑相对速度不确定性的影响。事实上，相遇面是由相对速度定义，即便是微小的方向改变也可能使碰撞概率计算结果发生巨大变化。此外，现有的瞬时碰撞概率仅与某时刻的静态参数相关，未考虑相遇模式及相对速度对碰撞风险的影响（很显然，同一位置，两者接近的碰撞风险比两者远离的碰撞风险大）。对于机动过程中的碰撞风险评估，由于未考虑航天器是否有足够的时间执行规避机动，现有的瞬时碰撞概率计算不能满足要求。

事实上，影响航天器飞行安全的因素复杂而繁多，碰撞风险除了受导航系统影响之外，还与系统性能参数相关，比如航天器的规避控制能力，相对导航定位速率以及通信性能，甚至系统可靠性等。但目前的碰撞概率计算模型无法进行扩展，难以加入其他影响安全的因素。结合其他安全评估指标，在性能基础上研究航天器近距离飞行安全性是今后研究的方向。

［1］王继河，张锦绣，曹喜滨.分布式卫星系统自主安全管理与控制研究综述 ［J］.哈尔滨工业大学学报，2009，41（5）：1－5.WANG JIHE，ZHANG JINXIU，CAO XIBIN.Survey of autonomous safety operation and control for distributed satellite system ［J］.Journal of Harbin Institute of Technology，2009，41（5）：1－5.

［2］LELEUX D，SPENCER R，ZIMMERMAN P.Probability－based space shuttle collision avoidance：Space OPS 2002 Conference，Texas，October 10－11，2002 ［C］.

［3］CHAN F K.Spacecraft collision probability［M］.California：The Aerospace Press，2008.

［4］白显宗.空间目标碰撞预警中的碰撞概率问题研究 ［D］.长沙：国防科学技术大学，2008.BAI XIANZONG.Research on collision probability in space objects collision detection ［D］.Changsha：National University of Defense Technology，2008.

［5］王华.交会对接的控制与轨迹安全 ［D］.长沙：国防科学技术大学，2007.WANG HUA.Control and trajectory safety of rendezvous and docking ［D］.Changsha：National University of Defense Technology，2007.

［6］COPPOLA V T，WOODBURN J，HUJSAK R.Effects of cross correlated covariance on spacecraft collision probability：AAS／AIAA Space Flight Mechanics Meeting，Maui，February 8－12，2004 ［C］.Reston：AIAA Inc.，2005.

［7］FOSTER J L，ESTES H S.A parametric analysis of orbital debris collision probability and maneuver rate for space vehicles，NASA／JSC－25898 ［R］.Houston：NASA Johnson Space Center，1992.

［8］PATERA R P.General method for calculating satellite collision probability［J］.Journal of Guidance，Control and Dynamics，2001，24（4）：716－722.

［9］PATERA R P.Calculating collision probability for arbitrary space－vehicle shapes via numerical quadrature［J］.Journal of Guidance，Control，and Dynamics，2005，28（6）：1326－1328.

［10］ALFANO S.Review of conjunction probability methods for short－term encounters：Proceedings of the AAS／AIAA Space Flight Mechanics Meeting，Sedona，January 28－February 1，2007 ［C］.San Diego：Univelt Inc.，2007.

［11］CHAN F K.Short－term vs.long－term spacecraft encounters：AIAA／AAS Astrodynamics Specialist Conference，Providence，August 16－19，2004 ［C］.Reston：AIAA Inc.，2004.

［12］PATERA R P.A method for calculating collision probability between a satellite and a space tether ［J］.Journal of Guidance，Control，and Dynamics，2002，25（5）：940－945.

［13］PATERA R P.Collision probability for larger bodies having nonlinear relative motion［J］.Journal of Guidance，Control，and Dynamics，2006，29（6）：1468－1471.

［14］ALFANO S.Satellite collision probability enhancements［J］.Journal of Guidance，Control and Dynamics，2006，29（3）：588－592.

［15］ALFANO S.Addressing nonlinear relative motion for spacecraft collision probability：AIAA／AAS Astrodynamics Specialist Conference and Exhibit，Keystone，August 21－24，2006 ［C］.Reston：AIAA Inc.，2006.

［16］CHAN F K.Spacecraft collision probability for long－term encounters［J］.Advances in the Astronautical Sciences，2004，116（suppl.）：1－18.

［17］MCKINLEY D P.Development of a nonlinear probability of collision tool for the earth observing system：AIAA／AAS Astrodynamics Specialist Conference and Exhibit，Keystone，August 21－24，2006 ［C］.Reston：AIAA Inc.，2006.

［18］白显宗，陈磊，唐国金.基于显式表达式的空间目标最大碰撞概率分析 ［J］.宇航学报，2010，31（3）：880－887.BAI XIANZONG，CHEN LEI，TANG GUOJIN.Space objects maximum collision probability analysis based on explicit expression ［J］.Journal of Astronautics，2010，31（3）：880－887.

［19］LUO Y，LIANG L，WANG H，et al.Quantitative performance for spacecraft rendezvous trajectory safety［J］.Journal of Guidance，Control，and Dynamics，2011，34（4）：1264－1269.

［20］梁立波，罗亚中，王华，等.空间交会轨迹安全性定量评价指标研究 ［J］.宇航学报，2010，31（10）：2239－2245.LIANG LIBO，LUO YAZHONG，WANG HUA，et al.Study on the quantitative performance index of space rendezvous trajectory safety［J］.Journal of Astronautics，2010，31（10）：2239－2245.

［21］ALFANO S.Relating position uncertainty to maximum conjunction probability［J］.Advances in the Astronautical Sciences，2003，116（1）：757－766.

［22］ALFRIEND K T，AKELLA M R，FRISBEE J，et al.Probability of collision error analysis ［J］.Space Debris，1999，1（1）：21－34.

［23］PHILLIPS M R，GELLER D K，CHAVEZ F.Procedure of determing spacecraft collision probability during orbital rendezvous and proximity operations：21st AAS／AIAA Space Flight Mechanics Meeting，New Orleans，February 13－17，2011 ［C］.San Diego：Univelt Inc.，2011.

［24］CHAN F K.Miss distance－generalized variance non－central Chi distribution：21st AAS／AIAA Space Flight Mechanics Meeting，New Orleans，February 13－17，2011 ［C］.San Diego：Univelt Inc.，2011.