无金标准条件下含协变量的ROC曲线估计方法*

刘 妍 王红宇 田娇妮 刘桂芬△

无金标准条件下含协变量的ROC曲线估计方法*

刘 妍1王红宇2田娇妮1刘桂芬1△

目的阐明无金标准条件下，考虑协变量后估计ROC曲线的两部贝叶斯模型。方法 介绍两部贝叶斯模型，结合实例，筛选无金标准条件下ROC曲线的影响因素，考虑协变量影响后，估计ROC曲线。结果 两部贝叶斯模型不仅可探讨协变量对疾病状态的影响，而且可探讨协变量对诊断试验结果的影响，同时可计算不同协变量取值条件下ROC曲线下面积。结论 两部贝叶斯模型可有效地解决无金标准条件下，考虑协变量影响的ROC曲线估计问题。

两部贝叶斯模型 ROC曲线 无金标准 协变量

*：国家自然科学基金项目(编号81172774);山西省自然科学基金项目(编号2009011005-2)

1.山西医科大学卫生统计教研室(030001)

2.山西医科大学第二医院

△通讯作者：刘桂芬，E-mail：liugf66@gmail.com

诊断试验是临床研究的重要组成部分，它可在筛检试验的基础上，进一步把患者、疑似病例和需鉴别的其他疾病区别开来，且病人的疗效评价、预后估计等在一定程度上也都依赖于诊断试验，所以科学地评价诊断试验，可提供给患者关于疾病的可靠信息、影响医生制定治疗计划，有效避免不必要的资源浪费。受试者工作特征曲线(receiver operating characteristic curve，ROC曲线)是目前评价诊断试验常用的一种方法，有关含协变量的ROC曲线分析，一般方法都必须基于金标准存在的假设。然而在许多疾病状态下，由于“金标准”不存在或十分昂贵或执行起来不符合实际，有时很难甚至不可能建立一个权威的“金标准”。这使在许多ROC曲线分析中，不自觉地采用不完善评价诊断试验标准，从而导致估计的ROC曲线估计偏差加大。

本文拟阐明一种无金标准条件下考虑协变量影响后，估计ROC曲线的方法——两部贝叶斯模型，它可在考虑协变量对疾病状态影响的同时，考虑协变量对诊断试验结果的影响，并可计算不同协变量取值条件下ROC曲线下面积(AUC)，从而进行不同试验准确度的比较。

两部贝叶斯模型原理

两部贝叶斯模型(two-part bayesian model)首先筛选影响疾病状态的协变量，该过程可用logistic回归模型来拟合;第二个过程即筛选影响试验结果的协变量，该过程可采用线性模型来拟合。

随机抽取含量为n的样本，设第i个个体(i=1，…n)，Di(Di=0或1)为其客观但未知的二分类疾病状态，Ti为目标诊断试验的试验结果，Ri为采用不完善标准(参照试验)进行诊断的试验结果(Ri=1：阳性，Ri=0：阴性)。假定两试验相互独立，即在Di条件下Ti与Ri相互独立。

对于第 i个个体，设有 K 个协变量 Xi，1，…，Xi，K，可能影响疾病状态Di或目标诊断试验结果Ti，或者二者都受影响。令 Xi=(1，Xi，1，…，Xi，K)'，为筛选影响疾病状态的协变量，建立logistic回归模型，定义为：

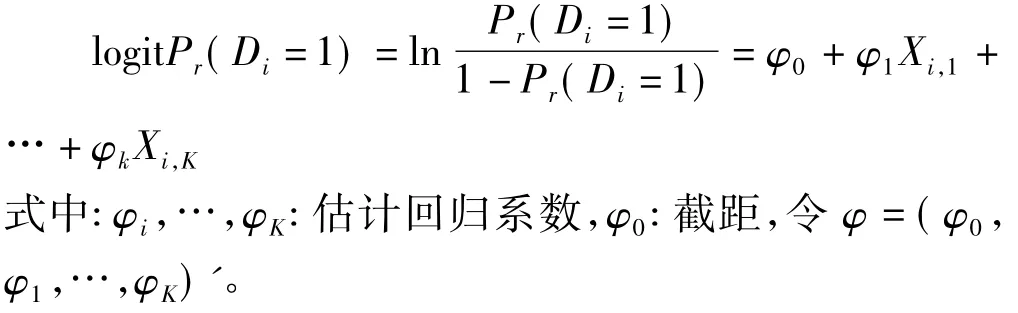
为筛选在Di条件下，影响目标试验结果Ti的协变量，建立Ti条件均值线性模型，记作：

式中：p：任意截断点处的(1-特异度)，α={E(Ti|Di=1)-E(Ti|Di=0)}/σD，β = σH/σD，由此计算得到的ROC曲线下面积记作：

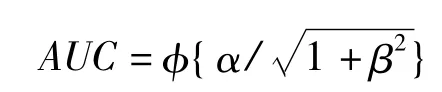
对于参照试验结果Ri，建立自然误分类模型(naturemisclassification model)，模型如下：

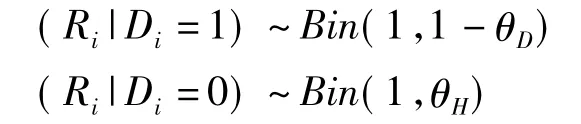
式中：θD和θH：该参照试验的假阴性率和假阳性率，二者同样也是未知的。对于第i个个体，Di、Ti与Ri的联合似然函数表示为：

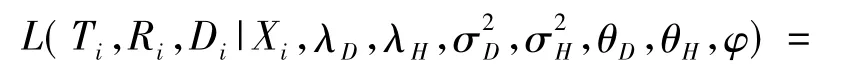
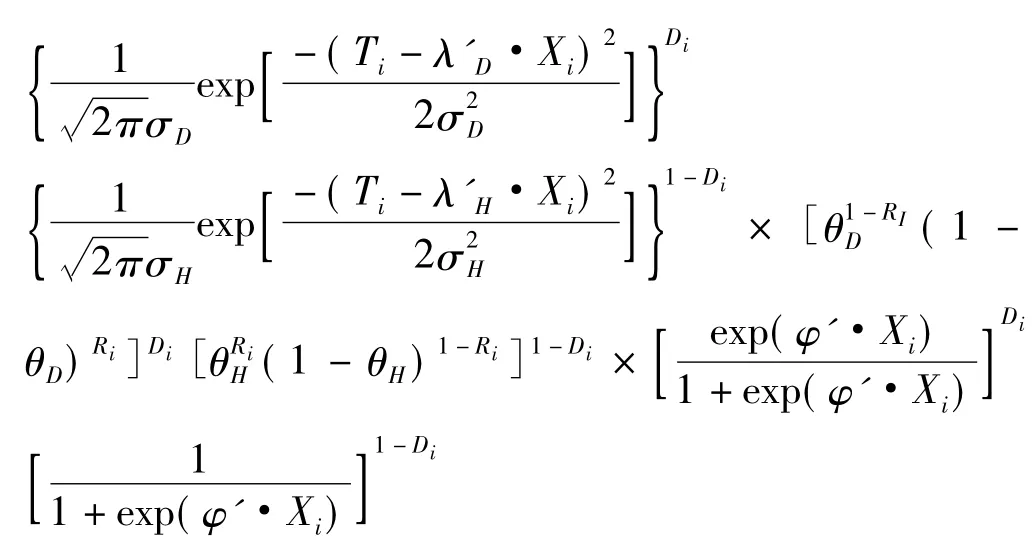
为每个参数设定先验分布，假定 λD、λH、1/σ、1/σ、θD、θH和 φ 的先验分布相互独立。对于每个 λD，0，λD，1…λD，K、λH，0，λH，1…λH，K和 φ0，φ1…φK选用正态无信息先验分布 N(0，1000)，1/σ和 1/σ选用伽马无信息先验分布γ(0.001，0.001)，θD和 θH选用贝塔无信息先验分布β(0.5，0.5)。根据先验分布和似然函数，采用MCMC方法得出后验分布的参数估计值。本研究使用Gibbs抽样构造马尔科夫链来模拟参数的后验分布，得到所有待估参数的完全条件分布。根据估计获得的模型参数，绘制出协变量取值分层的多条ROC曲线，并计算相应的ROC曲线下面积，进而准确地评价该指标分层诊断的价值。整个过程应用MATLAB7.8实现。

模拟研究

在金标准D和参照标准R对应的θD、θH均已知的情况下进行模拟，随机产生服从两部贝叶斯模型要求的随机变量T，条件均值结构为

式中，X1，X2均服从均匀分布，X1，X2～ U(0，1)，(T|D=1)，(T|D=0) ～ N(0，1)。取 θD=0.1，θH=0.2 进行模拟研究，采用两部贝叶斯模型进行分析，取无信息先验分布(如前文)，模拟50000次，退火算法(burnin)迭代次数取5000次，退火后迭代次数即 Monte Carlo样本量为45000，参数估计结果见表1和表2。

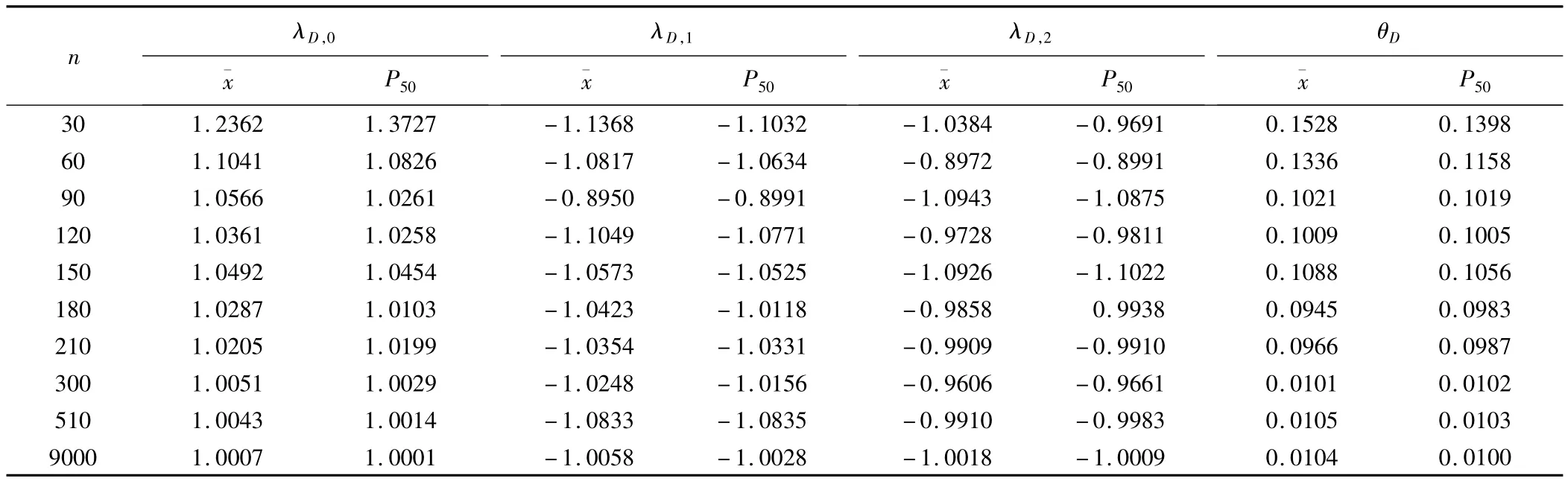
表1 两部贝叶斯模型模拟研究参数估计结果分析(1)

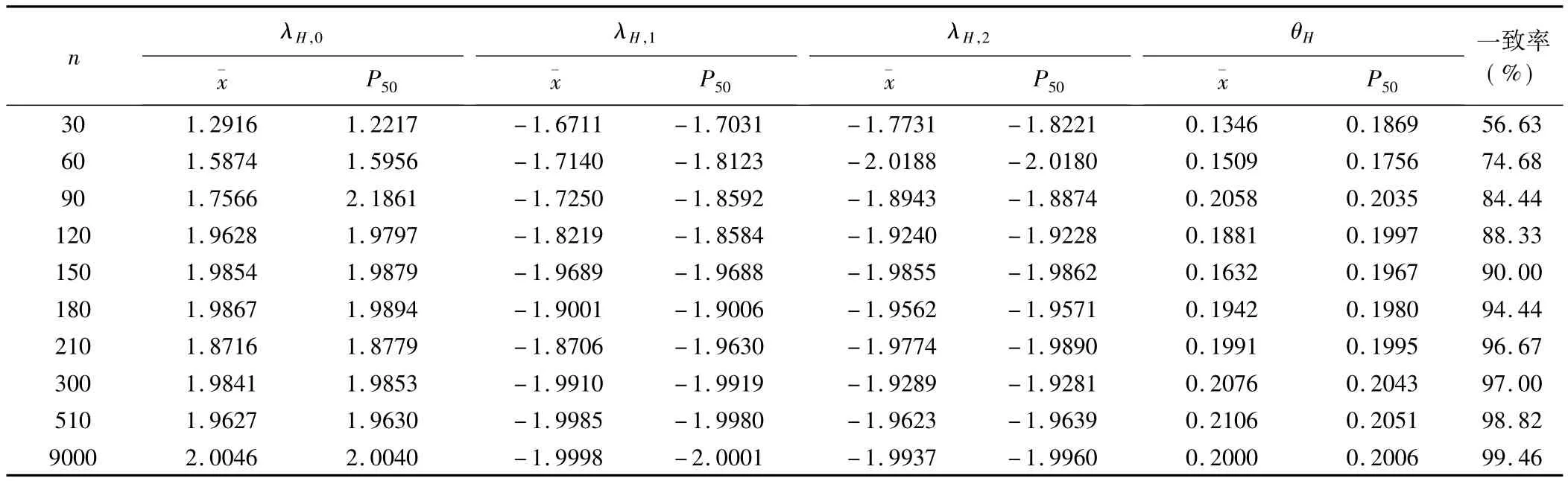
表2 两部贝叶斯模型模拟研究参数估计结果分析(2)

由表模拟结果可见：(1)随样本含量的增加，参数估计的准确度越来越好，当样本含量增加到150时，参数估计值与真值接近，但Chong Wang等人研究表明，为了将居住环境、生活习惯等混杂因素对诊断结果的影响降到最小，应在允许的范围内尽量抽取不同居住地、不同生活习惯的样本，也即尽可能增大样本含量。(2)两部贝叶斯估计的中位数和均数虽相差不大，但中位数更接近真实值。(3)在样本含量低于100时，模型估计得到的值与设定的真实值的一致率不足85%;当样本含量逐渐增大到150时，二者的一致率达90%;当样本含量大于300时，参数估计结果几乎与真值接近。由此可见，两部贝叶斯模型对于无金标准条件下考虑协变量后的ROC曲线估计，方法可行，结果准确，样本含量在150例以上，诊断试验准确度更高。

实例分析

国际公认只有冠状动脉造影(CAG)才是冠心病诊断的金标准。但由于CA G术是利用导管对冠状动脉解剖进行的放射影像学检查，属一种创伤性介入诊断技术，患者依从性较差，这为接受冠心病的诊断试验带来困难。欲在未进行CAG检查条件下，正确地对冠心病做出诊断，本研究收集了有临床症状自我感觉不适的疑似冠心病患者168例，检测其收缩压、甘油三酯含量，并以心电图作为参照标准。以24h动态心电图(Holter)中心率变异指标——窦性心搏RR间期标准差(SDNN)，作为诊断区分冠心病的主要指标。收集分析数据与统计描述结果见表3。

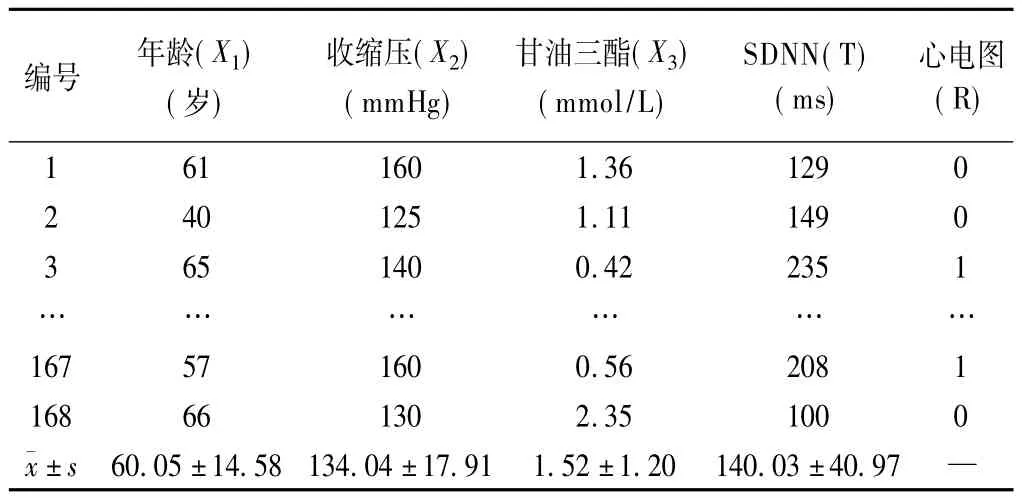
表3 168例疑似冠心病患者部分检测结果及统计描述表

采用MCMC法进行模型参数估计，先验分布选取无信息先验，如前文，模拟50000次，退火算法迭代次数取5000次，退火后迭代次数即Monte Carlo样本量为45000，按所得金标准分组的统计描述及分析结果见表4和表5。

表4 168例疑似冠心病患者各指标统计描述(±s)

表4 168例疑似冠心病患者各指标统计描述(±s)

指标 冠心病患者(n=53) 非冠心病患者(n=115)31收缩压(mmHg) 138.47±19.24 131.99±16.96甘油三酯(mmol/L) 2.14±1.55 1.23±0.87 SDNN(ms) 118.30±42.83 150.04±36.年龄(岁) 62.08±15.10 59.11±14.07

表5 SDNN诊断冠心病参数估计结果

由表5结果可见，参数φ2和φ3的95%可信区间未包括0，可以认为收缩压和甘油三酯含量是影响冠心病患病与否的因素，两指标95%可信区间均大于0，表明冠心病患者组的收缩压和甘油三酯含量均高于对照组;λD，3和 λH，3的 95% 可信区间未包括 0，表明甘油三酯含量对SDNN诊断冠心病有影响，二者均小于0，表明甘油三酯含量越高，对应的SDNN值越小，心率变异越小。同时，尚不能认为协变量年龄和收缩压是心率变异SDNN诊断冠心病时的有意义因素。

若以甘油三酯含量分层，绘制相应的ROC曲线(见图1)可见，甘油三酯含量越高，相应的ROC曲线下面积越大;AUC分别为0.7965、0.8359和0.8792，变化较为明显，表明甘油三酯含量在SDNN诊断冠心病方面，对诊断结果准确性有较大影响。甘油三酯含量偏离正常值越远，SDNN用于冠心病诊断的准确性就越高。

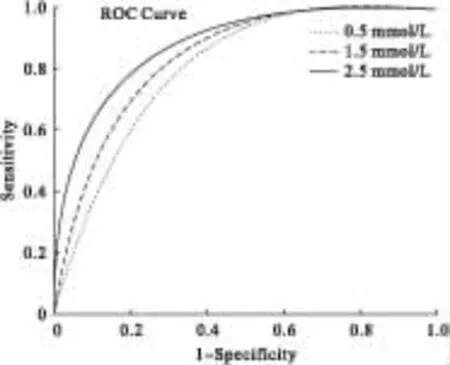
图1 不同甘油三酯下SDNN诊断冠心病的ROC曲线

讨论与小结

1.两部贝叶斯模型对于无金标准条件下考虑协变量后的ROC曲线估计，方法可行，结果准确

模拟研究结果表明，随样本含量的增加，两部贝叶斯模型对于无金标准条件下考虑协变量后的ROC曲线估计，参数估计的准确度越来越好，当样本含量增加到150时，参数估计值与真值接近。在样本含量低于100时，模型估计得到的值与设定的真实值的一致率不足85%;当样本含量逐渐增大到150时，二者的一致率达90%;当样本含量大于300时，参数估计结果与真值接近。

2.两部贝叶斯模型作为无金标准条件下的诊断试验模型，可较好地解决冠心病的诊断问题

24 h动态心电图(Holter)作为无创检查很易被大家接受，但一直被临床工作者认为，不能作为有价值的诊断指标。SDNN是24 h动态心电图心率变异的一项基础指标，容易检测。实例分析结果可见，在考虑协变量对疾病状态影响的同时，考虑了协变量对诊断试验结果影响的两部贝叶斯模型，可作为无金标准条件下，冠心病诊断准确性达到80%左右的无创诊断指标。本研究将影响诊断结果的甘油三酯含量纳入模型，得到含量偏离正常值(＜1.7mmol/L)越远，诊断准确性越高的结论，解释更接近临床实际，并可计算出不同甘油三酯含量条件下，ROC曲线诊断的准确度。

3.两部贝叶斯模型对反应变量分布没有特定要求

通常的ROC分析，反应变量若不服从双正态分布，需要对数据进行转换，而两部贝叶斯模型对于反应变量不服从双正态分布的情况，可以通过改变第二个过程的拟合模型来解决，对于反应变量分布没有特定要求。

两部贝叶斯模型作为无金标准诊断试验模型，不仅可考虑协变量的影响，同时可较好地解决无金标准时疾病的诊断问题。模拟研究表明，基于MCMC算法的贝叶斯估计，参数估计结果准确。SDNN是考虑甘油三酯含量影响后，冠心病无创诊断试验稳健性更好的一项诊断指标。有关含有缺失值的两部贝叶斯模型估计，建议采用随机缺失数据多重填补后，再进行参数估计，讨论见另文。基于MCMC算法的贝叶斯估计，退火迭代次数应保证迭代链达到收敛，结果可由模拟结果迭代图来判断。若不能达到收敛，就不可进行参数估计，需考虑修正模型或者选择其他形式的先验分布(见另文)。

1.Zhou XH.Statistical methods in diagnostic medicine.New York：John Wiley ＆ Sons，2002.

2.O'Malley AJ，Zou KH，Fielding JR，et al.Bayesian regression methodology for estimating a receiver operating characteristic curve with two radiologic applications.Academic Radiology，2001，8(8)：713-725.

3.Wang C，Turnball BW，Grohn YT，et al.Estimating receiver operating characteristic curves with covariates when there is no perfect reference test for diagnosis of Johne's disease.American Dairy Science Association，2006，89：3038-3046.

4.Goetqhebenr E，liinev J，Boelaert M，et al.Diagnostic test analyses in search of their gold standard：latent class analyses with random effects.Statistical Methods in Medical Research，2000，9(3)：231-248.

5.Pepe MS.A regression modelling framework for receiver operating characteristic curves in medical diagnostic testing.Biometrika，1997，84：595-608.

6.宇传华.ROC分析方法及其在医学研究中的应用.陕西：第四医科大学(博士论文)，2000.

7.陈卫中，潘小平，倪宗瓒.Logistic回归模型在ROC分析中的应用.中国卫生统计，2007，24(1)：22-24.

Estimating Receiver Operating Characteristic Curves with Co- variates in the Absence of Gold Standard Test

LiuYan，WangHongyu，TianJiaoni，etal．TheDepartmentofHealthStatistics，ShanxiMedicalUniversity(030001)，Taiyuan

ObjectiveTo introduce the method for estimation of receiver operating characteristic curves with covariates when there is no gold standard test.MethodsTo estimate the ROC curve after considered the effects of covariates，using two-part Bayesian model screening the impact factors for the ROC curve without gold standard test.ResultsTwopart Bayesian model can detect the impact of covariates not only on disease status but also on test scores.Moreover，the areas under the ROC curve with different values of covariates could be calculated.The method was also treated as the proof of statistical analysis for clinical diagnostic test.ConclusionTwo-part Bayesian model can be effectively used to solve the problem of estimating ROC curves impacted by covariates when there is no gold standard test.

Two-part Bayesian model;ROC curve;No golden standard test;Covariate;