桥梁抗震分析中桥墩M-φ曲线的求解

刘喜平徐长玉

(1:陕西理工学院土建学院，汉中723001;2:西安铁路局延安机务段，延安716000)

桥梁是交通运输系统的枢纽工程.地震中，桥梁的破坏将导致交通中断，不仅影响人们的正常生活，而且将影响震后的救灾工作.我国是一个多地震国家，桥梁的抗震分析越来越引起人们的重视.钢筋混凝土桥墩M-φ曲线的绘制是桥梁抗震分析的一个重要步骤，该曲线的精确性直接影响桥梁抗震设计的可靠性，但因钢筋混凝土材料本身性能的复杂，很难得到精确的M-φ曲线.以往M-φ曲线得出主要靠加载试验而来，这在桥梁设计中既不经济也不现实.本文试图采用力学和数学手段，通过编制程序来确定钢筋混凝土桥墩的M-φ曲线.

1 基本理论与计算方法

在桥梁结构的弹塑性分析中，为了较精确地模拟桥墩进入弹塑性阶段后内力和变形之间的关系，对桥墩选用平面梁单元来模拟.梁单元属于杆系模型，而M-φ曲线是杆系模型中常用的恢复力模型，其中，Clough双线型、Takeda刚度退化三线型及Park模型是较为有名的代表模型.在求解结构杆单元的非线性刚度变化的分析中，又可以分为比较简单的“简化刚度法”和比较复杂的“实际刚度法”.“简化刚度法”是指对每根杆件的刚度都给以一定的模式，如图1所示.当杆端塑性铰出现以前，杆件的截面刚度为常数，当弯矩到达屈服弯矩My时，刚度立即进入另一常数.从可操作角度出发，本文采用“简化刚度法”对M-φ关系进行简化，并忽略下降段，这样结构分析将大大简化.计算中采用考虑了结构本构关系的强化段的双分量模型.所谓双分量模型［1－2］，就是假定每一根杆件由两个平行的假想杆组成:一根理想弹塑性杆和一根弹性杆，如图2所示.(a)图相当于(b)图和(c)图的叠加.图2中，杆件的刚度k是弹性分量刚度k1和弹塑性分量刚度k2叠加而成，即k=k1+k2.式中，k1=pk，k2=qk，且p+q=1.

图1 弯矩－曲率简化模型

图2 刚度双分量模型

对于一根配筋已知的构件，若已知My和Mu，根据弯矩-曲率简化模型，可按下式确定弹性刚度系数p与理想弹塑性刚度系数q.

式中，My，Mu分别为截面屈服弯矩和极限弯矩;φy，φu为相应的截面曲率.

2 计算假定及钢筋混凝土的本构关系

2.1 平截面假定

根据试验可知，截面平均应变值从加载开始直到破坏，都能较好的符合平截面假定，所以研究中假定构件正截面变形后仍保持平面，截面应变为直线分布，不考虑钢筋与混凝土之间的相对滑移.

2.2 钢筋的应力－应变关系

根据实验结果及钢筋混凝土构件受力性态，计算中受拉或受压钢筋的应力－应变关系分为弹性段、屈服平台和强化段3段.当钢筋混凝土构件形成塑性铰后，受拉钢筋即使越过屈服平台进入强化段，也只能达到不大的范围，从而强化段可以简化为直线，坡度即弹性模量E'=tgα'，按Y.Higashibata提出的E'=0.01E取用，如图3所示.

图3 钢筋应力－应变曲线

图4 混凝土应力－应变曲线

2.3 混凝土非线性应力－应变关系

混凝土受压区应力－应变关系曲线采用Hognestad关系式，如图4中曲线oab，下降段为线性.其中，σ0，ε0为最大的应力及相应的应变值;εu为混凝土的极限压应变值.一般取ε0为0.002∶0.002 5，εu为0.003 3.相应的曲线方程为:

受拉区混凝土的应力－应变关系如图4中曲线ocd，相应的曲线方程为:

3 计算原理分析

图5所示为矩形截面钢筋混凝土构件，在正截面受力作用下的截面的应变、应力分布.为方便数值计算，将混凝土截面分成有限条带，并假定每一条带上的应力均匀分布.分析中，混凝土和钢筋的应力均以压力为负，拉力为正［3］.

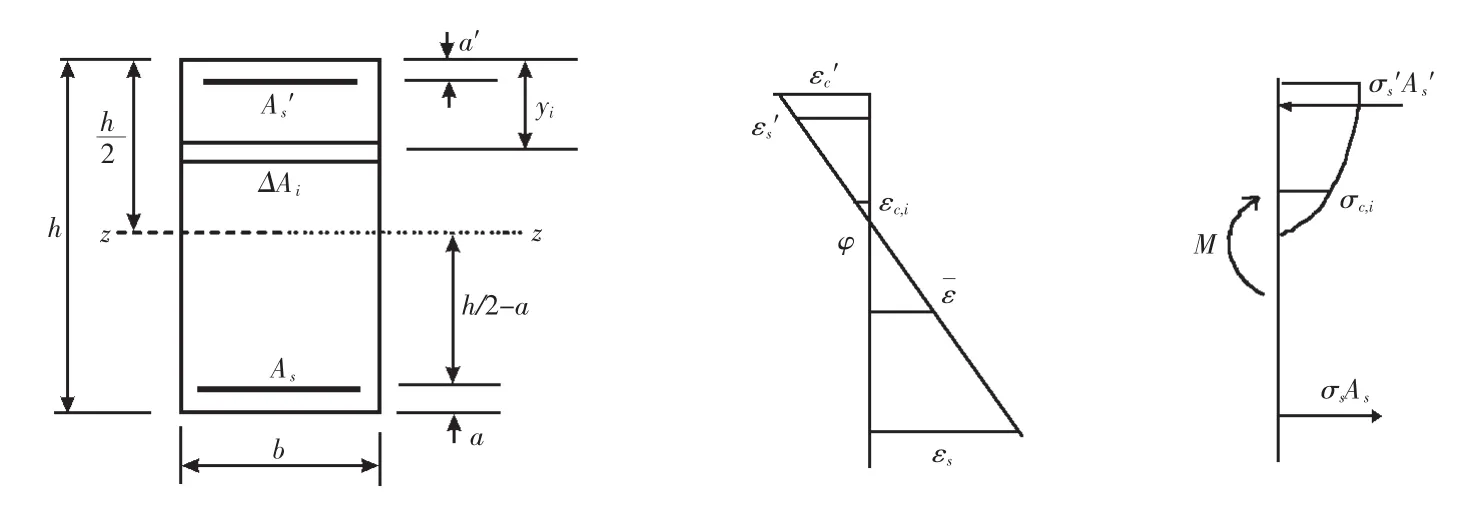
图5 矩形截面梁应力－应变

在条带划分时，为了能使计算模型中截面上的应力分布接近实际情况，一般采用多条带划分.根据平截面假定可得截面曲率为:

式中，εc'为截面受压区边缘混凝土应变;εs为受拉钢筋应变;h0为截面有效高度;φ为截面曲率.截面上任意一条条带的应变为εc，i

式中，yi为任意一条带的高度中心距截面受压区边缘的距离.

按已知的混凝土和钢筋的应力－应变关系，可得截面上任一条带的混凝土和钢筋的应力σc，i，σs'及σs，则每一条带上作用的力为:

每一条带混凝土及钢筋对截面形心的力矩为:

根据力的平衡条件可以得到:

若有轴向力作用在截面中心轴处时，上式应为:

根据力矩平衡条件有:

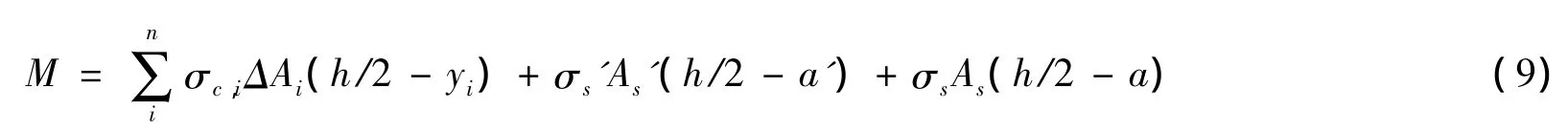
4 M-φ的数值计算与程序实现

M-φ求解，主要是求得弯矩和曲率的对应关系，因此首先从弯矩或曲率两者之间选定一个量作为已知，来确定另一个量.由于实际的M-φ曲线存在着下降段，某些区段的弯矩值对应两个曲率，为了方便起见，可先假定曲率φ为已知，然后求相应的内力，具体求解步骤如下［4－5］:

(1)令曲率φ=φ+Δφ;

(2)假定梁截面受压区边缘的混凝土应变εc';

(3)求各混凝土条带和钢筋的应变;

(4)按图3，4所示的钢筋和混凝土的应力－应变关系求出应变及相对应的应力值;

(5)按式(8)求内力总和，判别是否满足平衡条件;

(6)若不满足平衡条件，则需按下述的方法调整应变值εc'，重复步骤(3)～(5);

(7)满足平衡条件后，按式(9)求内力弯矩，从而得出φ所对应的弯矩M;

(8)循环步骤(1)～(7)，直至得出整个的M-φ关系.

在上述的计算中会遇到数值计算的逐次逼近的问题［1］.以矩形截面偏心受压为例，在轴向力N作用下第一次假定的εc'为ε1，则通过ε1求得各条带的应变值ε1，i及相应的应力σ1，i后，可求得各条带的内力总和N1.然而，ε1不可能一次假定就正好满足平衡条件:N1-N=0，而需要调整ε1.

设函数

通过调整ε，使y=0，即N'(ε)=N，则ε调整到位.

式(10)的插值函数为:

式中，y1=N1-N，y2=N2-N.要使y(ε)=0，根据式(11)，有:

按上式ε3再进行复算，看y3=N3-N→0，如果不小于某一规定值，可重复上述步骤进行运算，直到yi=N3-N接近于零.

5 实例桥墩截面M-φ曲线计算

5.1 桥墩截面参数

下面取一个桥墩的截面参数见表1，输入到自编的程序中去求解桥墩截面的曲线.

表1 桥墩的截面参数

5.2 截面的M-φ曲线

根据表1中给出的桥墩截面参数，取曲率增量Δφ=0.000 05，同时将截面划分为50等份进行数值计算，得到桥墩单元截面的M-φ曲线，如图6(a)所示.

在进行结构弹塑性反应分析时，为了简化计算，将所得的实际M-φ曲线图6(a)简化为图2所示的简化形式.根据构件截面大小和配钢筋的实际情况，计算得到:

My=0.166×105kN.m，φy=0.180×10－2，Mu=0.210×105kN.m，φu=0.634×10－1

根据简化原理得桥墩截面M-φ曲线简化模型如图6(b)所示.

图6 M-φ曲线

6 结语

本文以求解桥墩弯矩－曲率曲线为目标，用M-φ曲线简化模型中的刚度双分量模型来替代.在考虑了混凝土的非均质性和钢筋的共同作用下，通过数值计算的方法和步骤，利用FORTRAN语言编制了程序，通过程序计算得出了桥墩截面的M-φ曲线.

［1］ 吕西林，金国芳等.钢筋混凝土非线性有限元理论与应用［M］.上海:同济大学出版社，1996:100－110.

［2］ 朱伯龙，董振祥，钢筋混凝土非线性分析［M］.上海:同济大学出版社，1985:25－30.

［3］ 舒启军，赵佩君，李顺玉.基于C语言的RC梁截面M-φ曲线研究［J］.中国新技术新产品，2011(10):32.

［4］ 鞠彦忠，阎贵平，张杰，王显利.少筋钢筋混凝土桥墩M-φ曲线的计算［J］.中国安全科学学报，2003，13(10):64－66.

［5］ 张利，李子青，胡兆同，刘健新.数值法求解圆柱形钢筋混凝土桥墩的M-φ曲线［J］.西安公路交通大学学报，2001，23(3):45－48.