DVB-S2 ACM技术中的信噪比估计

杨富银，张白愚，黄 焱

(解放军信息工程大学 信息工程学院，河南 郑州450002)

1 DVB-S2 ACM技术概述

信噪比是无线通信系统中通信质量的重要衡量指标之一，在功率控制、解码截止条件的设定、自适应越区切换、自适应编码调制等很多场合，都需要精确的信噪比估计以获得最佳的性能。因此，信噪比估计是无线通信中一个重要的研究课题［1］。

2005年3 月，欧洲数字视频广播组织(Digital Video Broadcasting，DVB)发布了宽带卫星应用的第二代传输标准DVB-S2［2］。DVB-S2采用了多种信道编码和调制方案组合，它的核心技术就是自适应编码调制(Adaptive Coding and Modulation，ACM)技术。DVB-S2的ACM链路如图1所示，卫星终端对信道信噪比进行估计，然后通过回传信道向网关报告信噪比值和卫星终端支持的最有效的编码调制方案，网关根据该信道状态信息来调整调制方式和编码码率，以此来应对信道的变化［3］。因此，在DVBS2 ACM技术中，精确高效的信噪比估计对于系统性能的提高是非常重要的。

根据在接收端是否有发送数据的先验信息，信噪比估计算法可以分为数据辅助(DA)估计与非数据辅助(NDA)估计两类［4］。文献［5］对SSME，ML，SNV，M2M4，SVR等信噪比估计算法进行了总结，并进行了性能比较;文献［6］利用移动信道的功率谱特性，提出了一种基于谱分析的平均信噪比估计算法;文献［7］基于对信号的周期平稳统计量的分析，提出了一种高斯白噪声信道下的盲信噪比估计方法;文献［8］提出了一种经典的基于子空间分解的ED算法，它通过利用信号的过采样率信息构造特定维数的自相关矩阵，避免了以前的算法中对信号和噪声子空间维数的估计。

非数据辅助类估计算法具有算法复杂、收敛速度较慢等缺点，需要大量的数据来估计信噪比。而数据辅助类估计算法只需要较少的数据，并且在利用前导符号来获得均衡和同步的情况下，使用已知数据来进行信噪比估计对吞吐量并没有额外的影响，而且性能更好。因此，相对来说数据辅助类估计算法更适用于对信噪比估计的精确度要求越来越高的新一代无线通信系统［9］。

本文提出了一种基于子空间分解的数据辅助类的信噪比估计算法，对其原理进行了详细阐述，并通过仿真将该算法与文献［5］中数据辅助类的最大似然估计算法及文献［8］中经典的基于子空间分解的ED算法进行了性能分析和比较。

2 基于子空间分解的数据辅助类信噪比估计(SD)算法原理

假设系统均衡和同步的剩余误差足够小，不会对信噪比估计造成大的影响，这样就近似符合了加性高斯白噪声的条件，并且系统有完美的定时同步，那么匹配滤波器输出的采样后得到的信号可表示为

式中:sk是第k个传输的符号，其均值为0，方差为1;n(k)为独立的零均值的高斯白噪声，它的方差为σ2=;h(k)为信道的增益。需要估计的信噪比为

本文提出的基于子空间分解的数据辅助类信噪比估计算法，简称为SD算法，是利用信号协方差矩阵的特征值推导出来的。令导频符号的个数为N，每传送L个数据符号就传送1个导频符号。假设每传送L个数据符号就传送的1个导频符号就是之前传送的符号的重复，那么，成对的两个相同的连续的符号就可以称为一个块。第k个接收到的块由下面两个元素组成

在实际应用中，信道的多普勒带宽远小于信号的频率，在这样一个块的持续时段里传输信道近似保持恒定。因此，第k个接收到的块可以进行如下表示

式中:y(k)=［y(kL)，y(kL+1)］T;u=［1，1］T;hk=h(kL)≈h(kL+1);零均值高斯白噪声v(k)=［n(kL)，n(kL+1)］T，它的协方差矩阵为Cv=σ2Ⅰ2;接收块y(k)的协方差矩阵为

计算出其特征值为

显然可知，λk为最小的特征值，此类特征值张成的空间是噪声子空间，特征值λN张成的空间是信号子空间，由式(7)可得出

经过计算，可以得出

将式(10)带入式(8)，可得到如下的信噪比估计式

将式(11)带入式(12)得

3 仿真与性能分析

由文献［5］对各种信噪比估计算法的研究和性能比较，可知数据辅助类的最大似然估计(ML)算法的性能非常好。另外，文献［8］给出了一种经典的子空间分解(ED)估计算法。下面就将本文提出的算法与这两种算法进行性能对比和分析。最佳的信噪比估计应为无偏估计(或者偏差最小)，且具有最小的方差。本文定义估计偏差和标准差作为衡量算法性能的评价标准。

估计偏差定义为

标准差是方差的平方根，定义为

式中Nmc为Monte Carlo仿真次数，sqrt(·)表示求平方根，i)为第i次仿真的估计值，ρ为信噪比真实值。

设过采样率为16，Monte Carlo仿真次数为1 000，信噪比范围为-5～+25 dB，SD算法中的L=16。图2给出了当观测符号数为2 000时三种算法对QPSK信号估计的偏差和标准差。图3给出了不同观测符号数下SD算法对QPSK信号估计的偏差和标准差。图4给出了观测符号数为2 000时SD算法对不同调制方式的信号估计的偏差和标准差。

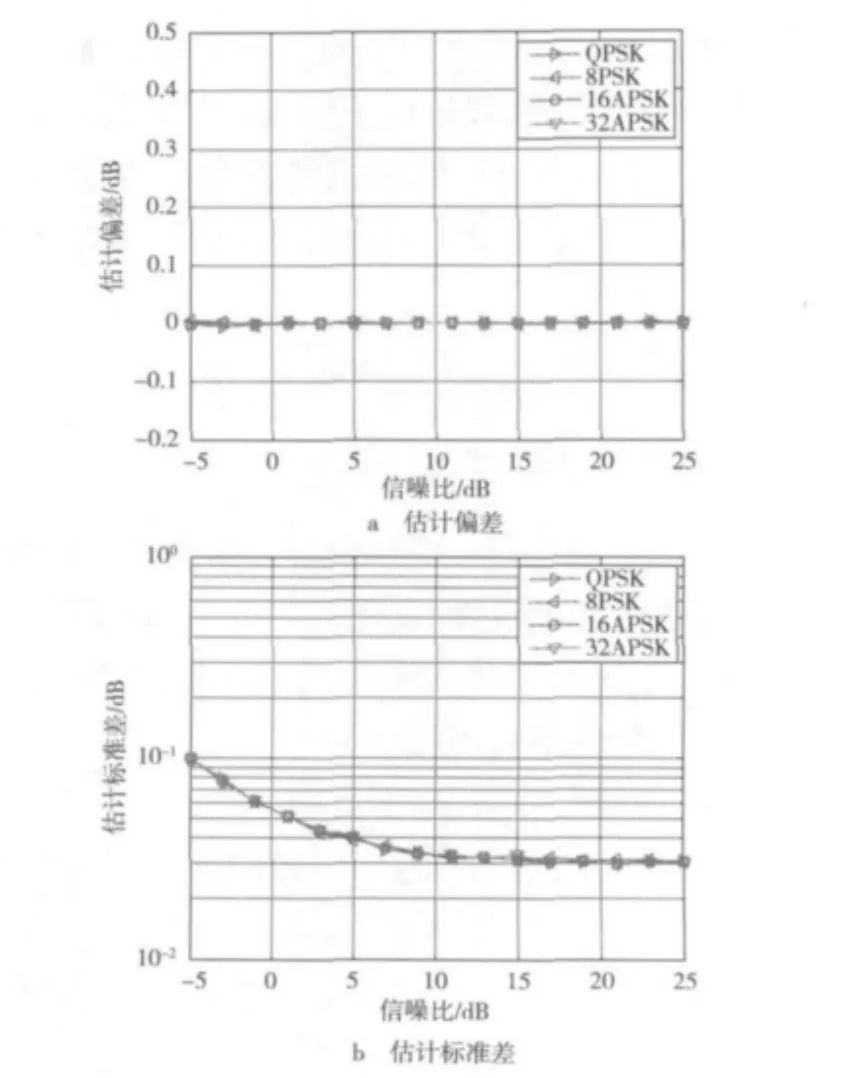
图4 符号数为2 000时SD算法对不同调制方式的信号估计的偏差和标准差

由图2a可以看出，本文提出的SD算法与文献［5］中的ML算法估计偏差都非常小，SD算法的估计偏差曲线稳定，而ML算法在信噪比较低时估计偏差曲线有稍微波动。文献［8］中的经典ED算法的估计偏差较大，效果远比SD算法和ML算法的差，而且在信噪比降低时ED算法估计偏差越来越大。由图2b可以看出，ED算法的估计标准差大于SD算法和ML算法，而且SD算法的估计标准差在任何情况下都比ML算法和ED算法的小。图2说明数据辅助类的信噪比估计算法比盲信噪比估计算法的效果更好，更适合对估计精度要求很高的实际系统。同时，本文提出的SD算法比前人研究中认为效果很好的ML算法的性能更优，估计精度更高。

图3可以看出，SD算法在观测符号数量不同时的效果不同，观测符号数越多，算法的性能越好，估计偏差和标准差越小，这是因为子空间算法是一种基于统计量的估计方法，其估计性能与观测符号个数密切相关，因此在实际应用中可根据要求的估计误差选择合适的符号数。

图4可以看出，SD算法对DVB-S2系统中所采用的QPSK，8PSK，16APSK和32APSK等调制方式的信号进行信噪比估计的结果曲线几乎完全重合，都能对信噪比进行很精确地估计，这说明该算法对DVB-S2系统中所采用的几种调制方式并不敏感，对这几种调制方式都适用。

4 结束语

本文对DVB-S2系统ACM技术中的信噪比估计算法进行了研究，提出了一种基于子空间分解的数据辅助类的信噪比估计算法(SD)，并对其性能进行了计算机仿真。研究表明，该算法在任何情况下都比数据辅助类的最大似然估计算法(ML)和经典的子空间分解算法(ED)的性能更优，计算复杂度低且具有极小的估计偏差和标准差，估计精度非常高。该算法是一种基于统计量的算法，其性能随着观测符号数的增大而提高。同时，它对DVB-S2系统中采用的四种调制方式都有较好的数值稳定性和估计准确度，非常适合该系统ACM技术中的信噪比估计。

［1］彭刚.AWGN信道中的信噪比估计算法［D］.南京:南京理工大学，2005.

［2］ETSI TR 102 376 V1.1.1，Digital Video Broadcasting User guidelines for the second generation system for Broadcasting，Interactive Services，News Gathering and other broadband satellite applications(DVB-S2)［S］.2005.

［3］方霖，雷菁，雍玲.自适应编码调制技术在DVB-S2中的应用［J］.中国有线电视，2006(17):1697-1700.

［4］龚蕾.OFDM系统信噪比估计与自适应传输技术的研究［D］.西安:西安电子科技大学，2009.

［5］PAULUZZI D R，BEAUCIEU N C.A comparison of SNR estimation techniques for the AWGN channel［J］.IEEE Trans.Communications，2000，48(10):1681-1691.

［6］华惊宇，黄清，滑翰，等.一种移动环境下的信噪比估计算法及其在多普勒频移估计中的应用［J］.通信学报，2005，26(5):132-137.

［7］花梦，朱近康，龚明.基于周期平稳的盲信噪比估计方法［J］.通信学报，2006，27(9):6-13.

［8］唱亮，汪芙平.非协作通信中的盲信噪比估计［J］.通信学报，2008，29(3):76-81.

［9］罗美玲.OFDM系统信噪比估计方法研究［D］.西安:西安电子科技大学，2007.