基于离散混沌系统的A/D转换器研究综述

刘奇峰，李清都

(重庆邮电大学 非线性电路与系统研究所，重庆400065)

1 混沌系统概述

从20世纪60年代开始，大量混沌系统的例子被数学家们所发现。在过去的50年里，动力系统的混沌特性也得到了广泛研究，对动力系统混沌特性的研究逐步从控制或者抑制混沌发展到如何有效地利用混沌。近年来，混沌许多潜在和实际的应用已被人们发现，特别是混沌在通信及信号处理中的研究更是在如火如荼地进行。例如，利用混沌进行保密通信、利用混沌对弱信号进行检测、利用混沌来产生真随机序列发生器等。最近，利用混沌检测方法，将混沌理论应用于模拟与数字系统接口的A/D转换器为混沌理论实际有效的应用指明了新的方向。

现实世界中大部分的信号是连续信号，而随着微电子技术、计算机技术和数字信号处理技术的发展，处理这些连续信号时更多的是将其转换成数字信号来进行处理。A/D转换器的目的就是将时域和幅度上连续的模拟信号转换成时域上离散、幅度上量化的离散信号。传统A/D转换器的精度一般受到无源器件和有源器件参数失配的影响，此时，如果要提高A/D转换器的转换精度，通常采用两种方法:一是使用更加精密的无源器件和有源器件;二是利用更加优化的电路结构来适配与补偿器件的误差。目前在广泛使用的高性能A/D转换器中，典型的高精度A/D转换器为(Σ-Δ)调制型，而典型的高速A/D转换器则较多采用并行技术。这两种A/D转换器要么需要数字抽取滤波器，要么需要大量高精度无源和有源的数字或模拟元件，这些元件的使用提高了电路的复杂度，加大了成本，增加了所需的功耗。因此，如何利用少量和低成本的元件来实现A/D转换成为目前人们比较关注的研究方向。Ray Brown早在1992年就提出通过利用混沌的初值敏感性来对微弱信号进行检测，并且提出具体的实现方式［1］。Michel Peter Kennedy于1995年在Ray Brown的研究基础上提出利用混沌的初值敏感性来进行A/D转化，并且给出其算法实现的框图［2］。

对初值的敏感性和参数的敏感性是混沌最重要的特征。初值敏感性的含义是指混沌系统里初始值的一个微小的变动会导致混沌轨道的长期不可预测性的巨大变化:轨道之间的距离可能从极大突然变为极小，它体现了混沌系统对初值敏感的随机性［3］。初值的敏感性说明了一个非线性系统在混沌状态下对初始值的高分辨［4］。在相关的混沌理论应用方面，混沌检测方法与传统测量方法不同:混沌方法以非平衡、不稳定作为基本特征，在非线性系统的非平衡、不稳定状态中提取并且处理信息［5］。目前混沌检测的普遍方法是利用混沌振子对同频信号的初值敏感性和对噪声的免疫能力来实现微弱信号的检测［6］。而本文所讨论的混沌测量方法是一种新型的利用混沌进行检测的方法，这种方法，也为混沌在A/D转换中的应用提供了基础。

2 现有混沌A/D转换的理论及方法

目前有关混沌A/D转换器的研究都是使用基于离散时间系统模型的非线性离散映射方法。初值信号经过离散时间系统模型的采样过程后，初值信号转换成一个个独立的离散信号。而这些转换后的信号有利于进行计算机数值计算与仿真分析，对于研究该混沌系统的轨道、周期性、稠密性和初值敏感性有着很大帮助［7］。所以，离散时间系统通常被用于混沌A/D转换上。

混沌帐篷映射(Tent map)、贝努力映射(Bernoulli map)、倒锯齿映射(Sawtooth)等映射都是目前混沌A/D转换器普遍采用的方法。m移位映射是连续的，且具有周期点集在紧致度量空间∑m内处处稠密、是拓扑传递的、对初始条件敏感依赖这3点性质。由于单边符号空间上的m移位映射和移位映射存在拓扑共轭的关系。根据Devaney混沌定义，m移位映射与移位映射都是混沌的。他们具有相同的拓扑熵，而且帐篷映射等离散映射也拥有相同的拓扑熵。这几种离散映射是混沌的。同样可以证明，这几种用于混沌A/D转换器的离散映射是在相空间里平面R2正方形上进行拉伸和压缩变换得到的，这符合拓扑马蹄映射的特点，说明它们是典型的一维混沌映射。下文将详细地分析这几种离散映射的具体的实现、应用及性能［9］。

2.1 基于混沌帐篷映射的A/D转换器

混沌帐篷映射是一种离散的非线性系统，定义为

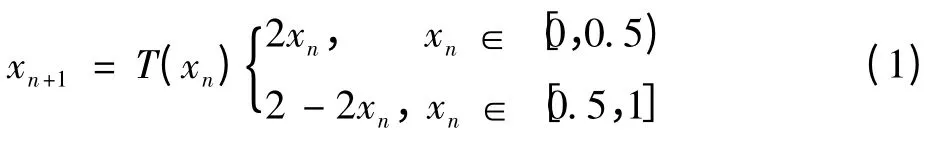
混沌帐篷映射所对应的非线性放大和线性放大的区别是:初始值从迭代开始，每次放大的倍数都不是常数，这要取决于迭代后的值所在区间。但是初始值经过混沌帐篷映射的放大后，其仍然在混沌的吸引子以内，而不会出现溢出。这种迭代的放大方式，会使帐篷映射系统的轨道进入混沌状态，可以用来对微弱信号进行检测。

假设帐篷映射系统的输入值为Vin，它对应着系统初始的状态x0，x0可通过二进制数表示为

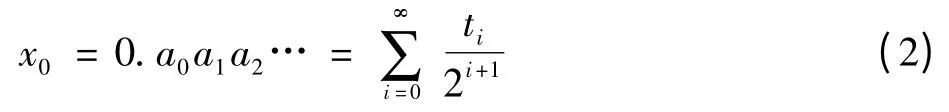
并假设gn=sgn(xn-0.5)。

在这里通过另外一种映射——Bernoulli映射来实现帐篷映射的迭代输出与初始状态x0的关系。其映射关系式为

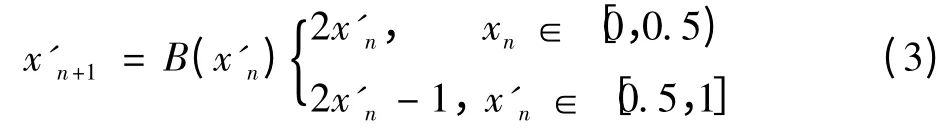
Bernoulli映射每次迭代的输出都对应着相对应的二进制比特流的一位，即xi+1=B(x'i)=0.ai+1ai+2ai+3…，这里假设bn=sgn(xn-0.5)。

由帐篷映射里的gi与bi的数学关系可以知道，gi是与bi相对应的格雷码序列，其关系为

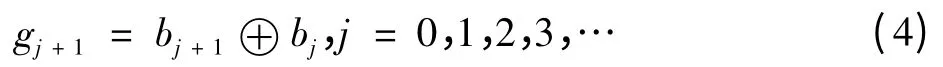
由于Bernoulli映射的初始状态x0和帐篷映射的初始状态x'0都等于输入值Vin，gi与bi可有以下关系

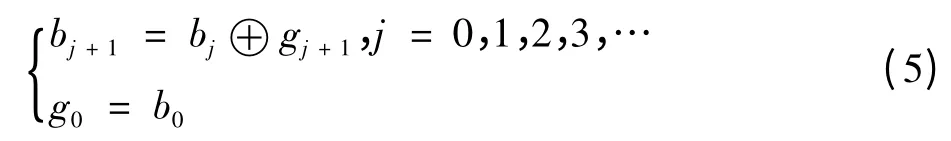
根据式(5)，可以将混沌帐篷映射的格雷码输出转换成最终需要的二进制码输出［4］。

通过帐篷映射实现的A/D转换器如图1所示，通常由比较器、D触发器、开关电容和比例延时器组成。

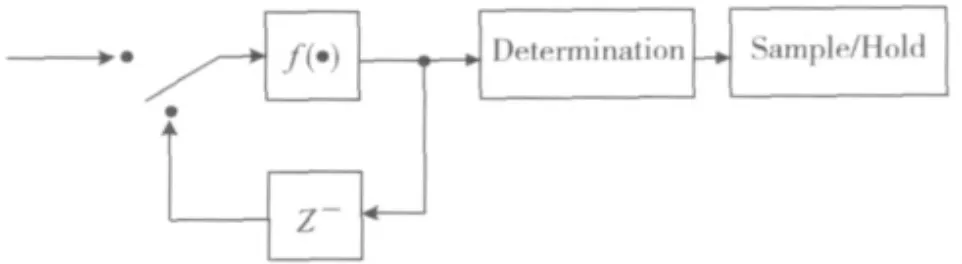
图1 帐篷映射实现的A/D转换器框图

运算放大器的输出信号即为格雷码序列gj，同时也可以得到初始条件b0，根据式(3)，可以得到所需的A/D转换后的二进制序列。基于帐篷映射的混沌A/D转换器特别适用于阵列传感器的并行信号采集系统，这类混沌A/D转换器更容易进行系统集成，降低功耗，提高分辨力［10］。

2.2 基于Bernoulli映射的A/D转换器

该类A/D转换器是直接基于Bernoulli混沌映射的，它不需要进行格雷码到二进制码的转换，所以在原理上更加直接、简单。其映射关系可见式(3)。

给定一个初始状态的值x0，经过式(3)所表示的混沌系统的若干次迭代，可以产生相对应的混沌迭代值xn。假设x0∈［0，0.5)时，定义符号ε=0，x0∈［0.5，1)时，定义符号ε=1，即

将式(6)代入到式(3)中，可以得到

通过式(7)与式(8)和后面序列的反复迭代，可以得到

通过式(9)即可推算出初始值为

其误差估计小于1/2L。

这里的Bernoulli映射，由于其混沌轨道与系统初始值存在一一对应的关系，那么可以通过符号动力学，利用其轨道所对应的符号序列计算出其轨道对应的初始值。这也是混沌测量的基本思想，此时的式(10)就可以应用于对微弱信号的检测，用得到的二进制数来推算出初始值，通过提高迭代的精度来降低对初始信号检测的误差［11］。

而式(6)组成的符号序列{ε0，ε1，ε0，…}即为所需要的模数转换的二进制序列。初始值在贝努力映射系统作用后的迭代过程如图2所示。

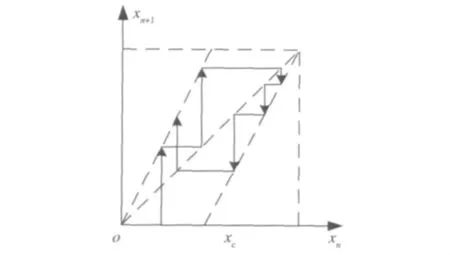
图2 初始值在贝努力映射系统作用后的迭代过程图

基于贝努力映射的混沌A/D转换器的具体实现的一般方式是通过若干运算放大器、比较器、D触发器和模拟开关这几个核心元件构成。通过时序电路对模拟开关的控制，实现电路不同拓扑结构之间的改变，最终达到对初始信号进行模数转换的效果。

2.3 基于倒锯齿(Sawtooth)映射的A/D转换器

倒锯齿映射的映射关系为

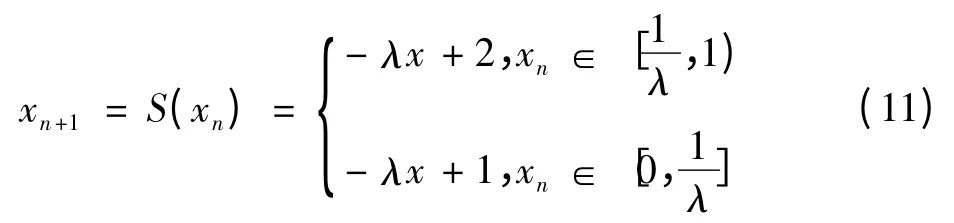
该映射产生混沌的条件是(1＜λ≤2)。同样，将定义式(11)表示的混沌系统的迭代值与符号序列形成一一对应的关系［15］

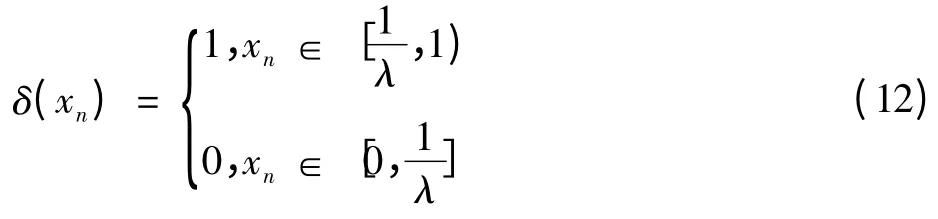
倒锯齿映射的关系如图3所示。

图3 倒锯齿映射关系图

该映射通过将［0，1］区间拉伸k倍并转回到原区间内的迭代方式将初值的轨道进行指数分离，进入混沌态［12］。在这里，一般将取λ=2来使倒锯齿映射关系用于混沌A/D转换器［15］。通过式(11)和式(12)可以用该混沌系统的迭代符号序列来表示初值为

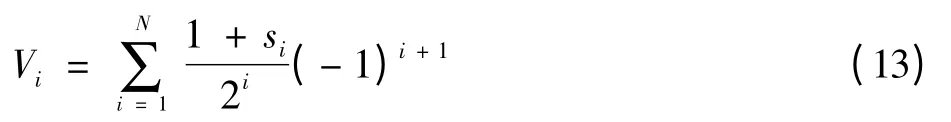
该式的量化误差为

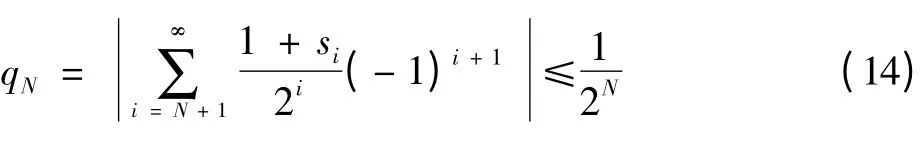
3 混沌A/D转换器的性能参数及优化方法

3.1 混沌A/D转换器电容的充放电

由于混沌映射系统迭代的实现都是通过电容上电压值的充放电完成的，所以电容容值的选取与电容性能对A/D转换的过程是非常重要的。电容上电压的充放电过程是通过积分来实现的，这里的积分时间要小于两个转换的时钟周期。

对于电容值的选取，可以通过小电容、电阻和运放组成的模拟电容网络［14］来实现电容容值的倍增。对电容值有如下两个要求:一是所组成的等效电容C的容值不超过转换临界点所对应的电容值的两倍［7］;二是待转换的初始值和转换临界点所对应的电容值不能相同。

3.2 混沌A/D转换器映射模型的轨道偏离

在第二节所述的混沌A/D转换器的几种映射模型中，往往通过电压源或者电流源的关系来确定映射图的斜率，而斜率的误差会导致混沌系统的偏离。例如在实现式(11)的电路中，斜率k是可以由两个电压源来实现的，定义实际参数值为λ，它们之间的关系为

或者，k由两个电流源实现，它们之间的关系为

如果保证系统的初值空间与符号空间是一一对应的关系［13］，那么定义k=2。

实际电路中，激励源受到运算放大器的偏置电压、偏置电流等因素的影响，参数很难达到将混沌映射转换为实际混沌A/D电路所需的严格数学值，λ会在该严格的数学值附近发生变化。λ＞2比λ＜2轨道偏离要大，因为当大于理论k时，混沌映射可能出现大于所需的2条轨道，而发生错误编码，这时就需要采用更多的符号来进行编码，并添加符号0来保证正确的编码，只要λ的偏离小于0.1%，那么混沌轨道的偏离对A/D转换的结果也不会产生明显的影响［14］。

利用混沌轨道的距离公式定义，可以得到混沌A/D转换器的编码方式，这种编码方式的优势在于混沌电路的时钟频率与积分时间常数对电路编码的检测结果不产生影响。

3.3 改进混沌映射模型来减小迭代误差

上述用于A/D转换器的混沌映射模型在数学上都是分段函数，初始值的若干次迭代也正是在分段函数之间进行切换的。在具体电路实现上，由于比较器参考电压的稳定性、精度、噪声干扰等方面的问题，会导致电路系统在判断电压值，也就是迭代过程中出现错误，从而引起映射时选择了错误的分段函数，最终导致混沌系统的发散与不稳定。

为了解决实际电路中阈值电压判断错误的问题，可以采用相伴IFS随机移位系统作为混沌A/D转换器的映射模型［17］。该系统是将原有的混沌映射的范围区域扩大，然后再重新定义混沌吸引子，该吸引子为原混沌映射系统吸引子的子集。例如式(3)表示的Bernoulii映射的混沌吸引子是［0，1］，本文想将该映射的区域扩大到［-1，1］，此时在［0，0.5］区域内有分段函数重叠，此时在电路具体判断电压值的时候会随机选择其中一个分段函数，再规定［-0.5，0.5］区间内选择确定一个分段函数，那么等效的映射模型可以定义成相伴IFS随机移位系统，新系统的吸引子为［-0.5，0.5］，是原吸引子［-1，1］的子集。新系统的边界是稳定的，可以作为混沌A/D转换器的映射模型，在具体的电路实现上，只要迭代过程中电路的参数影响保证在［-0.25，0.25］以内，由于判断时随机的选择分段函数，那么整个系统将不会发生发散和错误编码的情况［18］。

这种改进办法降低了系统的噪声对A/D转换的干扰，同时降低了整个电路对比较器参考电压的高精度的要求，提高混沌A/D转换器的在高速运行时的性能。

4 总结

本文综述了当前主流的混沌A/D转换器，分析了这些离散动力系统用作A/D转换的原理及技术特点，讨论了这类转换器的电路设计与电路性能，并论述如何优化混沌映射系统，使其更加适用于A/D转换器。

不同类别的混沌A/D转换器具体实现的一般方法是:通过对初始电压值的设置，以及对电容上电压值的混沌迭代和对混沌轨道的位置判断，最终实现模数转换。使用常用的元件和简单的模拟开关，在用于A/D转换电路时，可以实现较高的转换精度和速度，几种混沌A/D转换器均达到12位以上，如果在提高元件稳定性，提高激励性能，采用模拟补偿和数字处理的情况下，其转换精度有可能达到15～16位。此外，所讨论的混沌A/D转换器也拥有电路简单、功耗小、易于IC集成，并且其拥有集信号放大、信号采集与A/D转换于一体等诸多优点。

主流的混沌A/D转换器基本采用帐篷映射、Beinoulii映射或倒锯齿映射等离散映射，因为这类离散映射具有天生的应用于A/D转换的优势，可以采用直接应用电路实现的混沌映射方式来进行A/D转换，也可以通过改变混沌吸引子或者改变映射斜率的方式来更新以上几种混沌映射，从而减小对初始值判断的误差估计。

除了目前广泛应用的离散时间系统的混沌映射作为混沌A/D转换器的数学模型外，通过庞加莱截面转换成离散时间系统作为A/D转换器的数学模型的方法，以后还可以研究如何利用连续时间系统。

［1］BROWN R，CHUA L.Is sensitive dependence on initial conditions nature’s sensory device?［J］.International Journal of Bifurcation and Chaos，1992，2(1):193-199.

［2］KENNEDY M P.A nonlinear dynamics interpretation of algorithmic A/D conversion［J］.International Journal of Bifurcation and Chaos，1995，5(3):891-893.

［3］李明，马西奎，戴栋，等.基于符号序列描述的一类分段光滑系统中分岔现象与混沌分析［J］.物理学报，2005，54(3):1084-1091.

［4］王美娟.0.6CMOS工艺混沌A/D转换器的设计［D］.杭州:浙江大学，2006.

［5］陈素琴，袁瑞跃.多数制式混沌A/D变换器研究［J］.计量学报，2000，21(1):12-16.

［6］朱志宇，姜长生，张冰，等.基于混沌理论的微弱信号检测方法［J］.传感器技术，2005，25(5):65-68.

［7］PARESCHI F，SETTI G，ROVATTI R.A macro-model for the efficient simulation of an ADC-based RNG［C］//Proc.IEEE International Symposium on Circuits and Systems.［S.l.］:IEEE Press，2005:4349-4352.

［8］CHEN Xi，GAO Yong，ZHANG RuLiang，et al.Optimization of mapping function in chaotic ADC［C］//Proc.8th International Conference on Electronic Measurement and Instruments.［S.l.］:ICEMI，2007:913-915.

［9］李明军，李开泰.一类描述混沌映射的符号动力系统［J］.高校应用数学学报，1999，14(2):125-129.

［10］邓重一.基于混沌理论的模数转换器设计［J］.传感器技术，2005，18(3):466-469.

［11］宋爱国，李建清，黄惟.基于混沌电路的模拟式阵列触觉传感器A/D转换电路［J］.传感器技术学报，2002(1):43-46.

［12］任海鹏.基于贝努力映射和CPLD的混沌A/D转换器［J］.仪器仪表学报，2007，28(1):42-47.

［13］金文光，诸东强.混沌编码A/D转换器的原理与设计［J］.浙江大学学报:工学版，2006，40(5):796-799.

［14］邓重一，龚昌来.混沌背景下信息处理的A/D转换器原理与实现研究［J］.核电子学与探测技术，2008，28(2):330-334.

［15］金文光，王金铭.基于符号动力学的混沌信号处理研究［J］.电子与信息学报，2006，28(10):1774-1778.

［16］诸东强.混沌A/D转换器研究［D］.杭州:浙江大学，2003.

［17］HUI M Y.Chaotic coding based on symbolic sequence and its applications in A/D［C］//Proc.IEEE APCCAS 2000.［S.l.］:IEEE Press，2000:85-88.

［18］于慧敏，刘昕颖.一种基于映射结构的新颖A/D转换器的研究和仿真［J］.电子学报，2003，31(6):1378-1381.

［19］曹才开.混沌开关电容A/D转换器的设计与应用［J］.微计算机信息，2005，21(82):148-151.

［20］童勤业，钱鸣奇.混沌A/D变换器研究［J］.电路与系统学报，1999，4(1):1-5.

［21］刘昕颖.混沌AD的电路与优化设计及其性能分析［D］.杭州:浙江大学，2003.

［22］CALLEGARI S，ROVATTI R，SETTI G.Embeddable ADC-based true random number generator for cryptographic applications exploiting nonlinear signal processing and chaos［J］.IEEE Trans.Signal Processing，2005，53(2):793-805.