加强思维训练 培养思维能力

叶生树，夏 忠

（宁德市寿宁县实验小学，福建 宁德 35 5 5 00）

加强思维训练 培养思维能力

叶生树，夏 忠

（宁德市寿宁县实验小学，福建 宁德 35 5 5 00）

数学是锻炼学生思维的体操，数学教学的过程必然是培养、发展学生思维的过程。如何培养学生的思维能力呢？笔者认为抓好思维训练是关键。教材是思维的内容，课堂教学是培养学生抽象思维、概括思维、逻辑思维的主要途径。所以，要把思维训练贯穿于数学教学中，引导学生主动参与学习过程，真正使教学成为锻炼学生思维的体操。

一、加强画图能力训练，培养思维的形象性

培养学生的思维能力，首先要注意培养形象思维。画图可以把比较抽象的思维形象化，它是解决应用题的重要途径。因此，教学中要注意从直观入手，培养学生的画图能力，通过画图来形象地揭示数量之间的关系。

例如，水果店有一批水果，运出总数的5/8后，又运进700千克，现在水果店里的水果正好是原来的2/3。原来水果店的水果有多少千克？

此题的数量关系比较抽象，而根据题意画出线段图后则一目了然。

通过画图，突显了量率对应关系，学生很快就理清了思路，从不同的角度观察，得出了下列解法。

（1）从左往右观察，这批水果的〔5/8-（1-2/3）〕的差正好是700千克，故这批水果有700÷〔5/8-（1-2/3）〕＝2400（千克）。

（2）从右往左观察，这批水果的〔2/3-（1-5/8）〕的差正好是700千克，故这批水果有700÷〔2/3-（1-5/8）〕＝2400（千克）。

（3）从两端往中间观察，这批水果的〔1-（1-5/8）-（1-2/3）〕的差正好是700千克，故这批水果有700÷〔1-（1-5/8）-（1-2/3）〕＝2400(千克)。

（4）从整体上观察，这批水果的（5/8＋2/3－1）的差正好是 700千克，故这批水果有 700÷（5/8＋2/3－1）＝2400（千克）。

二、加强归纳概括能力训练，培养思维的整体性

概括也是思维活动中一个很重要的内容。如果一个人对所学过的知识不加回味和小结，那么这些知识只不过是一盘散珠。归纳概括知识恰到好处，就能把一颗颗知识的珍珠串成美丽的项链。

例如，学习了有关数的知识后，引导学生整理了这部分知识的内容，画出了图形之间的联系图。

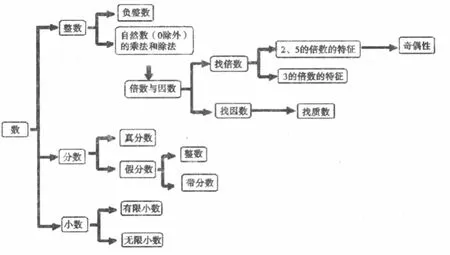
通过归纳概括，同学们对这部分知识有了整体认识，而且印象深刻。

三、加强逆向思维训练，培养思维的灵活性

解答应用题要具有多种思维方法，其中逆向的思维方法是应该让学生掌握的。逆向思维是从事物的结局出发，一步步地从后向前判断推理。

例如，新华书店卖出一批书，第一天卖出总数的1/5，第二天卖出余下的1/3，第三天卖完3200本。这批书有多少本？

这道题用顺向思维解答较难，由于题中两个分率的单位“1”不同，要统一成以总数为单位“1”。因此，要把第二天卖出余下的1/3转化为第二天卖出的占总数的（1－1/5）×1/3＝4/15，这样两个分率所依附的单位“1”才相同。根据对应法求出这批书有：3200÷〔1－1/5－（1－1/5）×1/3〕=6000（本）。为了训练学生的逆向思维，除了引导学生用顺着思路统一单位“1”，还要引导学生倒着推。从最后两个条件想，以余下的本数为单位“1”，第三天卖完的3200本，正好占余下本数的（1－1/3），求出余下的本数是 3200÷（1－1/3）＝4800（本），再往回想第一个条件，4800本正好占总数的（1－1/5），进而求得这批书有 4800÷（1－1/5）＝6000（本）。

数学中有许多关系式都是互逆的，但是可逆性联想的形成并不是很容易的，这就要求有意识地加强这方面的训练。

四、加强假设思维训练，培养思维的开阔性

为了培养学生多种解题能力，发展学生创造性思维，假设思维的训练具有极其重要的作用。

例如，甲、乙两筐苹果，甲筐苹果个数是乙筐的2/3，若从乙筐拿20个苹果放到甲筐，两筐苹果个数相等，甲、乙两筐原来各有多少个苹果？

这道题是进行假设思维训练的好素材，利用思维训练课时间让学生讨论，得出了以下解法。

（1）假设把乙筐苹果原有个数看作单位“1”，那么甲筐苹果原有个数比乙筐少1－2/3＝1/3，正好少20×2＝40（个）。因此，乙筐原有苹果个数为 40÷1/3＝120（个），甲筐原有苹果个数为 120×2/3＝80（个）。

（2）假设把甲筐苹果原有个数看作单位“1”，那么乙筐苹果原有个数是甲筐的1÷2/3＝3/2，乙筐苹果原有个数比甲筐多 3/2－1＝1/2，正好多 20×2＝40（个）。因此，甲筐原有苹果个数是40÷1/2＝80（个），乙筐原有苹果个数为 80＋40＝120（个）。

（3）假设两筐苹果个数之和为单位“1”，那么原来乙筐原有苹果个数占两筐苹果个数和的3/2+3＝3/5，后来占两筐苹果个数和的1/2。两筐苹果个数和为20÷（3/5－1/2）＝200（个），所以乙筐原有苹果个数为 200×3/5＝120（个），甲筐原有苹果个数为 200－120＝80（个）。

（4）假设两筐苹果个数差为单位“1”，那么甲筐原有苹果个数是两筐苹果个数差的 2÷（3－2）＝2（倍）。因此，甲筐原有苹果个数为 20×2×2＝80（个），乙筐原有苹果个数为 80＋40＝120（个）。

有了假设思想，就可以发展抽象思维，对解题就增加了一个思路。解题能力就是一次飞跃性的提高，假设需要勇气，假设需要摆脱一般思路，是一种大胆的设想，也是一种可贵的创造性思维。

五、加强量不变思维训练，培养思维的辨证性

在小学数学习题中，有一部分题目的特点是：不论条件如何变化，有一个量始终是不变的。为了使学生抓住这部分题目的解题关键，提高学生的思维能力，在平时的教学中有意识地建立和培养量不变的思想。

例如，甲站有汽车192辆，乙站有汽车48辆，每天从甲站开往乙站的汽车有21辆，从乙站开往甲站的有24辆，几天后甲站汽车是乙站的7倍？

解这道题需要有量不变的思想，甲、乙两站车辆对开，车辆总数192＋48＝240是不变的，抓住这个“不变量”，从问题倒推，先算出甲站汽车是乙站的7倍时，乙站的车辆应有：240÷（7＋1）＝30（辆）。由于每天乙站开往甲站的车辆比甲站开往乙站的车辆少24－21＝3（辆），可算出乙站是 30辆时需要的天数：（48－30）÷（24－21）＝6（天）。

又如，某校园里，柏树棵数是柳树的4/5，柳树若减少15棵，则柳树就是柏树棵数的7/8，原柏树、柳树各多少棵？

从题意可知，柏树前后棵数没有变，是个不变量，以柏树为单位“1”，把“柏树棵数是柳树的4/5”转化成柳树棵数是柏树的5/4，对比以柏树棵数为单位“1”的两个条件，柳树棵数和不变量柏树棵数相比，由5/4减少到7/8，就是因为柳树减少了15棵。因此，15的对应分率为 5/4－7/8＝3/8，则可求出单位“1”柏树的棵数有：15÷3/8＝40（棵），原柳树有 40÷4/5＝50（棵）。

通过以上两例，说明量不变的思想在小学数学中是存在的，应该渗透给学生。

六、加强转化思维训练，培养思维的变通性

转化思想的建立，是解答复杂应用题的重要条件。学生有了转化的思想，就能使一些无从下手的题目，化难为易，顺利解答。当然，一种思想的建立，不能企图一两节课完成，而是潜移默化地贯穿在整个教学之中。

例如，修一段公路，已修全长的3/5又15千米，剩下的公路是已修公路的1/3。这段公路长多少千米？

此题由于两个分率的单位“1”不同，若用一般的思路解，解法麻烦，解题思路难懂，学生难于接受。如果学生建构了转化的思想，就能洞察到条件之间的实质性联系，从而避繁就简，巧妙转化，获得多解。

学生在比较了含有分率的两个句式后，沟通了两个条件之间实质性联系，将“剩下的公路是已修公路的1/3”，转化成已修公路是全程的3/4，剩下的公路是全程的1/4。接通了两个条件的联系，顺利地完成了单位“1”的转化，获得下列解法：

（1）15÷(3/4-3/5)=100(千米)

（2）15÷(1-1/4-3/5)=100(千米)

（3）把一段公路分成相等的(4×5=)20份,已修的(3×5=)15份,减去已修的(3×4=)12份正好是15千米,求得每份是(15÷(15-12)=)5 千米,全程(5×20=)100千米。

（4）解：设一段公路长为 х 千米。3/4х-3/5х=15 或х-3/5х-1/4х=15。

任何自然科学的发明和创造都离不开数学。数学是一门培养思维能力的基础课。思维训练不是靠灌输，而是靠启发、引导、点拨。因此，作为数学教师要重视自身的学习和提高，发挥好点拨、引导的作用。多角度加强思维训练，积极启发学生思考，并为学生创造性思维能力的形成提供客观条件。

李雪虹）