基于LMS算法与RLS算法的自适应滤波

徐艳，李静

（长安大学 信息工程学院，陕西 西安 710064）

随着数字信号处理器性能的增强，自适应滤波器的应用也越来越常见，它主要应用于系统辨识、回波消除、自适应谱线增强、自适应信道均衡、语音现行预测、自适应天线阵等诸多领域中。自适应滤波器是根据环境的改变，使用自适应算法来改变滤波器的参数和结构。自适应滤波器算法决定了滤波的性能，根据滤波算法优化准则不同，自适应滤波器算法可分为两类基本算法：最小均方误差（LMS）算法和递归最小二乘（RLS）算法。

1 自适应滤波器的原理

自适应滤波就是利用前一时刻获得滤波器参数的结果自动的调节现时刻的滤波器参数，以适应信号和噪声未知的或随时间变化的统计特性，从而实现最优滤波。自适应滤波器实质上就是一种能调节其自身传输特性以达到最优的维纳滤波器。自适应滤波器的特性变化是由自适应算法通过调整滤波器系数来实现的。一般而言，自适应滤波器由参数可调的数字滤波器和自适应算法两部分组成。参数可调数字滤波器可以是FIR数字滤波器或IIR数字滤波器，也可以是格型数字滤波器。自适应滤波器的一般结构如图1所示[5-6]。

图1中x（n）为输入信号，通过参数可调的数字滤波器后产生输出信号y（n），将输出信号y（n）与期望信号d（n）进行比较，得到误差信号e（n）。e（n）和x（n）通过自适应算法对滤波器的参数进行调整，调整的目的使得误差信号e（n）最小。

自适应滤波器大多用FIR来实现。直接型自适应滤波器FIR滤波器如图2所示。

图1 自适应滤波器的一般结构Fig.1 General structure of adaptive filter

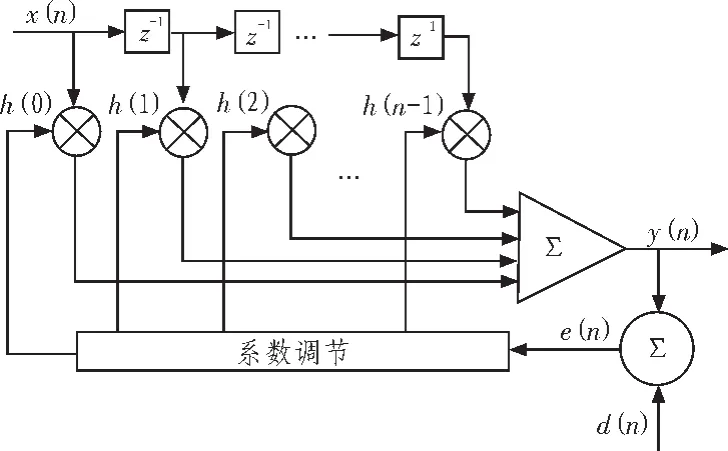
图2 直接型自适应滤波器FIR滤波器Fig.2 Direct type adaptive filter FIR filter

2 自适应滤波算法

自适应滤波器的算法主要是以各种判据条件作为推算基础的。通常有两种判据条件：最小均方误差判据和最小二乘法判据。即自适应滤波有两类基本的算法：最小均方误差（LMS）算法和递归最小二乘（RLS）算法[1]。

1）最小均方误差（Least Mean Square，LMS）算法

最小均方误差（Least Mean Square，LMS）算法是一种易于实现、性能稳定、应用广泛的算法。LMS算法设法使y（n）接近d（n），理想信号 d（n）与滤波器输出 y（n）之差 e（n）的期望值最小，并且根据这个判据来修改权系数wi（n）。均方误差ε表示为：

对于横向结构的滤波器，代入y（n）的表达式：

其中：R=E[X（n）XT（n）]为 N×N 的自相关矩阵，它是输入信号采样值间的相关性矩阵。P=E[d（n）X（n）]为 N×1 互相关矢量，代表理想信号d（n）与输入矢量的相关性。在均方误差ε 达到最小时，得到最佳权系数 W*=[ω*0，ω*1，…，ω*N－1]T它应满足下式:

求解最佳权系数W*的两种方法，一种是最陡梯度法。其思路为：设计初始权系数W（0），用W（n+1）=W（n）－uΔ（n）迭代公式计算，到W（n+1）与W（n）误差小于规定范围。其中Δ（n）的E[]计算可用估计值表达式为：

上式K取值应足够大。如果用瞬时－2e（n）X（n）来代替上面对－2E{e（n）X（n）}的估计运算，就产生了另一种算法——随机梯度法，此时迭代公式为：

LMS算法基本上是一种递推算法，它用任意选择的{h（k）}的初始值作为开始，然后将每一新的输入样本{x（n）}输入到这个自适应FIR滤波器，计算相应的输出{y（n）}，形成误差信号 e（n）=d（n）－y（n）并按方程 hn（n）=hn－1（k）+Δe（n）x（n－k），0≤k≤N－1更新滤波器系数，这里Δ称为步长参数，x（n－k）是输入信号在时间n位于滤波器的第k个样本，而e（n）x（n－k）是对第k个滤波器系数的一个梯度负值的近似估计[2]。

2）递归最小二乘（Recursive Least Square，RLS）算法

递归最小二乘（Recursive Least Square，RLS）算法是在最小均方误差算法的基础上得来的。所不同的是在求均方误差时观测数据的长度是变化的，且随着观测数据的时间先后顺序分别乘了加权因子。即RLS算法的均方误差变成:

式中：β（k，n）是加权因子，满足:0＜β（k，n）≤1，n=1，2，…，k。这样会使很多次迭代之前的数据被遗忘掉，当滤波器工作在非平稳环境中时，观测数据仍可能服从统计变化的一些特性。其中遗忘因子的最常用形式为指数加权因子，即:

式中:α是一个接近1但小于1的数。将式（7）代入式（6）可以得到均方误差的具体表达式为:

当ε（k）达到最小值时，有下列关系:

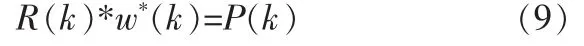
w*（k）为均方误差达到最小时的自适应滤波器最佳权系数。由式（9）可知，要求出w*（k）需要先确定。为此我们把R－1（k）当前的瞬时估计分离出来:

对于p（k）做同样的处理可以得到:

由矩阵求逆定理:若A和B是2个M×M的正定矩阵，存在关系:A=B+C*D－1*CH，其中C是一个 M×N矩阵，D是一个N×N 正定矩阵，则有 A=B－B*C（D+CH*B*C）－1。可以令 A=R（k），B=α*R（k－1），C=（k），D=1 代入上面的矩阵逆定理公式可得:

如果记:

则式（12）变形如下:

把式（15）反代入式（14）可以得到以下的关系:r（k）=R－1（k）x（k）

由式（9）得到计算权向量的公式为:

将式（15）代入式（16）右端第一项可以得到：w（k）=w（k－1）+r（k）·η（k）。

式中:η（k）=d（k）－wH（k－1）x（k）。这样就得到了权向量迭代的计算公式。

总结以上推导步骤归纳出RLS算法实现流程如下:

3 MATLAB仿真实验

1）LMS算法的自适应滤波部分实现程序代码如下：

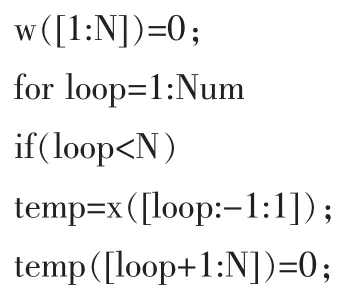
仿真结果：

图3 LMS算法的自适应滤波仿真结果Fig.3 LMS algorithm of adaptive filter simulation results

2）RLS算法的自适应滤波部分实现程序代码如下：

仿真结果：

图4 RLS算法的自适应滤波仿真结果Fig.4 LMS algorithm of adaptive filter simulation results

4 结 论

LMS算法易于实现、性能稳定、应用广泛，但LMS算法对非平稳信号的适应性差且收敛速度慢。RLS算法具有较好的收敛性能和跟踪能力，收敛速度快于LMS算法以及稳定性强，具有更小的权噪声和更大的抑噪能力，但是他的计算量很大。目前最快的RLS算法要比LMS算法多2～3倍的计算量。

LMS与RLS都是来一个数据输出一个数据，阶数和滤波系数可变，易于调整，是实际应用的实现方法。LMS的效果和步长因子μ的选取有很大关系，一般滤波器阶数越大，它的值取得越小，RLS滤波效果和λ有关，其滤波输出的信号比LMS要好一些，但运算量很大，基本是N2的数量级，而LMS运算量是 O（N）。

[1]石艳丽，谭忠吉，于海霞.基于LMS算法自适应噪声抵消系统的仿真研究[J].电子测量技术，2009（6）:71－74.SHI Yan-li，TAN Zhong-ji，YU Hai-xia.LMS algorithm based on adaptive noisecan cellation of the simulation system[J].Electronic Measurement Technology，2009（6）:71－74.

[2]严雪艳，郭建中.基于LMS自适应滤波器对噪声干扰的语音恢复研究[J].陕西师范大学学报，2009（3）:25－28.YAN Xue-yan，GUO Jian-zhong，Based on adaptive LMS noise filter to restore the speech[J].Shanxi Normal University Press，2009（3）:25－28.

[3]衡霞，刘志镜.基于自适应滤波的语音增强和噪声消除[J].微机发展，2004（1）:33－35.HENG Xia，LIU Zhi-jing.Based on adaptive filter speech enhancement and noise elimination[J].Microcomputer Development，2004（1）:33－35.

[4]张贤达.现代信号处理[M].2版.北京:清华大学出版社，2002.

[5]龚耀寰.自适应滤波器[M].北京:电子工业出版社，1989.

[6]Simon Haykin，郑宝玉，等译.自适应滤波器原理[M].北京:电子工业出版社，2006.

[7]李正周.MATLAB数字信号处理与应用[M].北京:清华大学出版社，2008.

[8]罗军辉，等.《Matlab7.0在数字信号处理中的应用》[M].北京：机械工业出版社，2005.