如何提高理论力学的教学质量和学习兴趣
张世勋,赖永星
(郑州大学力学与工程科学学院,郑州450001)
理论力学是高等工科院校重要的技术基础课程之一,它是许多后继课程如材料力学、结构力学、机械原理的基础,同时对提高学生分析问题、解决问题的能力会有极大帮助。理论力学课程本应该是一门能够激发学生学习兴趣的课程,但以笔者多年的理论力学课程教学实践,发现学生在理论力学的学习过程中,普遍缺乏学习兴趣,主要原因是理论力学的静力学,一学就会,不用理论力学方法也能完成,但遇到复杂的问题往往又做不好,这样就慢慢降低了学生的学习兴趣。如何把物理学与理论力学有机连接起来,把思维方式转换到适应理论力学的学习中,找到科学的兴趣点,是理论力学教师应当注意的问题。笔者根据多年的教学实践,在分析探讨该学科规律的基础上,提出以下几点看法。
1.理论力学相对物理中的力学是分析层次的提高
理论力学是大学物理的后续课程,于是很多同学就沿用物理学中的思维方法求解,既不规范又不严谨。因此学生普遍反映理论好懂、习题难做、考关难过。笔者认为,教师应当向学生讲明虽然物理学中的力学部分与理论力学中的内容有不少相近之处,但并不是简单的重复,而是分析层次提高了。即使对一些简单的问题,也应严格规范按照理论力学的求解方法求解。通过下面两个简单的例子,可以很好地解决学生对理论力学不正确的看法。
一群和尚一堆瓜,分不平均要打架,分一个少一个,分半个多半个。问多少和尚多少瓜。这道题对于中学生是一简单的代数题,而对于小学生却是一道难题。中学生之所以能够简单完成,是因为将和尚和瓜作为未知量看待,采用列方程的方法求解。
接着再举一如图1所示简单的力学例子。根据教学经验大部分学生都采用力的分解法求解绳子的受力,虽然也能够算出绳子的受力,但这种方法应用起来对复杂问题并不方便,甚至难以求解;而理论力学是将绳子的受力作为未知量,采用列平衡方程的简洁规范的计算方法。明确向学生指出采用物理中力学的求解方法不是我们理论力学的方法,这两种方法如同分瓜问题一个是用算术的方法,一个是用代数的方法。

图1
通过上面两个简单的例子,不但能够很好地解决学生对理论力学不正确的看法,而且也能够使学生按照理论力学严格规范的方法求解力学问题,从而慢慢地过度到复杂力学问题。
2.引导学生把握理论力学问题演变的规律
随着课程的深入,问题的复杂化,学生普遍反映习题难做,有些问题甚至难以着手,慢慢就会失去学习的兴趣。如果教师在教学的过程中,能够引导学生把握理论力学问题演变的规律,把深奥的理论讲得明白易懂,那么复杂的问题就会变得简单化。该学科中的许多问题,表面上看是不同的问题,其实遵循的却是同样的力学原理;不同的力学量的运算,遵循的也是同样的数学法则。如果学生能明白了这些,也就真正地学进去了,对这门课的兴趣也会自然形成。这样的例子在理论力学中可以找到很多。
静力学中很多看起来复杂问题都可看成由简单问题组合而成。比较图2所示的问题,可看成由一个附加在悬臂梁结构上的三铰结构组合而成。悬臂梁结构和三铰结构都属于基本的问题,如此,学生们求解起来就不会觉得复杂,好像在求两个基本的问题一样。
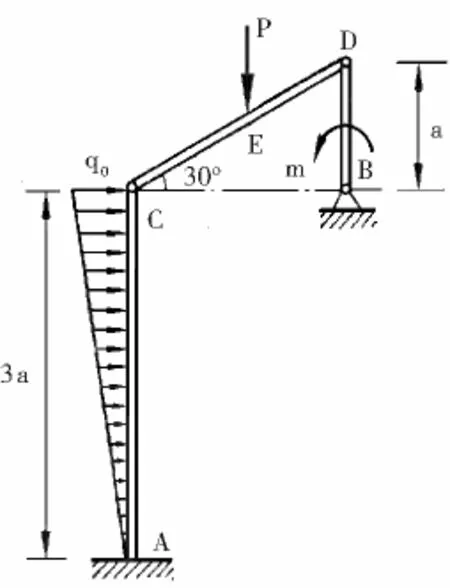
图2
运动学中点合成运动部分动点动系的选取是学生们普遍感到最为困难的问题。告诉学生为了方便求解关键是动点的相对运动轨迹易于确定。遵循动点在运动过程中始终是两个运动部件的接触点的选取原则[1],就能确保动点的相对运动轨迹易于确定,从而使问题易于求解。除个别的问题例外,大部分习题都遵循这一原则。
动力学是研究作用于物体上的力与物体机械运动之间的关系,不仅与刚体的受力和刚体的运动形式有关,而且与刚体的质量分布有关。因此,如果能将为刚体平动、定轴转动、平面运动间及结构形式相互变换[2],将会使问题求解大大简化。如图3所示为一刚体和质点组成的动力学系统,物体上刻有光滑圆槽并置于光滑水平面上,B为一质点。若图3(b)中有关的几何和质量参数与图3(a)相同,并不计杆OB的质量,则两个系统是完全等价的力学系统,其中滑块与物体A的运动规律相同。进一步地,还可演变为图3(c)所示的系统。
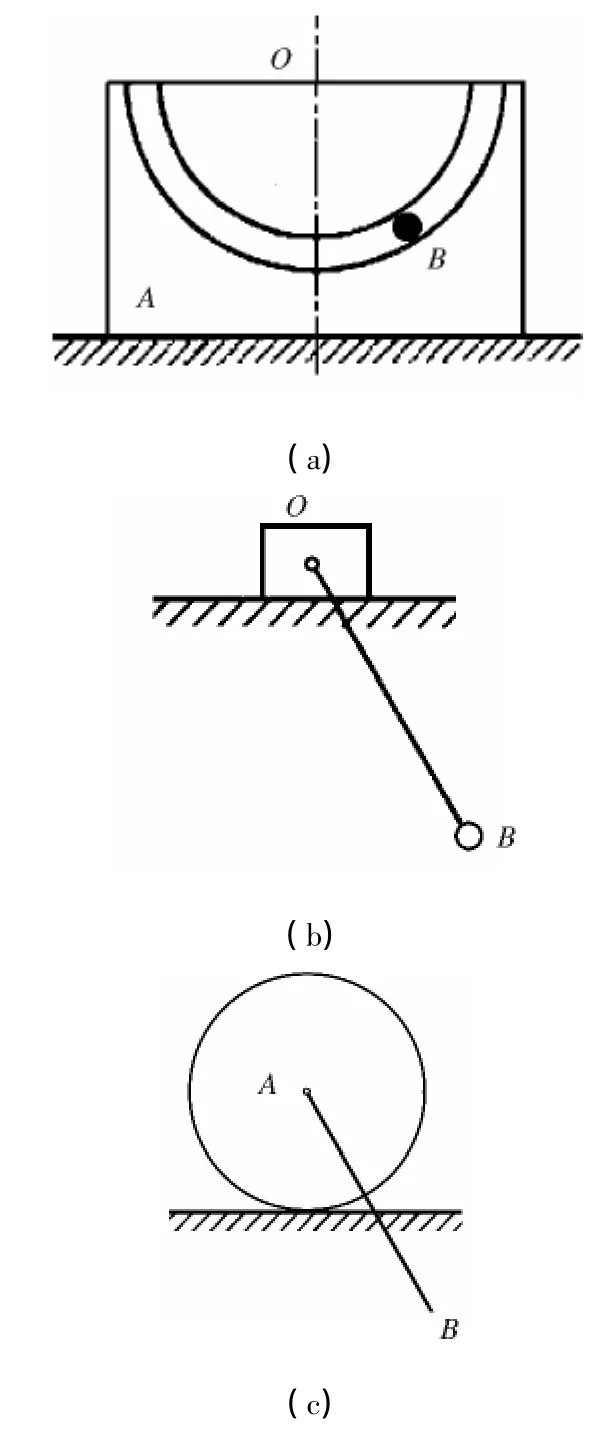
图3
再比如第三届全国周培源大学生力学竞赛理论力学题,如能掌握质量分布,运动形式的转化,将会使一复杂问题转化为一教科书中的普通习题。如图4(a)所示,已知薄方盘上有一半径为R的光滑圆槽,方盘的质量为M,质心在圆心O点处,对O的回转半径为ρ,在圆槽内有一质量为m的小球B,该系统初始时刻静止地放在光滑的水平面上,给小球一沿圆周切线方向的冲击,使小球突然有一沿圆周切线方向的初速度v0,试求此后系统的运动。[2]
根据已知条件,可知如图4中所示薄方盘作平动,因而可用一位于其质心并具有相同质量的质点来代替,注意到在运动过程中O,B两点的距离始终保持为R,故可用一不计质量的刚杆连接,于是,图4(a)等价演变为图4(b),图中黑点大小不同表示质量不同,而图4(b)是教科书中的普通习题。
3.结合历史的发展和存在的问题进行讲述
在理论力学的教学中,如能结合历史的发展和个别章节存在的问题进行讲述,就能增加学生对本课程的学习兴趣,又能锻炼学生的逻辑思维和解决问题的能力,以及对科学问题的兴趣。

图4
如虚位移原理教学中存在如下两类问题:(1)关于虚位移原理充分性的证明并不成立,主要是充分性证明存在逻辑问题[3,4]及证明方法本身具有缺陷造成的[5];(2)在理论力学中存在主动力在任何虚位移上的元功之和为零(∑fIδri=0)系统不平衡的充分条反例[6,7],如刚体定轴转动,光滑圆环上不受主动力作用或主动力沿半径方向的质点运动。在教学中如何面对上面提出的问题,我们认为还应当注意以下几点:
(1)不能回避有关虚位移原理提出的问题,否则部分用功好学的学生,一旦发现反例,容易造成误解。
(2)在教学中,可将有关虚位移原理提出的问题作为一个互动问题向学生提出。让学生主动发现或引导学生发现在虚位移原理充分性证明存在的漏洞和反例,可以锻炼学生的逻辑思维和解决问题的能力及对科研问题的兴趣。
(3)要向学生明确指出,虚位移原理是一种公理,求解静平衡问题是没有问题的。出现上面的问题是由于历史发展的原因造成的。1717年,伯努利在写给法国数学家范立刚的信中,首先发现了“虚位移原理”。1743年,达朗贝尔在《动力学》论文中,引人了假想的“惯性力”概念,把动力学问题变成静力学问题。1788年,拉格朗日又将虚功原理与达朗贝尔原理结合起来,提出了解决质点系动力学问题的普遍方程。如果先有达朗贝尔原理,然后有动力学问题的普遍方程,那么虚位移原理只能作为普遍方程特例出现,就不会出现今天的讨论。
(4)最后要告诉学生,随着课程发展如果把虚位移原理作为动力学问题的普遍方程特殊情况,是能够很好解释有关虚位移原理提出的问题。对少学时学生也要向学生讲清楚这段历史,并明确告诉学生用虚位移原理求解静力学问题是可以的。
由此可见,在理论力学的教学过程中,如果教师能够讲透该学科的内在规律,把复杂的问题清晰归类,让学生触类旁通,那么这门课其实也并不那么难学。学生把握到学科的奥秘以后,对该学科的兴趣自然也会形成。
[1]陈建平,陶秋帆,吴文龙.理论力学中动力学问题的演变与创新思维训练[J].力学与实践,2004,26(5):72 -74.
[2]李淑,童堃.关于动点动系的选择原则[J].力学与实践,1985,7(5):54 -57.
[3]刘枫.关于虚位移原理的探讨[J].江苏机械制造与自动化,1999(2):24 -35.
[4]汪思伟.虚位移原理与平衡概念[J].重庆交通学院学报,1983,5(2):111 -115.
[5]梅凤翔.关于虚位移与虚位移原理—分析力学扎记之一[J].力学与实践,1999,21(4):69 -70.
[6]钟奉俄.平衡和虚位移原理[J].西安矿业学院学报,1983(1):30-33.
[7]汪家訸.谈虚位移原理[J].力学与实践,1984,6(1):49-50.

