稳定流经验公式在贵州岩溶区抽水试验中应用探讨
曹振东,谭廷静
(贵州地质工程勘察院,贵州 贵阳550008)
稳定流经验公式在贵州岩溶区抽水试验中应用探讨
曹振东,谭廷静
(贵州地质工程勘察院,贵州 贵阳550008)
贵州岩溶区地下水勘查中,勘探开采井往往采用抽水试验中抽水量与水位降深关系的经验公式计算工作区地下水资源量及水文地质参数。评价勘探开采井水资源量可以用稳定流经验公式,但是含水层必须各向同性、均质、产状水平。在贵州岩溶区属于非均质含水层,产状一般不水平,因此利用稳定流经验公式进行计算资源量,会产生相应的误差。通过贵州省毕节地区13口井的抽水资料进行计算,分析其产生误差的原因,同时对岩溶区水资源的评价方法提出建议。
抽水试验;流量;降深;贵州岩溶区
2007年以来,贵州省为解决农村饮水困难大力开展地下水勘查,在解决饮水困难上,利用勘探开采井开采岩溶水是一条主要途径。在勘探开采井资源量评价中,长期以来一直利用稳定流经验公式,由于岩溶区的地下水往往分布极不均匀,其水文地质条件严格来说不符合稳定流抽水试验的假设。因此,在该区域利用经验公式计算资源量及相关水文地质参数势必会产生相应的误差。在此,本文根据具体抽水资料数据,通过计算结果对稳定流经验公式在贵州岩溶区抽水试验中应用的效果进行一定的探讨。
1 贵州岩溶区水文地质条件
贵州省碳酸盐岩广泛分布,岩溶水资源丰富。岩性、构造、地貌对含水层赋水性影响较大。碳酸盐中相对难溶和相对易溶地层的影响,形成部分表层岩溶泉。地质构造运动破坏了岩体的完整性,形成了不同的结构面,有利于地下水的运移、储存和溶蚀作用的进行。紧密褶皱与间隔层结合,形成许多彼此平行的岩溶带;平缓褶皱区地下水在水平和垂直方向都有较大的连续性,断层可能影响岩溶地层与非岩溶地层的接触关系,可能会出现沿断裂带发育。
降水是岩溶水的主要补给来源,在特定的地形地貌条件下,地下水的补给可能是沿裂隙、溶隙入渗补给,也可能是沿落水洞、洼地集中注入式补给。地下水的径流会受地质体产状、岩性、构造、地貌的控制,一般是沿补给区汇集,集中运移,最后受阻水岩组、阻水断层阻水排泄或者受地形切割排泄于排泄基准面。
总之,在贵州岩溶区含水层富水性受岩性、构造、地貌的影响较大,岩溶地区地下水的分布和运动,与一般的孔隙水、裂隙水相比,具有在分布上更为不均匀,和地表水的相互转化更为迅速,以及随时间有很大的变化等特点。岩溶区地下水分布极不均匀,对降雨影响反应较迅速,岩溶越发育,调蓄功能越差。
2 关于流量与水位降深关系经验公式的应用条件及计算方法
2.1 应用条件
流量与水位降深关系经验公式要求抽水试验要达到稳定状态,而形成稳定运动要在有侧向补给的有限含水层中,当降落漏斗扩展到补给边界后,侧向补给量和抽水量平衡或者在有垂向补给的无限含水层中,随着降落漏斗的扩大,垂向补给量补给增大,当它增大到与抽水量相等时,将形成降落漏斗。
稳定流的假设是含水层均质、各向同性,产状水平,厚度不变,分布面积很大,可视为无限延展;抽水前的地下水面是为稳定的,含水层的水流服从达西定律,并在水头下降的瞬间水就释放出来。
2.2 计算方法
大量抽水井的实际资料证明,常见的几种Q-Sw曲线类型有指数型、对数型、抛物线型和直线型。在实际抽水试验过程中,一般采用稳定流抽水试验,利用三次水位降深值和抽水试验流量值进行拟合计算,根据拟合误差大小,确定曲线类型及相应的地下水资源量。
然后,利用三次水位降深值和抽水试验流量值,采用裘布依稳定流公式计算含水层的渗透系数和影响半径。根据下列公式联合计算,其中承压水根据式(1)和式(2)联合计算,潜水根据式(3)和式(4)联合计算。

式中:Q为抽水试验流量;K为含水层渗透系数;Sw为抽水井水位稳定时水位降深;R为影响半径;r为距井中心距离;M为含水层厚度;H0为含水层初始水头。
3 抽水试验计算及结论
3.1 抽水试验计算
本文选取贵州省毕节岩溶区13口勘探开采井的抽水试验数据进行分析。13口井均是潜水井,具体抽水试验结果见表1。

表1 贵州岩溶区抽水试验数据
根据抽水数据计算Q-S曲线,然后对曲线进行外推后计算地下水资源量,但经验公式只能说明观测数据范围以内自变量和因变量之间的关系,严格来说是不能外推的,可是通常预告的设计降深往往大于抽水试验降深,因次希望对经验公式进行外推。一些学者指出,对于直线型经验公式外推降深不能超过最大降深的1.5倍,其他曲线类型不能超过1.75 ~3.0 倍,所以计算中直线型取 S=1.5S3,其他曲线类型取 S=1.8S3。结果见表2。
然后,利用三次水位降深值和抽水试验流量值,采用裘布依稳定流公式计算含水层的渗透系数和影响半径。结果见表3。
3.2 结果讨论
1)通过表2拟合差的对比,曲线拟合差中直线型和指数型差值较小,对数型差值次之,抛物线型差值最大。因此,利用稳定流经验公式对地下水资源量评价时,尽量选取直线型和指数型。根据计算结果可以看出,直线型和指数型的拟合误差相近,因为根据计算公式,符合直线型的一定符合指数型,直线型只是指数型的特例,所以可以合并直线型和指数型公式。2)资源量的计算结果具有随意性,就是用同一种方法、同一组数据计算,因外推计算中外推降深的取值不同而使计算的资源量不同。但在同一口井的计算中,资源量应该是一个定值。计算的结果因为外推降深不同而不同,说明人为性误差极大。

表2 抽水试验拟合误差及抽水量计算结果 L/s
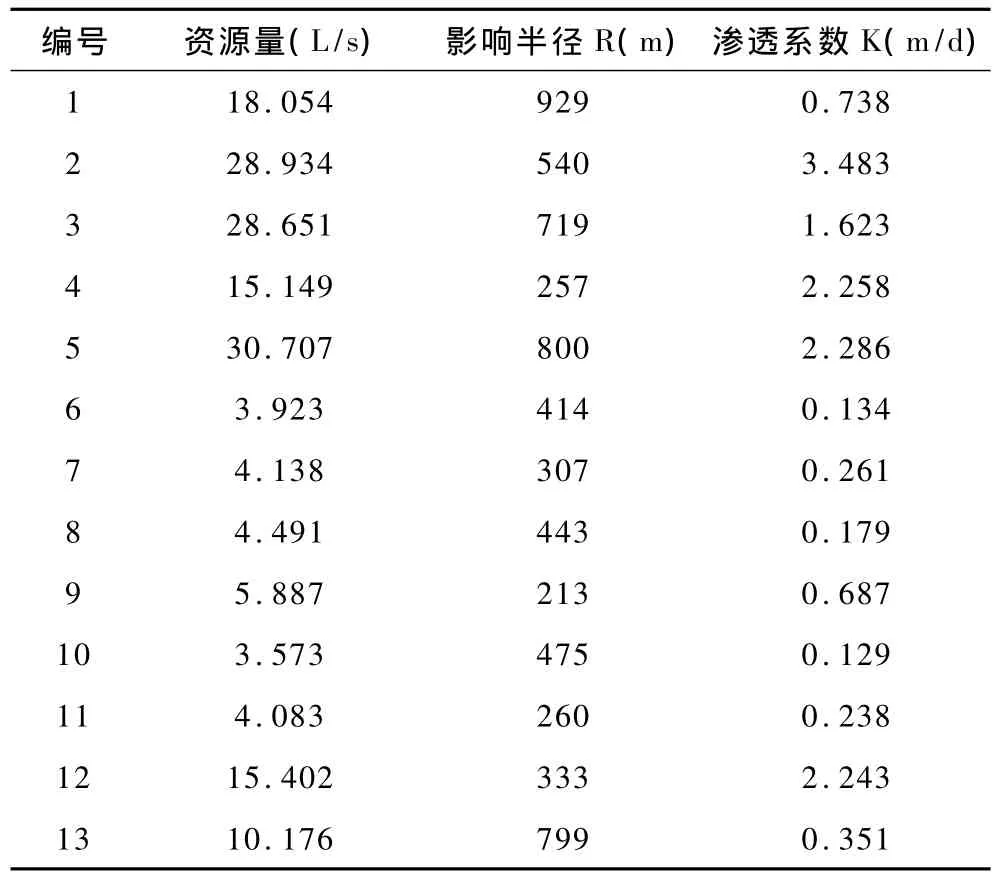
表3 影响半径及渗透系数计算结果
3)根据流量与水位降深关系的经验公式拟合方法进行计算,并不是拟合误差越小,资源量就越接近经验公式合理值,例如5号钻孔抛物线型拟合差非常大,但是计算资源量与合理值相近,说明拟合误差值和水资源计算值无相关关系。
4)由于岩溶区地下水是非均质的,各向异性的,因此采用潜水裘布依稳定流公式和联合求渗透系数和影响半径,与经验值相比误差较大。
4 建议
裘布依稳定流抽水试验的假设条件是圆形低水头,与齐姆模型的影响半径意义根本不一致, 贵州岩溶区运用流量与降深之间的经验公式不符合裘布依假设。鉴于以上原因,迫使我们选择新方法去评价井的资源量,根据贵州岩溶区水文地质特征,提出以下建议:
(1)岩溶区水文地质条件复杂,并且不符合裘布依假设,不同时期抽水资料计算的结果不尽相同,任何一次抽水试验都可能存在偏差。根据这种情况,建议采用水均衡法和地下水水文法相结合,水均衡法可以计算最大资源量,而地下水水文法可以计算枯水期可开采量,可以大大提高水量保证率。
(2)建议以最大降深抽水洗井,水位恢复后正向抽水。部分裂隙含水层内有充填物的堵塞,最大降深抽水可清洗含水层中杂质,从而保证抽水试验的正确性。反向抽水需要含水层赋水性强,导水性良好,水位降深较小并且恢复较快,每次抽水要恢复水位,并且要恢复到静水位。为了避免误差,建议选择正向抽水试验。
(3)枯水期抽水,如果可开采量很大,可根据需水量及其发展趋势进行抽水试验。如果需要计算最大允许开采量,建议进行大降深抽水试验,并且不要外推计算,从而消除人为误差,使计算的资源量比较合理。
(4)建议不求解影响半径R,因为在贵州岩溶区影响定水头的范围一般属于条带状,不符合圆形定水头假设。渗透系数是表征含水层渗透能力的值,可以利用降水时井内的水位变化,或者降水量与径流量之间的关系来求解。
[1]王大纯.水文地质学基础[M].北京.地质出版社.
[2]薛禹群.地下水动力学[M].北京.地质出版社.
[3]陈崇希.地下水不稳定井流计算方法[M].北京.地质出版社.
[4]地质矿产部水文地质工程地质技术方法研究队.水文地质手册[M].北京.地质出版社.
[5]供水水文地质学手册编写组.供水水文地质学手册[M].北京.地质出版社.
[6]左平怡.桂阳宝山西矿群孔抽水试验曲线分析[J].湖南地质.1990,9(4):57 -69.
[7]刘志峰,林洪孝,许向君等.小范围群井与单井抽水试验推求水文地质参数的比较分析[J].地质与勘探.2007,43(1):94-97.
P641.2
B
1004-1184(2012)06-0046-02
2012-10-15
曹振东(1984-),男,甘肃会宁人,助理工程师,主要从事水文地质、工程地质、环境地质工作。

