组成干涉阵列的阵元数目问题研究*

张远修，汪 敏

(1.中国科学院国家天文台/云南天文台，云南 昆明 650011;2.中国科学院研究生院，北京 100049)

二十世纪上半叶，结晶学家探讨了一种理论，可用间接方法获得图像。20世纪50年代初，英国剑桥大学卡文迪许实验室的射电天文学家赖尔等人，把这种理论发展成射电天文中的综合孔径技术，综合孔径技术的应用使得在射电波段生成了图像，这对射电天文学的发展具有重要的推动作用，赖尔也因此获得了1974年的诺贝尔物理学奖。由于在射电波段使用干涉阵列的成像过程中，试图使用接收不完全的数据恢复完整的原始二维图像信息，所以不可避免地产生一个生成图像质量的问题。人们总是试图用最小的代价和成本获得最好的效果和收益。于是，在一定的成本下如何寻找最好的布阵方案成为射电天文学家关心的问题。

由于综合孔径阵型优化设计的复杂性，目前尚未有完美的解决方案。为了简化问题，许多优化设计方案一般只考虑其中几项重要指标，如UV覆盖均匀性、旁瓣水平等。Kogan在1997年针对产生最小的旁瓣提出天线阵优化算法［1］，Boone在2001年提出了压力算法用于以减少旁瓣为目的的优化［2］。近来年，关于阵列设计和造型的研究主要集中于阵列的优化工作［3－6］。而Bonton于1999年曾指出对于二维阵列的优化没有完美的解决方案，甚至难以制定一个好的优化标准［3］，部分研究也注意到讨论关于评价标准的问题，张仙玲在2006年结合不同类型的图像指出，若频率采样点数固定，低频点越多，图像失真度越小［7］;Wenger等在2010年结合模拟干涉生成的图像质量认为，在低频分量的UV覆盖采样更加重要［8］。这些研究工作大多围绕着阵列的优化、评价等展开，而研究中一般将天线的阵元数目作为预先的设定，以此设定为前提进行阵列的优化设计工作，本文将阵元数目作为一个待解决的问题进行讨论，并利用现有的优化、评价方法为太阳低频射电阵列阵元数目的确定提供参考。

1 干涉成像模型

由于干涉阵列的设计工作大多要在阵列建设之前进行，所以综合孔径成像的过程需要在计算机上进行模拟运行，这时就需要用到干涉成像的模型。干涉成像主要基于van Cittert-Zernike定理［7］，即通过测定非相干天体目标源在出瞳面内产生的互相关强度大小，获得天体目标源的特征分布，如亮度、尺寸大小等。综合孔径成像原理为通过安置有限个数的天线组成阵列，并将任意两个天线接收到的数据进行相关处理。对于亮度分布为I(l，m)的非相干观测源，根据van Cittert-Zernike定理，在坐标分别为(x1，y1)与(x2，y2)的两天线间的相干强度为:

这是干涉成像的理论依据。下面给出在计算机上进行模拟综合孔径成像过程。假设二维天体目标源亮度分布为I(x，y)，其傅里叶频谱为V(u，v)。其中，x、y为空域坐标;u、v为频域坐标。则干涉阵列对V(u，v)的抽样函数S(u，v)可表示为:

则实际获得的频谱V'(u，v)表示为:

V'(u，v)为对V(u，v)抽样的结果。根据傅里叶变换的性质，对上式两边作傅里叶逆变换得:

为了简化，这里用FT－1符号表示傅里叶逆变换。

在计算机上做模拟成像时使用的模拟干涉成像流程如图1，首先使用实验图像模拟观测对象的亮度分布I(x，y)，对其进行傅里叶变换到频域V(u，v)，再使用S(u，v)对其进行采样得到然后进行傅里叶逆变换得到脏图，最后去卷积生成最终图像I*(x，y)。

图1 模拟综合孔径成像过程流程图Fig.1 Flowchart of simulated synthetic-aperture imaging

2 实验设计

本文工作主要源自太阳低频射电阵列计划(简称低频阵)预研究的需要，所以本文的实验以低频阵的设计需要为例进行讨论，首先介绍计划中低频阵的基本情况。

2.1 太阳低频射电阵列概况

计划中的低频阵使用基于综合孔径技术和千兆网光纤数据传输。它工作在20～600 MHz频段，时间分辨率为10 ms(快照)，频率分辨率为0.1～1 MHz可调，角分辨率约1.0～30″，灵敏度0.1 sfu。它将对太阳中高层日冕剧烈活动—耀斑、日冕物质抛射进行观测研究，在空间灾害天气实时预警预报方面，发挥不可替代的重要作用。太阳低频射电阵列的科学目标包括磁场测量、磁重联、日冕物质抛射、高能粒子加速问题，是太阳物理学中最重要研究方向，耀斑、日冕物质抛射是最重要的观测对象。射电观测提供了对日冕等离子体、瞬变过程、高能粒子加速/传输的独特诊断。该阵列的主要性能参数见表1。

表1 计划中的太阳低频阵列主要参数Table 1 Parameters of the Low-Frequency Solar Array

对干涉阵列设计的过程可以假定其观测对象是各种太阳活动，使用快照模式进行观测。另外由于天线阵列分布的几何尺度比较大，必须使用后相干的方法。天线的数目在本文中作为待定项目进行讨论。

2.2 评价方法

评价标准实际上是一个类似于价值观的问题，它决定了阵列的优化、设计的方向，也必然影响对阵元数目的研究。各种评价方法有各自的优势和缺点，没有一种完美的评价方法，所以考虑将旁瓣水平、能量覆盖率、平均方差3种代表性的评价方法分别应用于实验。3种评价方法的具体定义如下:

(1)旁瓣水平:在(7)式中h(x，y)就是对点扩散函数的定义，在点扩散函数的基础上可以继续给出旁瓣水平(Sidelobe Level，SL)的定义:

式中，δn为位于点扩散函数中心的主瓣的峰值;δm为最大旁瓣的峰值。

(2)能量覆盖率(Energy Coverage Rate，ECR):这种方法认为对大多数图像(包括综合孔径成像)而言，在傅里叶频域较为重要的部分就是能量较高的部分。由于不同观测对象的能量分布可能会有很大的差别，于是可以使用针对将来可能观测到的大量观测对象的统计，给出一个统计意义上的能量分布作为评价的依据。根据实际需求中潜在的观测对象，可以将大量与观测对象相同类型的图像累加起来，然后得到一幅统计意义上能量分布频谱:

在收集过程中，要保证这些图像的形态尽量广泛和具有代表性，进而可以认为这幅统计意义的频谱能够代表将来观测对象的频谱分布。于是，能量覆盖率在这幅统计频谱上可以定义为:

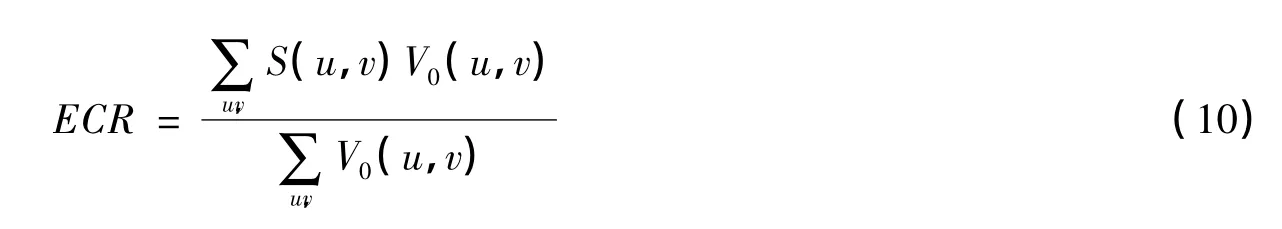
式中，S(u，v)为采样函数;Vn(u，v)是统计的频谱分布。

(3)改进的平均方差:全参考图像质量评价是将失真图像(综合孔径生成的图像)与原始图像(实验测试图像)进行比较得出图像失真的程度。在干涉成像中，原始图像就是测试图像I(x，y)，最后的生成图像可以看作失真图像，所以干涉成像的过程实际上可以看作对观测目标的某种失真过程，于是客观评价技术非常适合干涉成像质量的评价。图像客观评价技术的内容非常丰富［9－11］，文中使用一种改进的平均方差(Mean Squared Error，MSE)方法用于干涉成像的图像评价。MSE是一种最简单也是最古老的图像质量评价方法［10］，它直接将图像中每一个像素做方差然后累加，作为对图像失真程度的估计:

式中，w、h分别为图像的长和宽;n为整幅图像的像素数，即w×h。为了更适合模拟综合孔径生成的图像，需要使用像素灰度的相对值代替其绝对值。对像素灰度的相对值定义如下:

式中，mi，j是该像素在整幅图像所有像素中按灰度值进行排序后的次序;n为整幅图像的像素数。则基于排名的平均方差(Ranking MSE，RMSE)可定义为:

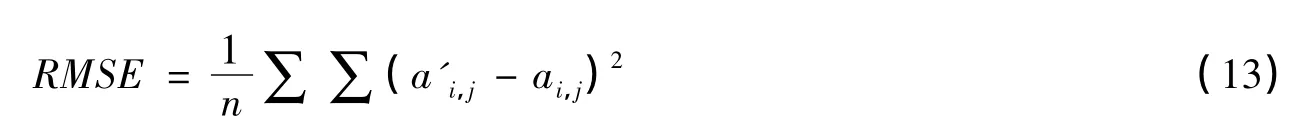
在这3种评价方法中，旁瓣水平是一种与观测对象无关的评价方法，从某种意义上讲它的结果适用于各种类型的干涉阵列阵元数目的讨论，而能量覆盖率和平均方差的评价方法与实际观测对象相关，其实验结果仅限于本文中对太阳低频阵列的讨论。评价标准的计算实际上就是作为优化算法中的适应度计算，在实验的设计中对这3种评价方法使用3个种群分别进行优化。

2.3 优化方法

由于需要对不同阵元数目情况下阵列的成像质量进行考察，这就要求不能将在某个阵元数目下的任意阵列作为该阵元数目下的代表，而需要一个最优的或接近最优的阵列的性能作为这种阵元数目下的性能代表，得到这个最优或次优的阵列需要使用优化逼近的办法一步一步地接近最优，这就是优化算法的任务。优化算法非常多，遗传算法就是一种得到广泛应用的方法，在实验中使用遗传算法进行优化。

遗传算法起源于对生物系统进行的计算机模拟研究，生物的进化过程主要通过染色体之间的交叉和变异完成。遗传算法的基本运行步骤描述如下［12］:(1)随机产生N个个体，组成初始种群，种群中每一个个体代表问题的一个候选解。然后根据优化问题，计算种群中每个个体的适应度值。(2)对种群中的个体执行交叉、变异等操作，产生新的个体，并且选择一定数量的个体形成新的种群。(3)判断是否满足算法终止条件，若满足，则输出最优解或最终种群;否则回到步骤(2)，继续循环过程。流程如图2。

遗传算法的设计过程主要考虑以下几个重要组成部分:遗传编码、适应度计算、遗传操作算子等，分别进行简单介绍并给出实验中使用的方法。

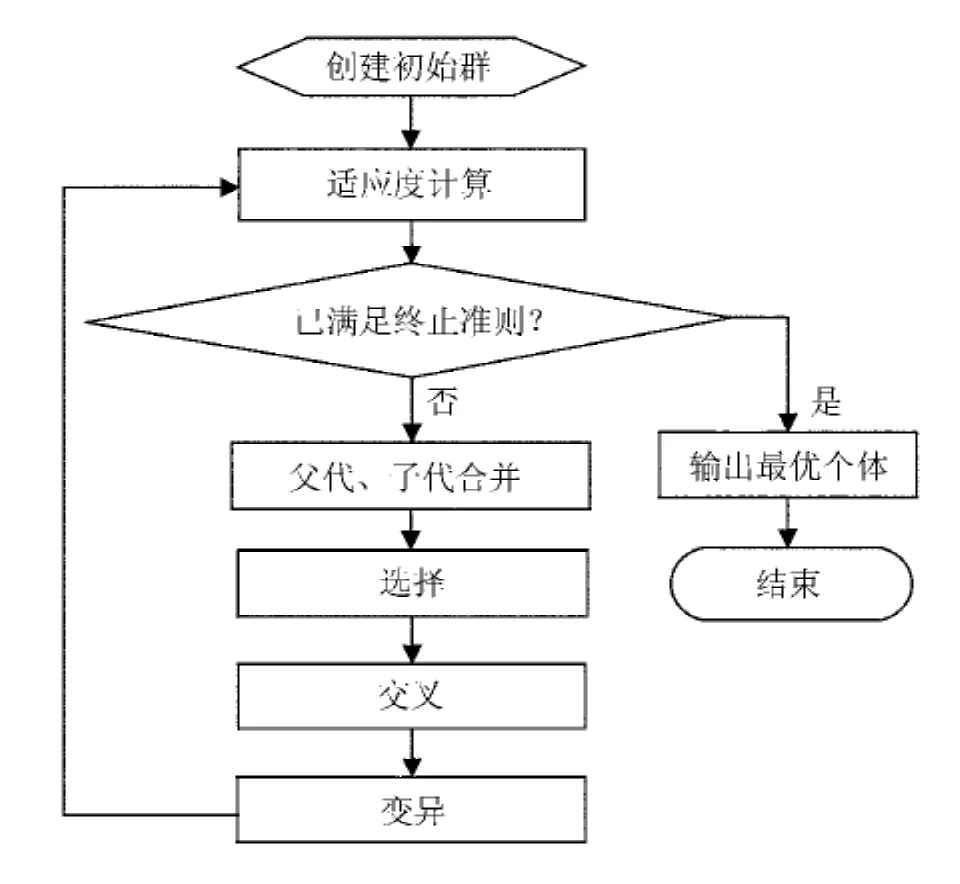
图2 遗传算法流程图Fig.2 Flowchart of the Genetic Algorithm

(1)遗传编码。遗传算法在求解优化问题时，是通过建立问题的决策变量与种群中个体之间的一一对应关系，对个体进行操作。因此，确定个体的编码与解码方式是遗传算法首先要解决的问题。不同的编码方式决定了不同的遗传操作方式。实验中使用的遗传编码方法较为简单，每个天线位置坐标的两个整数作为对每个个体的编码，如(100，127)、(212，54)等。

(2)适应度值的计算。为了遵循适者生存的原则，遗传算法需要对个体进行评价，赋予其适应度值。评价方法实际上就是适应度计算，其中能量覆盖率的指标是向上优化(越大越好)，而旁瓣水平和平均方差是向下优化(越小越好)。根据实际测试发现，对阵列优化的需要而言，使用对数的适应度变换效果较好，变换规则为a'=log(1.0+a)。其中，a为直接计算的适应度值;a'为变换后的数值。

(3)选择算子。选择算子是模拟自然选择，对种群中的个体进行优胜劣汰，从父代群体中按某种规则选取一定数量的个体遗传到下一代群体中。文中使用比例选择的方法，其中也隐含着精英保留策略，每个个体生存下去的概率为:

式中，ri为该个体在整个种群中适应度的排名;n为种群数目。

(4)交叉算子。交叉操作是生物遗传和进化的主要环节，是遗传算法区别于其它进化算法的特征。在遗传算法中，交叉算子通过模仿自然界有性繁殖的基因重组过程，将两个个体的部分基因互换，从而在产生新个体的同时，将父体的优良基因遗传给新个体。由于基因编码比较简单，所以交叉也使用普通的两点交叉方法。例如，两个体(100，127)、(212，54)进行两点交叉产生的子代为(100，54)、(212，127)。

(5)变异算子。变异操作是模拟自然界生物遗传和进化过程中，染色体上某些基因发生的突变现象。在遗传算法中，变异操作主要作用于个体的等位基因上，将某些基因位上的基因用其它等位基因替换，从而产生新的个体。一般而言，在遗传算法中，变异算子的作用没有交叉算子那么显著，执行概率取值较小。实验中使用均匀的变异算子，每一个个体的两个基因都以相同的概率变异为一个任意的合法取值。

由于实验中的计算量很大，并且讨论具有估计、估算的性质，在速度和准确性存在矛盾的情况下，更倾向于保证较快的计算速度。进行实验的阵元数目从20到100，在3种评价模式下，这样一共需要建立240个种群，每个种群规模设置为1000。

2.4 实验结果

根据实验测试，进行一次优化所需的时间旁瓣水平∶能量覆盖率∶平均方差≈100∶1∶150。由于能量覆盖率的计算速度最快，在一定时间内可以对能量覆盖率进行更多次的优化，其优化更为充分，可能更接近于最优。实验中对以能量覆盖率为目标的优化进程如图3。

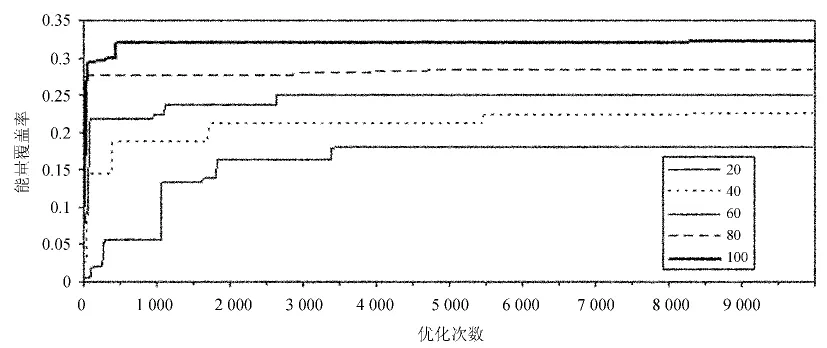
图3 阵列优化的进程示意图Fig.3 Course of the optimization experiment

图3分别列举了20、40、60、80和100个阵元情况下以能量覆盖率为目标的优化进程，可以看到在优化刚开始时优化进展较快，后期趋于缓和，并且阵元数目较多的情况始终保持着比更少阵元的较高能量覆盖率水平。从另外一个角度，展示了整个优化过程的情况(图4)。

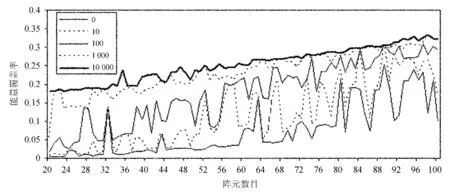
图4 阵列优化进程示意图Fig.4 Course of the optimization experiment showing progress over number of array elements

图4展示的是在100个阵元情况下的优化开始前和分别进行10、100、1000、10000次优化的各种阵元数目情况下的能量覆盖率水平。可以看到在优化刚开始时，不同阵元间的差别较大，优化到1000、10000以后，不同阵元的差别趋于稳定增长的水平。给出了实验的进程之后，最后给出实验得到的阵元数目分别与旁瓣水平、能量覆盖率和平均方差的对应关系(图5)。

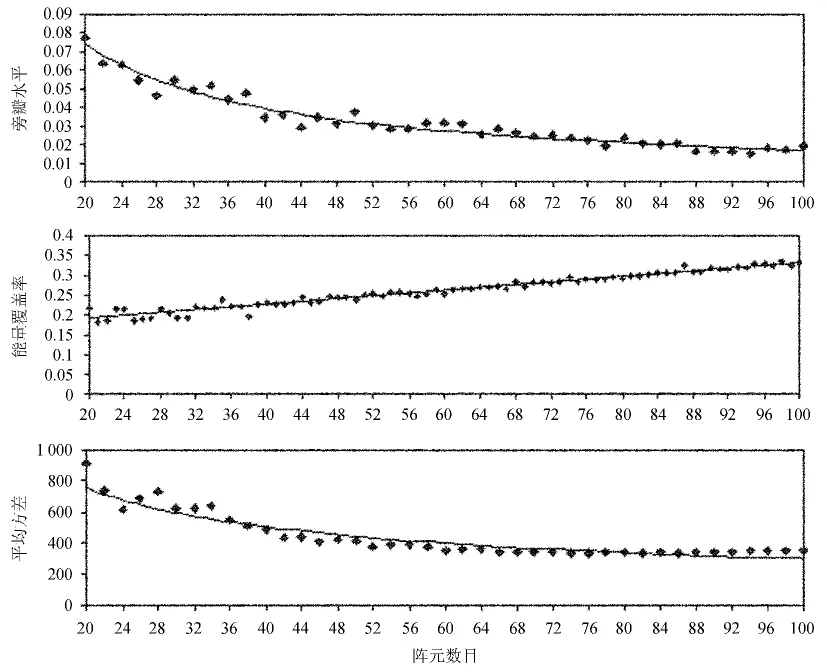
图5 各种评价标准与阵元数目的对应关系示意图Fig.5 Relation between each evaluation criterion and number of array elements

图5中的圆点均为实验数据，曲线为拟合曲线。其中旁瓣水平和平均方差使用幂函数进行拟合，拟合曲线的函数关系式分别为 y=1.129 1x－0.909和 y=4 160.8x－0.5717。能量覆盖率用一次函数进行拟合，解析式为y=0.001 8x+0.155 6。函数定义域均为［20，100］，在定义域内可以认为拟合函数具有较好的准确性。

3 结果利用

有了评价标准与天线数目的关系曲线，如何确定具体该建设多少个天线，总结起来可以有如下3类方法:

(1)成本截断。假定成本固定或者有严格上限，由于无论使用何种评价指标，天线数目的增加总意味着干涉阵列性能的提高，所以在成本允许的情况下，需要尽量建设较多的天线。在此基础上根据各方面的成本计算，最后可以得出最多可建设的天线数目。成本截断的方法必然要配合成本的估计和计算进行，对成本的估算也是一个非常复杂的问题。

(2)效果截断。这种方法假定成本在某一范围内可以接受，用效果作为截断的依据，一旦达到某个预定的效果，则可以作为天线的数目。效果截断的依据使用主观评价的结果，主观评价的一种划分标准为［11］:①好的——可供观赏的高质量的图像，干扰并不令人讨厌;②可通过的——图像质量可以接受，干扰不讨厌;③ 边缘的——图像质量较低，希望能加以改善，干扰有些讨厌;④ 劣等的——图像质量很差，尚能观看，干扰显著令人讨厌;⑤ 不能用的——图像质量非常差，无法观看。使用主观评价实验可以得出每个主观标准与各种客观评价方法的对应关系(表2)。

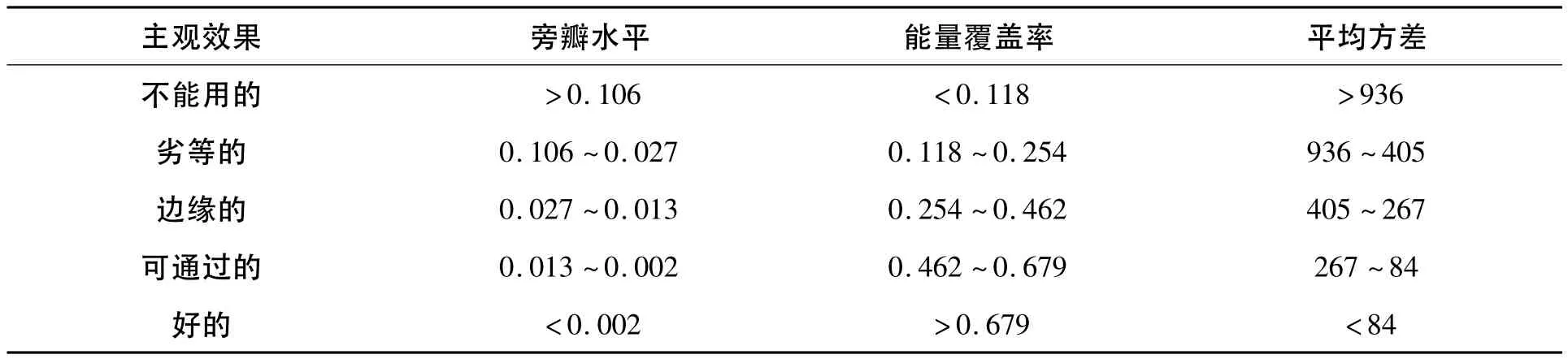
表2 主观效果与各种评价标准的对应关系Table2 Various evaluation criteria for subjective judgements

由于在射电波段的综合孔径成像是一个复杂的问题，所以不能寄希望于生成绝对高质量的图像，达到第3级效果的阵列已经可以满意，根据这3条标准在实验结果中进行截断，在3种评价标准下建议天线数目分别为61、59、55。

(3)其他方法。除了以上两种方法之外可以使用综合的方法，如增加阵元效率(Increasing Array Element Efficiency，IAEE)、性能价格比(Price-Performance Ratio)等，也可以考虑进一步将问题转换成一个基于更多约束条件的多目标优化问题。以平均方差为目标的增加阵元效率为例进行讨论，设平均方差与天线数目的对应关系RMSE=f(x)，则增加阵元效率定义为在当前阵元数目的基础上再增加天线带来的单位性能受益，即LAEE=f'(x)。根据前面的拟合结果可以得到以平均方差为标准的增加阵元效率LAEE=－2 378.7x－1.5717，表3列出了该函数的部分取值。

表3 不同阵元数目下的增加阵元效率Table 3 IAEE for different numbers of array elements

可以看到当阵元数目达到90后，再增加天线带来的性能提升仅为20个阵元时的不足9.4%，而当阵元数目为50、60时其性能提升约为20个阵元时的23.7%、17.5%，结合效果截断的结果认为建设50～60个天线作为阵元共同组成太阳低频射电阵列是较为合理的选择。

4 结论

在许多关于阵列设计的研究中将组成阵列的阵元数目作为已知或一个预设，然后在此基础上展开对干涉阵列的设计、优化等工作。本文将阵列数目作为一个待定的问题进行讨论，通过一定的实验和分析得出较为合理的阵元数目建议。首先通过遗传优化算法分别得出3种评价标准与天线数目的对应关系，然后利用截断和计算的方法对阵元数目给出推荐值。按照本文的实验结果和讨论认为太阳低频阵列建设50～60个天线是比较合理的阵元数目候选范围，如果受成本限制较多则考虑建设50个左右天线组成阵列，如果需要适当提高性能则可以增加至60个或更多，具体进行建设的准确数字要根据成本、建设地点等更多实际情况最终确定。

［1］Kogan L.Optimization of an array configuration minimizing side lobes ［J］.MMA Memo，1997，171.

［2］Boone F.Interferometer array design:optimizing the location of the antenna pads ［J］.Astronomy and Astrophysics，2001，377(1):368 －376.

［3］Su Yan.A new method for optimizing the configuration of the chinese square kilometer array［J］.Chinese Journal of Astronomy and Astrophysics，2004，4(2):198 －204.

［4］J Pety，F Geuth，S Guilloteau.ALMA+ACA simulation results ［J］.ALMA Memo，2001，387.

［5］吴胜殷，甘恒谦，张海燕.孔径阵列技术及其在射电天文中的应用 ［J］.天文学进展，2008，26(3):203－213.Wu Shengyin，Gan Hengqian，Zhang Haiyan.The AAT technique and its application in radio astronomy ［J］.Progress in Astronomy，2008，26(3):203－213.

［6］王威，颜毅华，张坚，等.CSRH阵列设计研究及馈源设计的初步考虑 ［J］.天文研究与技术——国家天文台台刊，2006，3(2):128－134.Wang Wei，Yan Yihua，Zhang Jian，et al.Array configuration and feed design for CSRH ［J］.Astronomical Research ＆ Technology——Publications of National Astronomical Observatories of China，2006，3(2):128－134.

［7］张仙玲，裴晓芳，陶纯堪.UV覆盖优化标准的初步研究 ［J］.南京晓庄学院学报，2006，22(4):27－30.Zhang Xianling，Pei Xiaofang，Tao Chunkan.The preliminary study on UV coverage optimizing criterion ［J］.Journal of Nanjing Xiaozhuang University，2006，22(4):27－30.

［8］Stephan Wenger，Soheil Darabi，Pradeep Sen，et al.Compressed sensing for aperture synthesis imaging［C］//Proceedings of international conference on image processing(ICIP)，2010:1381－1384.

［9］周景超，戴汝为，肖柏华.图像质量评价研究综述 ［J］.计算机科学，2008，35(7):1－4.Zhou Jingchao，Dai Ruwei，Xiao Baihua.Overview of image quality assessment research ［J］.Computer Science，2008，35(7):1－4.

［10］Zhou Wang.Modern image quality assessment［M］.Morgan ＆ Claypool，2006.

［11］庞建新.图像质量客观评价的研究 ［D］.合肥:中国科学技术大学，2008.Pang Jianxin.Research on image objective quality assessment［D］.Hefei:University of Science and Technology of China，2008.

［12］陈霄.DNA遗传算法及应用研究 ［D］.杭州:浙江大学，2010.Chen Xiao.Research on DNA genetic algorithms and applications［D］.Hangzhou:Zhejiang University，2010.