基于飞行训练的航空安全风险模糊评估方法

胡 杰

（中国民航飞行学院，广汉 618307）

0 引言

安全风险评估是指对某一特定系统所处安全运行状况进行的安全风险定性或定量化分析，它是制定安全策略，开展安全管理工作的前提和基础。评估方法的准确性和合理性，将直接影响到安全策略和安全工作的效果。可以这么讲，一种科学恰当的安全风险评估方法就是系统实施正确安全策略，实现安全风险控制最优化的开始。

民航系统，历来都高度重视安全运行管理工作，将安全视为生存和发展的生命线。在运行实际中注重安全管理体系建设，强调预防为主，防控结合的安全管理方式，并取得骄人业绩。但是，不管是传统的安全管理方法，还是目前先进的SMS(安全管理体系)，都没有很好地解决安全管理的核心问题-安全风险的准确评估。主要原因在于安全本身就是一个多元构成的复杂体系，具有一定的模糊性和不确定性。如果我们简单地以一个数字作为界限来硬性区分安全状况，一方面由于评估指标单一、评估方法不全面，不能准确反映出系统的实际安全运行状况；另一方面由于没有充分考虑系统安全的模糊性和不确定性影响，难以有效评估分析出安全运行状况的发展趋势。而这两个问题，都是安全风险评估中必须解决的问题。针对以上问题，如果我们引入一种综合评估程度较高，能有效解决模糊和不确定性对象的定性和定量的方法——模糊综合评价法，利用模糊数学的原理分析和隶属度理论，就能很好地解决上述两个问题。

1 安全风险评估模型的建立

1.1 安全风险评估的基本要素

利用模糊数学理论进行安全风险评估时，首先我们要确定安全风险评估要素。本文结合实际，以中国民航飞行学院安全评估需求为例，进行安全风险评估模型确定：作为一所以培养民航飞行员为主的院校，中国民航飞行学院拥有200余架飞机，每年培训飞行学生上千人，年度飞行训练时数超过20万小时，在飞行训练中，安全的主要威胁来自于组织指挥、飞行技术、航行管制、机群可靠性和运行环境变化等方面可能存在的漏洞；安全威胁的后果就是上述漏洞风险对系统造成的人员和财产损失的可能性；损失程度由安全漏洞、安全威胁度和系统安全可靠度共同决定。从安全风险评估的角度看，人员财产受损程度、安全漏洞和安全可靠度就是安全风险评估时必须考虑的三个要素。三者相互关联，互为影响。因此，系统的安全风险评估过程，就是安全漏洞、安全可靠性和人员财产损失度的确定过程。

1.2 安全风险评估要素的确定

由于逻辑与计算是乘积的运算，因此我们在安全风险评估数学模型中采用乘积计算模式，即安全风险=（安全漏洞×系统可靠度×安全威胁度），其中安全漏洞、系统可靠度、人员财产损失度可根据运行实测数据，与某一阶段训练飞行时间、起落架次、培训学生数量加权比较确定（如当某一阶段发生了一起飞行事故征候，安全漏洞数值我们可以使用安全威胁度×事件次数/飞行小时数进行确定）；其中安全威胁度的取值可根据民航局公布的不安全事件等级进行确定，具体如表1所示。

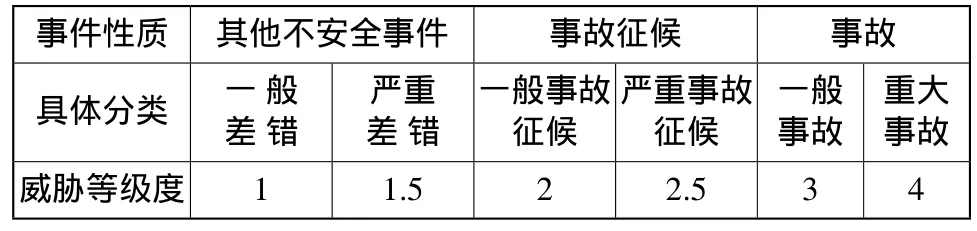
表1 安全威胁度值

2 评估方法

在评估模型中，主要借鉴了模糊数学原理和分析方法中比较重要的部分——隶属度概念，一方面解决了具有模糊性和不确定性对象的综合评估问题，另一方面实现了模糊性问题的定性、定量化计算，较为简单地得到一个用户容易接受，比较直观的评估结果，从而为制定安全策略，开展安全运行管理提供了理论基础。

2.1 隶属函数的确定

在模糊数学中，常常运用隶属度来刻画客观事物中存在的大量模糊界限，隶属度可用隶属函数进行表达，我们以表2为例进行说明。

表2 风险等级划分

当系统在某阶段运行安全风险值评估为25，按照风险评估表设定，我们可以判定系统处于中度风险区域，但安全趋势发展如何，下一步该采取何种策略，从上是不能得到更多信息的。如果我们运用模糊数学概念，用隶属度来进行刻画，就比较容易解决这个问题了。对上面的问题，我们可以利用隶属函数来确定，认为当系统安全风险值为25时，隶属中等风险级别程度为70%，隶属低风险级别程度为20%。隶属高风险级别程度为10%。此时，管理层对针对何处薄弱环节、采取何种安全对策一目了然。

2.2 建立关系模糊矩阵

在进行安全风险评估时，首先，我们将对构成安全风险的各个单项指标进行分别评价。假设取安全风险U为各项指标的集合，即U=(安全漏洞，安全可靠度，财产损失度)；取V为安全风险级别集合，即V＝(低，较低，中，较高，高),对U上单项指标进行综合评价，通过隶属函数分别求出各单项指标对应V上五个风险级别的隶属度，可以分别得到一组五个数。这样，最后可组成一个5×3的模糊矩阵，记住关系模糊矩阵R。

2.3 建立安全风险权重矩阵

一般来说，不安全事件等级越高，安全风险级别和威胁程度就越高，对系统的安全风险评估综合影响也越大，因此权重设定应该越大。假设构成安全风险的每个单项指标权重值为bi，可得到一个权重模糊矩阵B，记作B＝（b1，b2，b3）。

2.4 安全风险评估的模糊算法

经过单项指标综合评价并配以权重后，可以得两个模糊关系矩阵，即关系模糊矩阵R和权重模糊矩阵B。则综合安全风险评估模型Y＝B×R,其中Y代表模糊综合评估结果，是个1×5的矩阵，即Y ＝（y1，y2，y3，y4，y5)，其中 yi代表最后安全风险综合评估结果隶属第i个安全风险级别的程度。

如果我们需要对最终评估结果进行量化，可以通过函数定义来实现。比如我们定义N＝Y1×1+Y2×2+Y3×3+Y4×4+Y5×5 即 可 量 化，N即是综合安全风险评估数值。

3 安全风险模糊评估方法的具体应用

下面我们以民航飞行学院2010年运行状况安全风险评估来说明基于模糊数学的安全风险评估模型在实际中的应用。

首先通过对2010年发生的航空不安全事件次数、性质进行分析，对比事件安全威胁程度，同时与2010年年度训练飞行时数、年度飞行起落架次和培训飞行学员数量进行综合衡量，我们得出2010年民航飞行学院系统安全漏洞、安全可靠度、人员财产损失度三项指标评估结果分别对应的安全风险级别为：3,2,1。那么，根据隶属函数的定义，各个单项指标隶属各个风险级别的隶属度如表3所示。

因此，我们可得到关系模糊矩阵为

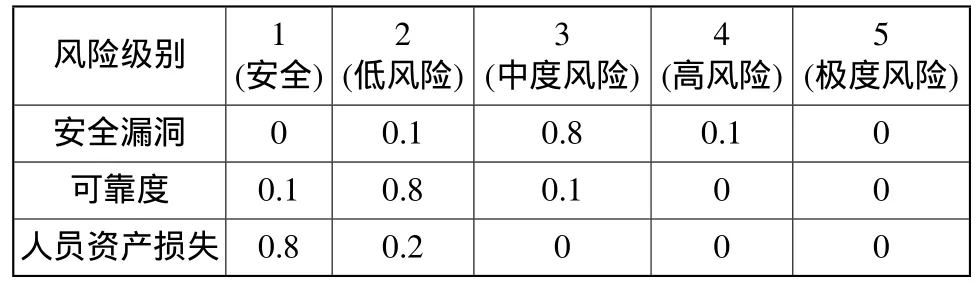
表3 风险级别

按照风险大小，对上述单项指标进行权重确定，取b1＝0.3，b2＝0.3，b3＝0.2，那么权重模糊矩阵为（0.3,0.3,0.2）；

所以，

因此，得到的评估结果隶属各个风险等级的概率如表4所示。

4 结束语

通过以上分析，我们可以清楚看出2010年民航飞行学院安全运行状况隶属各个风险等级的程度：安全风险主要集中分布在低、中两个区域。在后期管理中，如果我们针对评估中发现的薄弱环节采取有效措施，安全风险将能得到有效控制，安全形势将向更有利方向发展。

表4 各风险等级的概率

最后我们可以对上述评估结果进行量化计算，得出风险的评估值为：

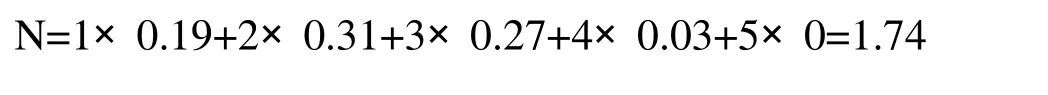
[1]李敬,曹义华.中国民航安全评价方法研究[J].中国安全生产科学技术，2008,10.

[2]石丽娜,周慧艳,汪洋.基于5S训练模式的航空安全管理[J].中国民航飞行学院学报,2008,3.

[3]刘汉辉.科学管理与飞行安全[J].中国民航飞行安全技术,1995.10.