MATLAB在模拟煤层气扩散中的应用
马 胜,虞青松
MATLAB在模拟煤层气扩散中的应用
马 胜,虞青松
(中国矿业大学资源与地球科学学院,江苏 徐州 221008)
根据质量守恒原理推导的煤层气在煤储层中扩散运移方程(菲克第二定律),由于求解方法复杂,计算工作量大,在实际的运用中受到限制。而通过数学软件Matlab中的偏微分方程求解器PDETOOL GUI(pedtool),可以形象直观的模拟煤层中的煤层气在储层中扩散与分布。现以宁武煤田太原组4号为例,模拟结果表明,煤层气浓度扩散与实际具有较好的吻合特征。
质量守恒;菲克定律;数值模拟;MATLAB
根据分子运动理论,扩散过程是分子的自由运动使得物质由高浓度体系到低浓度体系的一种浓度平衡过程,气体浓度梯度是推动力[1],Smith和Williams认为煤层气在煤粒孔隙扩散遵从菲克(Fick)第二定律既非稳态扩散[1],非稳态扩散模式中,主要有两点:一是认为煤基质块内甲烷浓度从中心到边缘是变化的,且中心点的浓度变化率为零;二是基质边缘处浓度是煤储层压力控制的等温吸附浓度,随着煤层气不断开采,煤基质块的浓度随之变化。非稳态扩散模型能客观地表示煤基质块中的煤层气浓度时间与空间变化,能反映煤层气的扩散过程,但缺点是计算复杂,工作量大。而数学模拟软件Matlab中偏微分方程求解器PDETOOL GUI(pedtool)可以方便的模拟解算。
1 煤基质微孔隙扩散方程
建立如图1所示的微元体,其参与扩散的是吸附状态煤层气C;分别为质量扩散通量矢量m在三个坐标轴方向分量;对孔q是单位时间质量交换;t为时间,根据质量守恒原理,各轴向上单位时间扩散流入微元体质量减去流出质量,再加上质量源生成量等于单位时间质量变化量[2]。
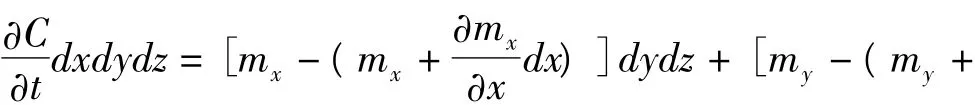
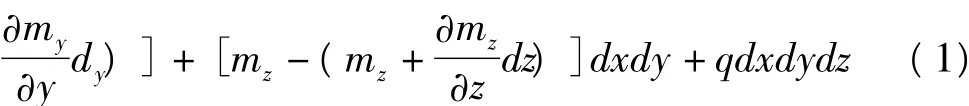

图1 孔隙系统中微元体的质量守恒
整理得扩散的连续运动方程为:

由Fick扩散定律进行扩散定律:
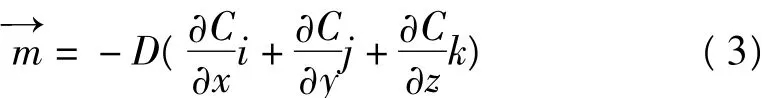
将Fick定律方程(3)代入扩散连续方程(2)中,得到孔隙系统中吸附状态煤层气扩散运动微分方程:

式中:
C—浓度,kg/m3;
t—时间,s;
q—单位时间交换质量,kg/(m3·s);
D—扩散系数,m2/s。
2 模拟实列
2.1 地质概况
宁武煤田地处山西地区北中部,煤田南北长,东西窄,呈北东向斜列,展布于鄂尔多斯地台,吕梁地块、五台地块及内蒙地轴之间为一继承性上叠构造盆地,从总体看来,构造复杂程度尚属简单类型。本区含煤地层为二叠系下统山西组、石炭系上统太原组、中统本溪组,主要可采煤层为太原组4,6,9号煤层,现以4号煤层为例,该煤层厚度为1.55~10.55 m,平均为4.07 m,顶底板岩性为砂质泥岩、中粗砂岩,炭质泥岩、粉细砂岩,砂质泥岩。煤层结构简单,稳定性较好,分叉区内除西—西北部边界局部风化外,其余全区可采。煤层的参数为密度均为2.5 g/cm3,扩散系数为2.5×10-8,扩散通道厚度为20 m,初始含气量30 cm3/t,扩散通道和储层的初始甲烷浓度均为0;模拟100 Ma之后,储层的甲烷含量。
2.2 求解过程
打开PDE TOOLBOOKSGUI窗口,在应用模型中选择 generic scalar,由条件可知边界满足齐次Dirichlet边界条件,在PDE Mode模式下,分别双击3个区域设置抛物型(paraboli),因为要求的解随时间变化的PDE,故需要定义初始值和时间间隔,打开Solve Parameters对话框,需输入时间向量 logspace(1,8,10),初始时间是 10,选择 Mesh 网格划分,在选择Refine Mesh命令加密的三角网格的划分,最后再选择Jiggle Mesh优化网格的划分。
2.3 数值模拟的结果
在Plot Selection命令中选择Color(颜色),Contour(等值线),Arrows(方向),Height(3 -D plot)(三维图像)Show mesh(显示网格)等选项,也可以选择动态模拟的结果,可以在对话框中选择animation(动态模拟),最后再点击Plot选项(图2)。
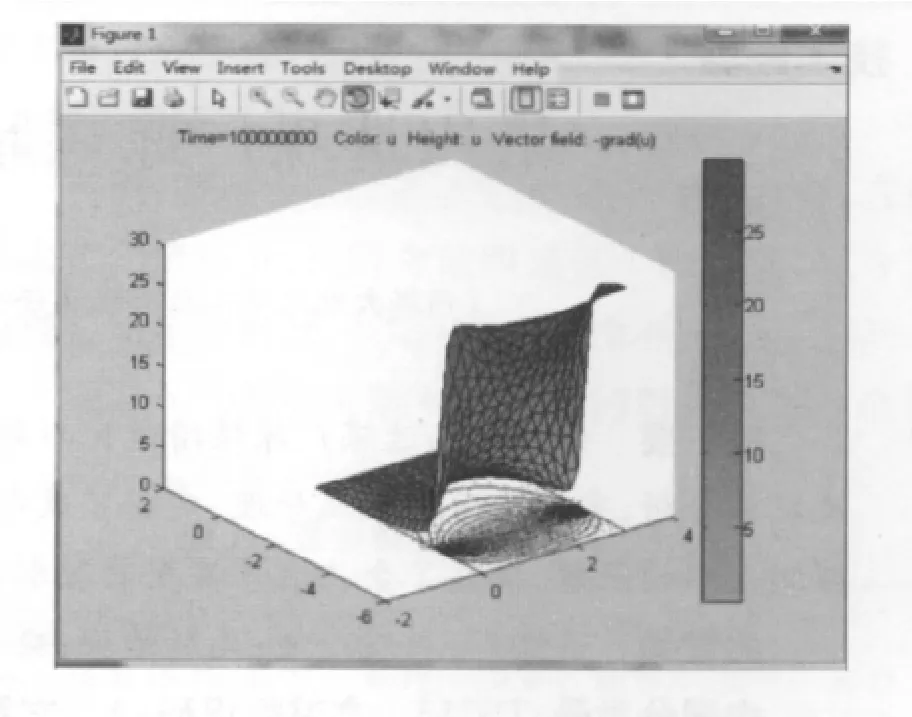
图2 数值模拟的结果图
从图2可以看出,模拟的结果和实际情况具有较好的吻合特征,且随着时间的推移煤层气在煤层中的扩散是逐渐向上运移,煤层的顶板的气体浓度要比煤层的地板的高这符合实际的情况,非平衡扩散模型模拟(Fick第二定律)表明甲烷浓度的减小是不断的向远方传递的,从煤层的浓度等高线看出煤层的中部浓度梯度的变化比较大。
3 结论
1)由于大部分的煤层渗透率比较低,低流速低渗透率下流体的渗流规律,达西公式(dracy)可能就不再适用,但是煤层气在煤粒孔隙中的扩散规律比较符合菲克(Fick)扩散定律。
2)Fick方程虽然是抛物线型方程具体的求解过程比较复杂,经常没有具体的解析解,但是运用matlab中的PDETOOL求解器来解方便简单,而且可视化的效果比较好,还可以生成解的动画,这些操作通过命令行都很容易实现。
3)通过对所建的拟稳态非平衡吸附煤层甲烷运移数学模型进行模拟,模拟结果表明,煤层气浓度扩散与实际情况具有较好的吻合特征,数值模拟的结果能用于科研并为生产实践提供参考预测。
[1] 吴世跃.煤层气与煤层祸合运动理论及其应用的研究具有吸附作用的气固耦合理论[M].北京:科学出版社,2009:103-105.
[2] 周世宁,林柏泉.煤层瓦斯赋存与流动理论[M].北京:煤炭工业出版社,1999:79-81.
[3] 骆祖江,张 珍.水气二相渗流祸合模型及其应用[J].水文地质工程地质,2004,3(1):51-54.
[4] 吴 鹏.偏微分方程的matlab的算解[M].北京:高等教育出版社,2002:157-159.
[5] 成绥民,成 珍,杨勤涛.气一水两相渗流稳定与不稳定试井分析[J].油气井测试,2006,15(3):4-8.
Application of MATLAB in Simulation Coalbed Methane(CBM)Diffusion
Ma Sheng,Yu Qing-song
According to the principle of conservation of quality is CBM reservoir in coal of diffusion migration equations(fick's second law),with the methods of solving are complex,computing workload are large,in actual use was limited.And through the mathematical software Matlab partial differential equations of the PDETOOL GUI(pedtool),can be very intuitive simulation of coal seam image CBM reservoirs in the diffusion and distribution.Now Ningwu coalfield Taiyuan group No.4 as an example,simulation results show that the concentration of coalbed methane(CBM)diffusion and it actually has a better agreement characteristics.
Conservation of mass;Fick law;Numerical simulation;MATLAB
[TD12]
A
1672-0652(2012)01-0044-02
2011-12-05
马 胜(1983—),男,新疆巴州库尔勒人,2010级中国矿业大学在读硕士研究生,主要从事矿产普查与勘探的研究(E -mail)masheng1983@126.com

