学生物理解题思维能力的提高

魏 华

(北京四中 北京 100034)

提高解题能力，不仅仅是应试的需要，也是素质提高的需要．在教学中，笔者一直思索着学生解题中有哪些问题，以及如何提高解题能力．有一点体会，陈述如下.

1 学生解题中存在的问题

(1)读完题，不知所云者．此类学生大多数知识上存在着严重漏洞，或者是阅读、理解字面意思能力较差，也不排除建立物理图景能力极差．

(2)只会套公式者．此类学生进入了一个误区，认为解物理题就是套公式．不管三七二十一，找到一个数据，一套完事，解完后自己都不知干了什么，往往即使出现极不合常理的数据也不知道．或仅能解出一小步，如某些动量综合问题，只会应用动量守恒求出某速度，而不会继续往下探究．他们的解题是“机械的”，也是一种定势思维．

(3)思维片面者．此类学生表面看一般思维较敏捷，一会儿就出结论，但仔细一问，往往思维简单，看问题片面，且漏洞百出．

(4)信心不足者．此类学生缺乏克服困难的信心，面对过程稍微复杂或计算较繁琐的问题，常有畏难情绪，没开始解题就已矮了半截，表现为，解题往往只能半途而废．

总结上述各类情况，可以看出，“扎实知识+思维能力+坚强意志”是解题的三个最重要因素．笔者认为，其中最关键的就是思维能力的培养．

2 解题思维能力的培养

2.1 确定分析什么——状态加过程

如同了解一个人，我们首先得知道他现在的状态，还得清楚他的过去，尤其得清楚他达到现在这种状态，是经历了一个怎样的过程，这样我们才能全面地了解他．解题也一样，确切清楚状态和过程，就可以将问题很好解决．如：“用绳子拉着质量为m的小球，在竖直面内做完整圆运动，求在最低点的拉力最小值？”

状态：在最低点，由牛顿第二定律

(1)

当在最低点的速度最小时，则拉力T最小．那最低点速度怎么来的呢？往前追述.

状态：在最高点，由牛顿第二定律

(2)

要通过最高点，则T′等于零时，则此时

连接这两个状态的是一个怎样的过程呢？从能量角度，有机械能守恒．则有过程：由最高点到最低点，由机械能守恒得

(3)

状态(1)+状态(2)+过程(3)式，问题得解．一般物理问题的设置及解决都离不开状态和过程的分析．

2.2 研究解题是什么——解题等于描述

笔者认为，解题其实就是一个从不同角度对物理过程进行描述的过程．

(1)用语言、文字描述物理过程

答疑时学生问老师一个题，我们常会反问：“你把这个过程说说看!”于是学生“磕磕绊绊”地说着，“物体先……，再……，然后……”说着说着，学生突然一拍脑门，“噢，忘了，……，会了”．于是学生特别佩服老师——不说话，就把问题给解决了．其实我们心里特别清楚，很多学生题解错，就是因为做题前总急于动笔算，总想不起来要去分析过程，于是我们让他“说说看”，让他补上这一环节，好多问题就在“说说”的过程中被解决．

这也是改正“只会套公式”的最有效的一步．他总以为解物理题就像做数学一样，总想代公式．我们就偏让他每做题前想想，说说怎么回事，慢慢地，他也就习惯了这种解决问题的方式，“套”公式前，会琢磨琢磨什么物理情景，这就为彻底解决问题提供可能．

(2)用图景描述物理过程

物理图景的正确建立应是我们在物理教学中总要强调和追求的东西．问学生什么是物理，他想起的应该更多的是一个个生动的画面，小车往前运动，小球在空中运动等，而不是一个个简单的公式．要能做到这一点，需要我们在平常教学时，能演示的演示，能用简笔画图说明的画图说明，让学生接受并学会这种描述过程的方式．解题时，要总想着画个简图，表示出这个过程．这样做可以将物理过程具体化，有助理解过程；画图时，不自觉地从题中将重要信息提取出来，有利解题．

举个例子说明：先用F1将物体由静止拉动时间t，然后撤去F1，同时施以反向的F2作用，又经过时间t，物体回原处，这个过程，用语言描述就是：物体先在F1作用下，做匀加速运动，后在F2作用下，会先减速到零，再反向匀加速运动，直至回到原处．用简图描述一下.

做出图1，很快会理解该过程，并能提炼出两段过程时间相同，位移大小相等的条件，则平均速度大小相等，可解．

图1

(3)用已知定理定律描述过程

这是很实质性的一步，是要将你的思维过程，用数学工具展现出来，并求出某个物理量．结合刚才谈到的“状态+过程”的问题，笔者认为，做好这一步，最重要是搞清楚用什么定理定律去描述一个状态和一个过程．

对于状态，笔者以为，高中物理力学中，一般就是利用牛顿定律进行描述，如上述对圆周运动例子中的在最高点和最低点的描述，就是利用牛顿第二定律．

对于过程，则主要有三个工具可以描述：一为匀变速运动公式，主要适用于单个物体做匀变速运动；二为能量，适用范围较广，主要是利用动能定理、能量守恒进行描述；三为为动量守恒定律，适用于两个或以上物体相互作用过程时．

借助一个例子，将以上三种描述方式，进行阐述．

【例1】质量为M的机车拉着质量为m的拖车，在平直的轨道上匀速前进，拖车中途脱钩．当司机发现时，机车已离脱钩处有L距离，于是立即关闭油门撤去牵引力．设机车的牵引力是定值，机车和拖车受到的阻力都与车重成正比．求机车和拖车完全停止时相距多远．

解析：过程Ⅰ脱钩后，拖车做减速运动，机车加速；过程Ⅱ当司机发现并制动机车后，机车减速，可能在此过程中，拖车减速至零．

用一简图画出该过程，如图2.

图2

方法一：设牵引力F，所受的阻力

f=k(M+m)g

由开始时是匀速前进

F=f=k(M+m)g

脱钩后，机车根据牛顿第二定律

F-kMg=Ma1

状态式

机车加速，位移为L，设初速度为v0，则在L处的速度

v12-v02=2a1L

过程式

刹车后，根据牛顿第二定律

kMg=Ma2

状态式

设总位移为s1，有

-2a2(s1-L)=-v12

过程式

对于拖车，根据牛顿第二定律

kmg=ma3

状态式

减速至零，有

v02=2a3s2

过程式

联立求解以上各式，得到

以上就是利用牛顿第二定律(状态)+匀变速运动公式(过程)求解得到．

方法二：用能量来描述过程

对于机车，由动能定理

WF+Wf=ΔEk

即

过程式

对于拖车，由动能定理

Wf′=ΔEk′

即

过程式

F=K(M+m)g

解以上各式可得

方法三：若在描述过程中注意到，若绳断时，机车也马上刹车，则两者停在一处，而由于由牵引力F多做功FL，所以机车比拖车多行了d，摩擦力多做了KMgd的功.则由以上分析可知

FL=KMgd

所以

可见，这三个角度的描述，在解题时有机结合在一起，问题就会很易于理解，易于解决．

(4)用图像来描述过程

举个例子来说明：

【例2】如图3所示，一个铁球从竖立在地面上的轻弹簧正上方某处自由落下，接触弹簧后将弹簧压缩．在压缩的全过程中，弹簧的压缩量最大时

A．球所受合力最大，但不一定大于重力值

B．球的加速度最大，且一定大于重力加速度值

C．球的加速度最大，有可能小于重力加速度值

D．球所受弹力最大，且一定大于重力值

图3

解析：(1)语言、文字描述.球下落的过程，先做自由落体运动；与弹簧接触后，弹簧弹力由零逐渐增大，小球做加速度变小的加速运动；当弹簧弹力等于重力时，小球加速度为零，速度达到最大；继续向下运动，则弹簧弹力会大于重力，做加速度增大的减速运动；当减到零时，弹簧压缩量最大．

(2)v-t图像描述.如图4，在速度为零时，小球的加速度(即图像的斜率)一定大于g；则选B，D．

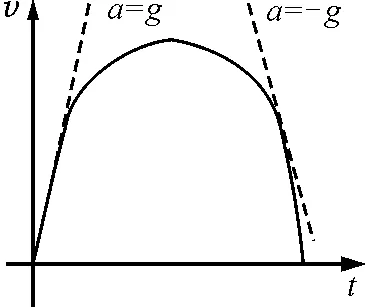
图4

运用图像来描述过程，是一种无国界的语言，它能直观、简明地将物理过程表现出来．对于v-t图像，只需遵循斜率表示加速度，面积表示位移这两点，一定能很好做出．所以笔者总强调学生对于复杂运动，或加速度变化的运动过程，都要试着用v-t图像去描述一下，即使不能用之来解题，也一定可以用其帮助理解过程．因为它本身就是思维的产物．

3 实践中的体会

在平常习题教学中，笔者一直坚持从上述各角度来描述物理过程，觉得有以下几点收获．

(1)将解题等效为描述题，降低了解题的心理门槛．这并不是简单地改变了一种说法，在实际操作中，学生遇到题知道如何入手了．乍一看，不会的问题，在“说着说着，画着画着”的过程中就会找到思路，从而解出问题；

(2)形成良好解题思维习惯．每道题，都坚持这样去做，久而久之，学生耳濡目染，也会养成下笔解题前先分析过程，再考虑应用什么定理定律来解决的良好解题习惯；

(3)使学生解决问题信心增加．信心的增加，离不开成功的经验，成功的次数越多，信心越大．教学时，大部分时间，笔者会让他自己说，自己画，自己写，而笔者只在旁边指导：该说了，该画了，该挑公式描述了．偶而改正一下他的错误观点，所以学生很有成就感，自然，信心也会倍增．

解题思维的训练、能力的提高，是笔者教学中一直思考的问题．解题能力也是素质教育中的一个重要部分，尤其在应试向素质教育转轨期，更应该研究如何有效地提高学生解题能力．以上对于学生良好思维习惯的形成，在实践中，还是很有成效的．对于学生如何更好地创造性解题、更好地发散，是将要进一步研究的课题．