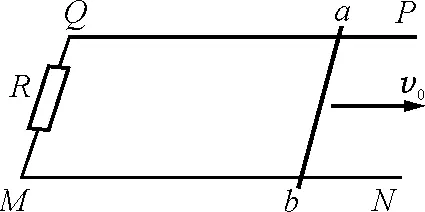匀变速直线运动中基本题型的分析与求解
谢国兴
(江苏沛县中学 江苏 徐州 221600)
1 运动性质的判定及初速度的确定
当题目中给定物体做匀变速直线运动时,首先要明确运动的性质是匀加速还是匀减速.当运动性质不能确定时,必须要同时考虑匀加速和匀减速两种情况,其解必为两组.当运动性质确定后,若为匀加速,则必须考虑初速度,初速度为零仅仅是匀加速直线运动的一种特殊情况.
【例1】一个物体做匀变速直线运动,某时刻的速度大小为4 m/s,1 s后速度大小变为10 m/s,求在这1 s内加速度和位移的大小.
解析:该题并没有明确物体运动的性质,因此,必须同时考虑匀加速和匀减速运动两种情况.
匀加速运动

代入数据得
a1=6 m/s2
s1=7 m
匀减速运动
代入数据得
a2=-14 m/s2
s2=-3 m
2 初速度为零的先匀加速运动后匀减速运动至速度为零
该题型的切入点是抓住该过程中的最大速度即匀加速运动的末速度或匀减速运动的初速度,其方法是

(2)已知匀加速运动的加速度a1及位移x1和匀减速运动的加速度a2及位移x2时,可选用公式
a1x1=a2x2
已知匀加速运动的加速度a1及时间t1和匀减速运动的加速度a2及时间t2时,可选用公式
a1t1=a2t2
【例2】质点从A运动到B,已知初速度为零,从A到B间某点C的加速度为a1,方向与运动方向相同,从C点到B点加速度为a2,方向与运动方向相反,到达B点时速度恰好为零,AB=L.



D.AC∶CB=a1∶a2

本例已知加速度和位移,可选用公式vm2=2ax,即a1x1=a2x2,而x1,x2未知.
设AC段的位移为x1,CB段的位移为x2,那么x1∶x2=a2∶a1,选项D错误.
由
得
选项B,C正确,答案为选项B,C.
3 匀减速直线运动
解决该类问题的关键是首先要确定该运动是否具有往返性,若具有往返性,可把该过程分解为单方向的匀减速运动和反方向的匀加速运动两个分过程来处理.其解可能为一个,也可能为两个或三个,切不可漏解.

【例3】 一个以4 m/s为初速度做直线运动的物体,加速度的大小为2 m/s2,方向与初速度方向相反,问经过多长时间位移的大小为3 m?
解析:本例是一个具有往返性的匀减速运动,当给出位移大小时(注意大小两字),对应的时间可能有多个.
由
当位移为正时
3=4t-t2
得出
t1=1 st2=3 s
当位移为负时
-3=4t-t2
得出
本例中t3是学生最容易漏掉的一个解.
4 追及问题
通常涉及到的追及问题有,一个匀速运动和一个匀加速运动或一个匀速运动和一个匀减速运动的追及.处理该类问题的关键是(1)确定两运动物体开始计时的初始位置;(2) 分析两物体速度相同时的相对位置及以后运动状态的变化;(3) 注意未相遇前匀减速运动的物体是否已静止;(4)题目中是否存在二次相遇.
【例4】 如图1所示,甲、乙两辆汽车原来停在平直公路上的A,B两处,A,B间的距离为85 m.现甲车先开始向右做匀加速直线运动,加速度为a1=2.5 m/s2.甲车运动6 s时,乙车开始向右以加速度a2=5 m/s2做匀加速直线运动,求两车相遇时距A处的距离.

图1
解析:本例为两个匀加速运动物体的追及且起始点不同,起始运动时间也不同,因此,首先要判定乙车运动时,甲车与乙车的相对位置.乙车运动时,甲车走过的距离为s1,则
代入数据得
s1=45 m<85 m
因此,乙车运动时,甲车在乙车后40 m 处,即乙车开始计时两车位置差为s0=40 m.由于乙车的加速度大,当甲、乙两车速度相同时(关键点)如果甲车没有追上乙车,则两车不会相遇,两车速度相同时,乙车运动的时间为t,有
a2t=a1(t+t1)
t=6 s
此时,甲、乙两车的位移分别为


代入数据得
s甲=180 m
s乙=90 m
s甲-s乙>85 m
故两车速度相同时,甲车已追上并超过乙车,速度相同后乙车追甲车,必有两次相遇,设两车相遇时甲车用时t2,则
(起始点及起始时间均不同)
得出


由
代入数据得
s1=125 m
s2= 245 m
5 图像法求解
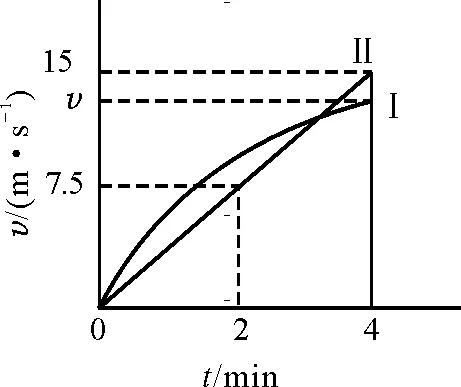
利用图像求解是研究匀变速直线运动的最显著特点之一,它的优点是直观、方便、省时、正确率高.但同时由于利用图像法求解要有很好的想象力和洞察力,并且这类题目往往具有一定的隐蔽性,所以学生在选择利用图像法求解中,通常会存在一定的困难.在什么情况下优先考虑图像法求解呢?(1)题目中作定性讨论,不作定量计算;(2)加速度未知;(3)有共同的物理量,如位移相同或速度相同等.
【例5】甲、乙同时由静止从A出发,沿直线AB运动,甲先以加速度a1做匀加速运动,经一段时间后改为以加速度a2做匀加速运动,到B时速度为v,运动时间为t甲;乙一直以加速度a 解析:本例符合图像法求解的要件,即题目要求作定性讨论,且加速度的大小未知,但位移和运动的末速度相同.因此,我们作出v-t图像如图2所示,时间t乙确定后,由a1>a,可作出甲运动的v-t图像有Ⅰ,Ⅱ,Ⅲ三条,由于运动位移(即图像面积)相同,甲实际运动的图像必须符合图线Ⅰ,故得出结论t甲 图2 所要指出的是,当物体的运动为非匀变速直线运动时,匀变速直线运动的公式不再适用(a变化).对题目中所涉及到的运动学的物理量的求解,我们通常采用的方法是“图像法”和“微元法”. 【例6】一辆汽车在恒定的功率牵引力下,在平直公路上由静止出发,经4 min的时间行驶 1.8 km.则在4 min末汽车的速度 A.等于7.5 m/s B.大于7.5 m/s C.等于15 m/s D.小于15 m/s 图3 由位移相同,作出辅助线Ⅱ,由图线可看出4 min时该点在实际速度的上方,即4 min末的速度小于15 m/s ,大于 7.5 m/s.答案为选项B,D. 【例7】如图4所示,光滑U型金属轨道PQMN水平固定在竖直向上的匀强磁场中,磁感应强度为B,导轨宽度为L,QM之间接有阻值为R的电阻,其余部分电阻不计.一质量为M,电阻为R的金属棒ab放在导轨上,给棒一个水平向右的初速度v0使之开始滑动,最后停在导轨上.求此过程中ab棒运动的位移. 图4 解析:由题意可求出ab棒运动的加速度 由于速度v变化,加速度a变化,因此,该过程是一个加速度不断减小的非匀变速过程,和图像法求解不同的是本例要求求出最终结果,因此必须要选择合理的公式求解,而本例中位移的求解实质上是一个求“和”的过程,这种情况下,我们优先考虑微元法.整个过程中,速度虽然在变化,但速度变化量的大小却是定值,即 Δv=v0 由运动学公式v=at对v进行求和 ∑v=∑at 其中 ∑v=Δv=v0 ∑vt=x 即ab的位移为