吹填土地基真空预压模型优化及参数设计
曹文昭, 郑俊杰,董佳竹
(华中科技大学 土木工程与力学学院, 湖北 武汉 430074)
随着我国沿海经济的发展和城市基础建设的蓬勃开展,沿海城市对土地的需求量日益增长,为缓减土地资源紧缺,适应城市发展的需要,填海造陆成为沿海城市拓展陆域面积的重要手段之一[1]。吹填土地基因其特殊的形成过程和组成成分,具有三高一低的典型特征,即天然含水量高、孔隙比大、压缩性高和抗剪强度低,一般呈软塑或流塑状态。为改善吹填土地基的工程性质,提高承载特性,降低吹填土地基的含水量是关键。
目前在实际工程中采用较多的是真空预压排水法,与传统的堆载预压法相比,真空预压排水法(以下简称真空预压法)具有工期短、成本低和加固效果好等优点[2~4],因此越来越多地被应用于围海造陆、港口以及高速公路等工程的软土地基处理中,特别是新吹填土等超软地基的加固处理。
砂井设计是真空预压法设计的重要组成之一,目前,在砂井地基设计和工程计算中仍采用基于轴对称固结“单井”假设的巴隆解析解,但实际上各相邻砂井相互影响,其对地基变形的作用效果是相互叠加的[5],即群井效应。为方便工程计算,现行规范[6]仍按照单向压缩分层总和法计算真空预压荷载作用下的地基最终竖向变形,再根据实测资料对计算结果进行修正,但实际上真空预压地基属于空间渗流、空间压缩,预压区周围的土体发生指向预压区的侧向变形。因此真空预压地基变形计算理论上还不成熟,而采用数值分析软件能较好地模拟真空预压过程中吹填土地基中孔隙水压力的变化规律及固结变形过程[3~5, 7, 8]。Indraratna等[8]结合修正Cam-clay理论,建立了同时考虑井阻和涂抹效应的解析方程,同时采用等效平面应变模型对路堤荷载作用下采用塑料排水板处理的软黏土地基变形进行了分析和预测;彭劼等[9]通过现场试验和数值计算发现加固区土体侧向位移具有先向加固区内、然后向加固区外移动的特点;朱继伟等[5]采用有限元程序研究了固结系数、排水板打设间距、真空度和预压面积等因素对真空预压处理地基侧向变形的影响;陈平山等[3]提出了将单井涂抹效应对涂抹区内土体渗透系数的弱化作用均化到单井影响区内土体的方法,有效减少了三维有限元计算的前处理工作量;孙立强等[4]提出在平面应变有限元分析中对吹填土体各节点施加有效自重以考虑真空预压前地基中存在的超孔隙水压力,以模拟插板期由于超孔隙水压力的消散引起的沉降。
上述研究主要分为考虑砂井固结的三维轴对称模型和考虑砂墙固结的平面应变模型,没有进行考虑砂墙固结的三维数值分析。本文借鉴砂井地基涂抹效应均化方法得到不考虑涂抹区尺寸的砂墙模型,对等效变换的有效性进行了研究,同时建立“多墙”三维有限差分模型,对真空预压处理吹填土地基效果和加固区面积的影响进行了研究。
1 砂井地基三维有限差分模型
1.1 真空荷载施加与真空度传递
将真空荷载施加在砂井或排水板侧壁上,由于井阻作用,真空度在砂井中沿地基土体深度方向传递的过程中必然存在一定的损失,从而使土层深部的真空度小于地表密封薄膜下的真空度。真空度在砂井内的传递与井料的颗粒组成和渗透性有关,赵常洲[10]通过现场试验对真空度在塑料排水板中沿深度方向的分布进行了研究,根据其研究成果,20 m深砂井中真空压力的分布可以近似简化为沿深度方向线性衰减,如图1所示。

图1 真空压力在砂井中的分布规律
1.2 涂抹区的处理
在吹填土地基中打设竖向排水体会对周围土体产生扰动,形成环状涂抹区,在涂抹区内,土体渗透性降低,压缩性增大,从而显著影响地基固结速度。传统竖井理论通过假定井周涂抹区的范围和渗透系数来反映涂抹效应对于地基固结的影响,JGJ 79-2002《建筑地基处理技术规范》建议涂抹区半径与竖井半径的比值为2.0~3.0,渗透系数为天然地基的1/5~1/3[6]。由于井周涂抹区范围较小,在大片砂井地基三维模型中反映涂抹区的几何尺寸与渗透系数很困难,计算成本也将大大提高,因此需要对涂抹区的建模进行适当简化。由于砂井地基固结以径向固结为主,陈平山等[3]根据固结度相等的原则,采用谢康和求得的等应变条件下砂井地基考虑井阻和涂抹作用径向排水固结的精确解[11],将涂抹效应对涂抹区内土体渗透系数的影响均化在井周rw~re范围内的土体中,其中rw为砂井半径,re为砂井影响区半径,此时无需将涂抹区的几何尺寸和渗透系数单独反映在三维模型上。
(1)
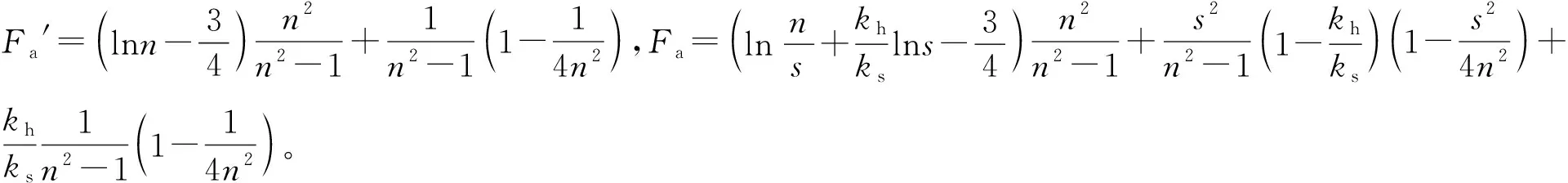
下面通过一算例来对上述方法进行验证。选取“单井”进行分析,建模参数为n=15,rw=7 cm,s=3.0,kh=4.0×10-7cm/s,kw=1.0×10-2cm/s,kh/ks=4.0,H=20 m,E=2.7 MPa,v=0.35,根据式(1),可得kh′=0.3809kh。根据对称性,取1/4单井采用FLAC3D软件进行建模,地下水位线位于地表平面,地表位移自由,为透水面;侧面及基底位移约束,为不透水面。对平均固结度进行分析,如图2所示。由图2可知固结10 d时平均固结度相差较大,之后迅速减小,固结40 d时,误差已小于5%,因此,该均化方法是可行的。
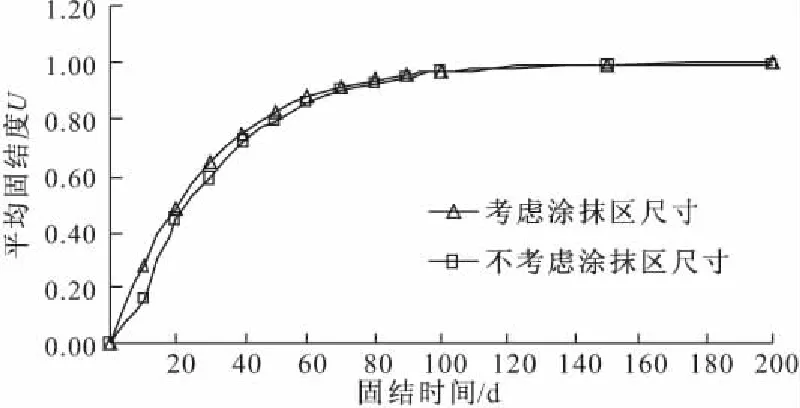
图2 涂抹效应对平均固结度的影响
2 砂井地基与砂墙地基的等效转换
在常规工程设计中,一般将砂井地基中砂井群简化为单井处理,按轴对称问题分析其固结过程。对砂井群地基进行数值建模分析时,由于砂井的分布具有密集、不连续和尺寸较小等特点,在三维模型中考虑所有砂井会导致单元划分过细,分析计算工作量大大增加,因此需要对砂井群地基进行等效简化处理。平面应变问题的数值建模与分析相对容易,可以将三维砂井地基转化为平面应变问题进行处理,基本思路是将按一定间隔与规律分布的砂井简化为连续分布的砂墙,如图3所示,简化后的砂墙地基既可以当作平面应变问题来分析,也可以取一定长度的砂墙进行三维建模分析。
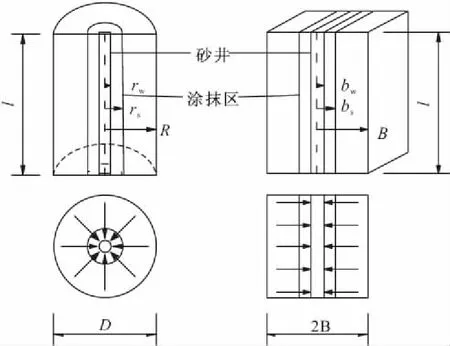
图3 砂井与砂墙之间转换示意图
赵维炳[12]等通过理论推导得到了考虑砂井地基水平变形和涂抹效应的砂井地基和砂墙地基等效变换公式,即轴对称情况和平面应变情况之间的等效公式。
khp=Dhkhw
(2)
kvp=Dvkvw
(3)
其中,khw、kvw分别是砂井地基水平向和竖向渗透系数;ks为砂井涂抹区渗透系数,β=khw/ks;n=re/rw为砂井井径比,re为砂井影响区半径,rw为砂井半径;s=rs/rw为砂井涂抹区半径与砂井半径之比;B为砂墙间距的一半,bw为砂墙宽度的一半,bs为砂墙地基涂抹区宽度的一半,np=B/bw,sp=bs/bw;L为砂井间距放大倍数,L=B/re;Dh、Dv分别为水平和竖向渗透系数调整系数;khp、kvp分别为调整后的砂墙地基中水平向和竖向渗透系数。
为了在砂墙模型中不用考虑涂抹区尺寸,思路同1.2节中砂井模型,令s=rs/rw=1,kkw/ks=1,np=n=15,sp=bs/bw=1,khp/ksp=1,砂墙厚度的一半取为bw=rw,砂墙间距的一半为B=re,即L=1,其他参数同1.2节,此时可求得水平向渗透系数调整系数Dh=0.2651,khw=ks=kh′,即可求得khp,仍通过一算例来检验上述变换的可行性。
对于砂井地基轴对称情形与平面应变情形之间的等效变换,关键在于保证两种情形下平均固结度和同一深度处平均孔压在任意时刻都要相等或接近[12]。因此选取等效变换前后的地表竖向位移、平均固结度和地表下10 m深度处孔隙水压力进行对比分析,分别如图4~6 所示。由图4和图5可知等效后的砂墙模型在固结时间相等时,前期竖向位移和平均固结度都大于砂井模型,但差值不大,且逐渐减小,固结时间为50 d时,竖向位移误差小于5%;孔隙水压力变化如图6所示,等效前后相比,误差不大,满足工程精度要求,因此该等效变换方法合理。

图4 砂井模型等效对地表竖向位移的影响
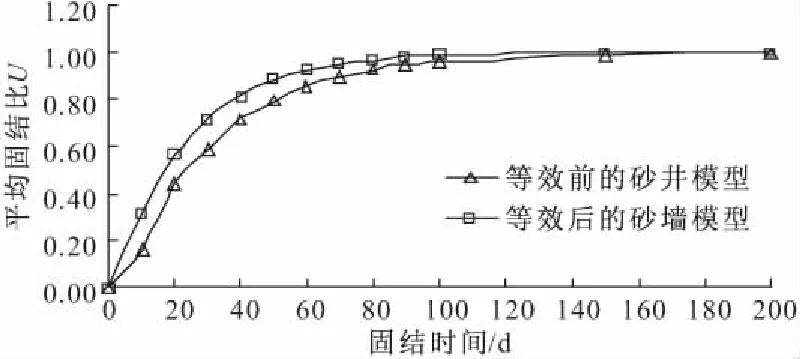
图5 砂井模型等效对平均固结度的影响
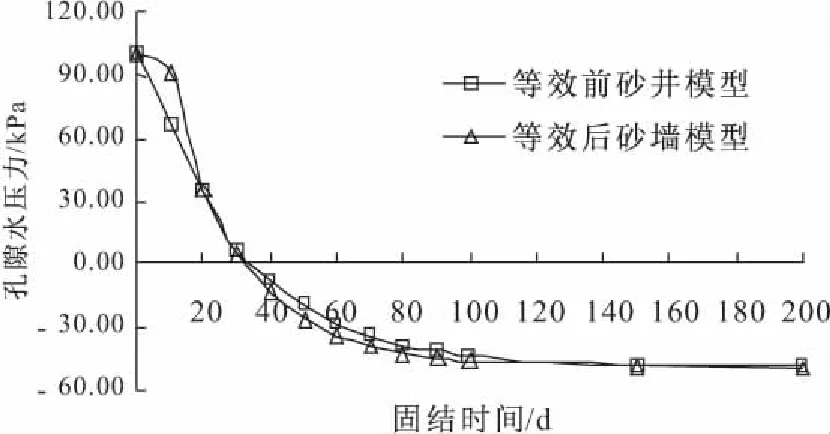
图6 砂井模型等效对10 m深度处孔隙水压力的影响
3 工程实例计算
3.1 计算模型
某吹填土地基采用真空预压法处理,排水袋装砂井直径14 cm,间距2.0 m,处理深度20 m,等边三角形布置。由于加固面积很大,砂井密布,很难全部在计算模型中反映出来,但边界条件对加固区变形的影响必须予以考虑。朱继伟[4]等通过平面有限元计算发现当计算区域的长、宽均大于10 m时,加固区面积对变形影响不大。根据对称性,取模型的一半进行分析,考虑边界对加固区的影响,X方向加固区宽度取为10.5 m,影响区宽度取为3倍加固区宽度,加固区Y方向假设为无限长,即不考虑边界影响,计算宽度取单排砂井影响宽度1.73 m,计算深度取20 m。采用2.3节中方法将砂井等效为砂墙,砂墙间距取为2.1 m(B=1.05 m),其余参数同2.3节,计算模型几何尺寸剖面图和平面图分别如图7(a)、7(b)所示。

图7 计算模型几何尺寸
3.2 计算结果分析
地表最大竖向位移曲线如图8所示,当加固区宽度为10.5 m时,地表最大竖向位移始终比不考虑边界影响时小,固结100 d时为48.77 cm,远小于不考虑边界影响的74.39 cm,说明加固区边界对加固区竖向位移的影响很大。
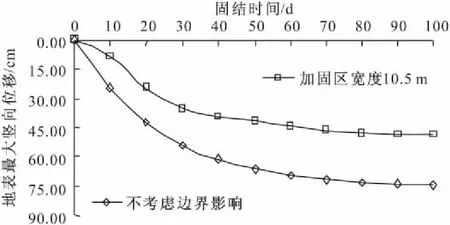
图8 地表最大竖向位移对比
与堆载预压时地基土体发生侧向挤出变形不同,采用真空预压法时地基土体在侧向为收缩变形,如图9所示,为地表水平位移在不同固结阶段随距加固中心水平距离的变化曲线。由图可知地表水平位移总体呈“V” 形分布,地表最大水平位移发生在加固区边界附近,随固结时间的增加而增大,固结100 d时,最大值为22.24 cm,右侧边界附近位移值在1.0 cm左右。
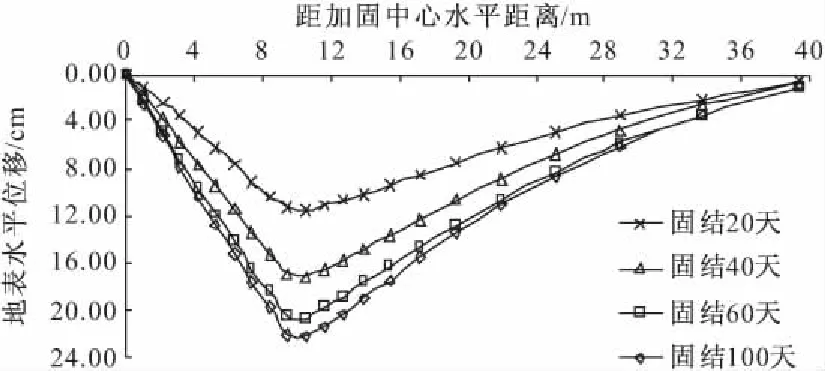
图9 地表水平位移随距加固中心距离变化曲线
地表沉降在不同固结阶段随距加固中心距离的变化曲线如图10所示,地表沉降随距加固中心距离的增大而减小,加固区内地表沉降大于加固区外,最大沉降发生在加固区中心处,总体分布曲线呈“锅底”型,固结完成100 d时,最大沉降为48.77 cm。
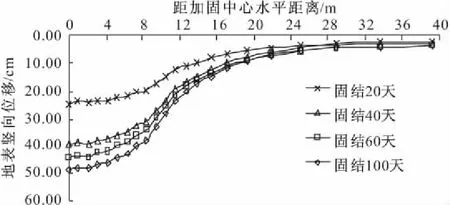
图10 地表沉降随距加固中心距离变化曲线
对加固区边界不同深度处土体侧向位移进行分析,如图11所示,侧向变形曲线总体呈“S”形分布,地表处最大,基底处最小,随固结时间的增大而增大。基底处侧向位移取小值与模型边界条件有关,受底部固定边界的影响较大(模型底部在X、Y、Z三个方向均固定)。
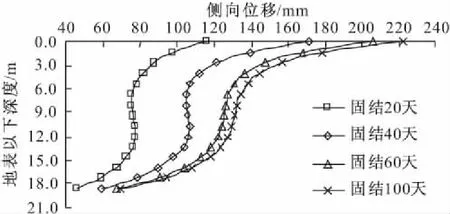
图11 加固区边界侧向位移随深度变化曲线
3.3 加固区面积的影响
真空预压效果和预压区面积大小及长宽比等有关,表1为天津新港现场预压试验实测结果[6]。

表1 预压区面积大小的影响
为研究加固区面积对吹填土地基处理效果的影响,在3.1节计算模型(加固区宽10.5 m)的基础上,分别取不考虑边界影响、加固区宽16.8 m和加固宽度为23.1 m三种情形进行计算,加固区宽度对地表最大竖向位移的影响如图12所示。
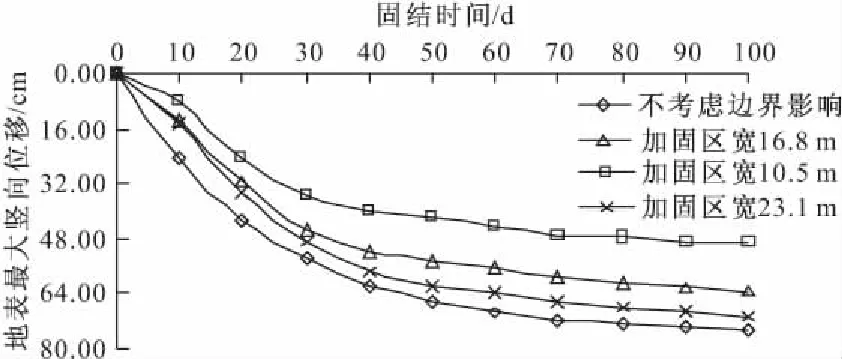
图12 加固区宽度对地表最大竖向位移的影响
由图12可知固结时间相同时,地表最大竖向位移随加固区宽度的增大而增大,固结100 d时,分别为48.77 cm、63.16 cm和70.22 cm,不考虑边界影响时为74.39 cm,由此可见,在数值计算中,加固区宽度的取值对竖向位移计算结果影响较大。根据规范要求,一般采用80%的固结度作为设计要求达到的固结度,取不考虑边界条件影响时固结200 d的地表竖向位移作为最终位移值,达到80%固结度时位移值约为60 cm,根据上述计算结果,加固区宽度(根据对称性取一半宽度)取值应该在16.0 m以上,此时边界对加固区中心点竖向位移的影响可以忽略。
4 结 论
本文对吹填土地基真空预压简化建模方法进行了探讨,利用有限差分软件建模对简化方法进行了验证,采用简化方法对吹填土地基真空预压处理效果进行了分析,得到以下结论:
(1) 将涂抹效应对涂抹区渗透系数的弱化作用均化到单井影响范围土体内是可行的,可以大大减小砂井地基建模的前处理工作量。
(2) 借鉴砂井地基涂抹效应的均化方法,可以建立不考虑涂抹区尺寸的砂墙模型,进一步简化砂井地基三维分析建模难度。
(3) 加固区边界对地表竖向位移计算结果影响较大,为减小边界影响,加固区宽度(根据对称性取的一半宽度)应该在16.0 m以上,此时边界对加固区中心竖向位移的影响可以忽略。
[1] 王 芳, 郭进京, 郑忠成. 吹填土地基处理方法的讨论[J]. 岩土工程界, 2008, 12(6): 15-17.
[2] Shang J Q, Tang M, Miao Z. Vacuum preloading consolidation of reclaimed land: a case study[J]. Canadian Geotechnical Journal, 1998, 35: 740-749.
[3] 陈平山, 房营光, 莫海鸥, 等. 真空预压法加固软基三维有限元计算[J]. 岩土工程学报, 2009, 31(4): 564-570.
[4] 孙立强, 闫澍旺, 李 伟. 真空-堆载预压加固吹填土地基有限元分析法的研究[J]. 岩土工程学报, 2010, 32(4): 592-599.
[5] 朱继伟, 闫澍旺, 孙万禾. 真空预压侧向变形影响因素的研究[J]. 水运工程, 2004, (1): 16-20.
[6] JGJ 79-2002,建筑地基处理技术规范[S].
[7] Yildiz A. Numerical analyses of embankments on PVD improved soft clays[J]. Advances in Engineering Software, 2009, 40: 1047-1055.
[8] Indraratna B, Redana I W. Numerical modeling of vertical drains with smear and well resistance installed in the soft clay[J]. Canadian Geotechnical Journal, 2000, 37: 132-145.
[9] 彭 劼, 刘汉龙, 陈永辉, 等. 真空-堆载联合预压法软基加固对周围环境的影响[J]. 岩土工程学报, 2002, 24(5): 656-659.
[10] 赵常洲. 高速公路软基真空-堆载联合预压加固机理及其数值模拟[D]. 北京:中国地质大学(北京), 2008.
[11] 龚晓南. 高等土力学[M]. 杭州: 浙江大学出版社, 2004.
[12] 赵维炳, 陈永辉, 龚友平. 平面应变有限元分析中砂井的处理方法[J]. 水利学报, 1998, (6): 53-57.

