滨海吹填土固结蠕变特性试验研究

雷华阳，刘景锦，郑 刚，贾亚芳，康景文，孙 铁

(1.天津大学 a.土木工程系， b.滨海土木工程结构与安全教育部重点实验室， 天津 300072；2.中国建筑西南勘察设计研究院有限公司， 四川 成都 610081；3.建设综合勘察研究设计院有限公司， 北京 100007)

近年来，由于东南沿海地区国土资源面积的减少，使得围海造陆工程迅速发展，大面积的新近吹填土地投入建设和使用，使得大量工程建设在新近吹填成陆的地基之上。然而诸多的工程实践表明，即使是经过加固的吹填土在经历自然沉积排水后含水量极高、强度极低，基本不具承载能力[1]。天津滨海地区工程实践表明，在建筑物或构筑物荷载的长期作用下，即使在主固结基本完成后，地基土仍然会发生显著的蠕变变形。如天津经济开发区近十年来已发生了近10 cm的附加沉降，基本上都是由蠕变变形造成的。建于回填软土地基上的上海浦东开发区，观测到的附加变形超过了天津开发区的蠕变速率。由此可见，软土地基存在的变形问题严重影响着天津滨海新区和其它软黏土地区的发展建设，有必要进行深入细致的研究，即探讨滨海软土的变形特性以及不同成因土体差异性对其变形特性的影响将为解决围海造陆实际工程中的关键科学和技术问题提供依据，同时也为保证围海造陆形成陆域的长期稳定和可持续发展提供理论依据和技术支持。

国内外学者针对软土的固结蠕变特性进行了大量的试验和理论研究。如Bjerrum L[2]早在1967年进行蠕变研究时，就提出固结和蠕变同时发生；Davison L R等[3]对Bothkennar土进行了一系列一维固结试验研究，得出不同深度、应变速率对屈服应力的影响规律；沈杰、余群等[4]采用分别加载方式，研究了湿软土壤的蠕变特性，得出应变速率对数和应力以及时间对数呈现线性的结论。王常明、肖树芳等[5]采用一维分级加载对上海、珠海、深圳等典型地区的海积软土进行蠕变试验研究，得出海积软土的一维固结蠕变的应力-应变关系是非线性、不可逆、与时间有关的。刘汉龙等[6]采用改进的、可施加负压的三轴仪开展了真空预压、堆载预压以及真空-堆载联合预压作用下软土的固结蠕变试验；朱鸿鹄等[7]针对珠江三角洲软土进行了排水和不排水条件下软土的蠕变特性研究；周秋娟，陈晓平[8]对广州南沙原状软土进行了室内三轴压缩试验、三轴蠕变试验和一维固结试验，系统地探讨了软土的蠕变变形特性；刘克瑾，闫澍旺[9]等通过改装的三轴仪对滨海新区软黏土的蠕变特性进行了试验分析，重点探讨了施工期的土体流变性质，建立了相应的计算模型；国外许多学者也对软黏土的蠕变特性进行了研究和探讨[10～12]，建立了软黏土的蠕变模型[13,14]，探索了软土的次固结系数和蠕变变形的计算方法[15～17]。

由此可见，关于软黏土蠕变特性方面的研究成果较为丰富，但以往研究的是针对天然沉积软土，对于新近吹填的软土研究较少。而新建吹填成陆的软黏土与自然沉积的土体从成因、结构、矿物组成及空间分布上都有较大差异。

基于上述分析，本文利用改装的单向固结仪，开展不同加荷方式及不同高度下滨海吹填土的蠕变特性试验研究，获得应变、应力和时间关系，并与正常沉积软土的试验结果进行对比分析，着重探讨不同压力条件下土体的次固结系数变化特点。

1 试验设备及具体方法

1.1 试验土样及设备

试验土样分别取自天津滨海新区典型淤泥质黏土和中心渔港围海造陆真空预压处理后吹填土，取土深度为2.0～5.0 m，基本物理力学特性指标如表1所示。

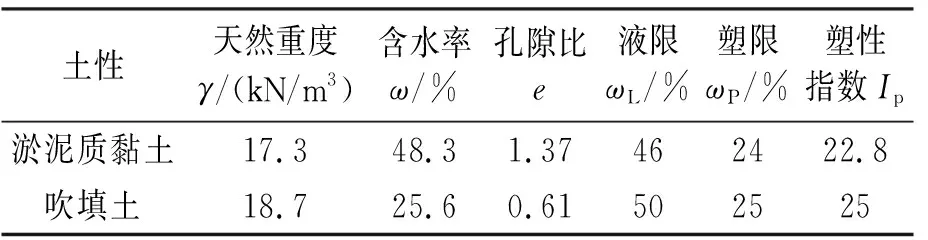
表1 土样的物理力学参数指标统计表

一维固结试验采用三联高压单杠杆固结仪，为适应试验条件要求，将固结仪进行改装，如图1所示。

图1 WG型单杠杆固结仪

1.2 试验方案

一维固结试验均选用面积为30 cm2，高度分别为2 cm和6 cm的两种类型。加载方式均为分级加载，每级荷载以定时观测变形小于0.005 mm/d为稳定标准，待一级荷载下变形稳定后加下一级荷载，数据采集记录采用TWJ微机数据采集处理系统。具体试验加荷方案如表2所示。

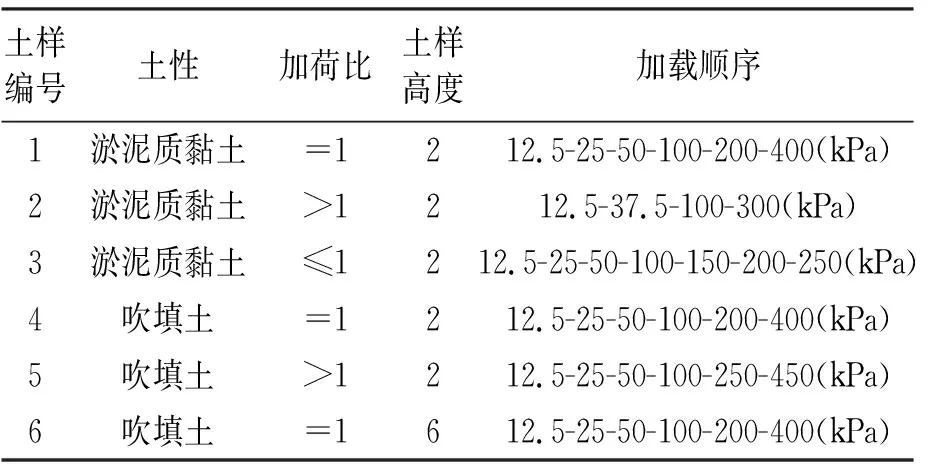
表2 固结蠕变试验方案表

2 试验结果整理与分析

2.1 分级加载条件下变形特性对比

图2为相同条件下天津滨海典型淤泥质黏土和围海造陆真空预压处理后吹填土分级加载时应变-时间对比曲线，从图中可以看出：不同土体相同荷载条件应变发展趋势一致，即加载瞬间发生瞬时弹性响应，随后产生随时间而增长的变形。当应力水平较低时，变形的速率随时间的增长而逐渐变缓，当达到一定时间后，变形不再增长，最终变形趋于一个稳定值，此时两种土体应变量差别不明显；随着荷载的逐渐增加，当荷载达到50 kPa时，滨海淤泥质软黏土加载瞬时变形较大，最大可达到5.77%，而经真空预压处理后吹填土随着荷载水平的提高，在50 kPa加荷瞬间变形量值基本在0.07%范围内，此时两种土性的变形量值开始出现明显的差异。这主要是因为，未经加固的天津滨海软土初始孔隙比较大，而经真空预压加固后的吹填土，相同荷载作用下孔隙比较小，土体更密实，变形较小。

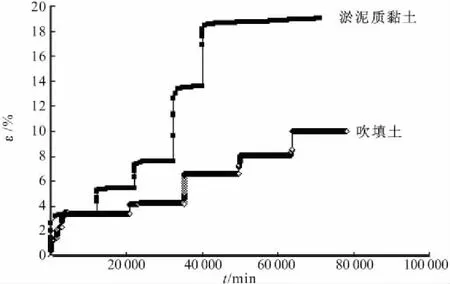
图2 分级加载条件下土体应变-时间曲线

图3 淤泥质黏土分级加载下土体双对数坐标下的变形与时间的关系曲线

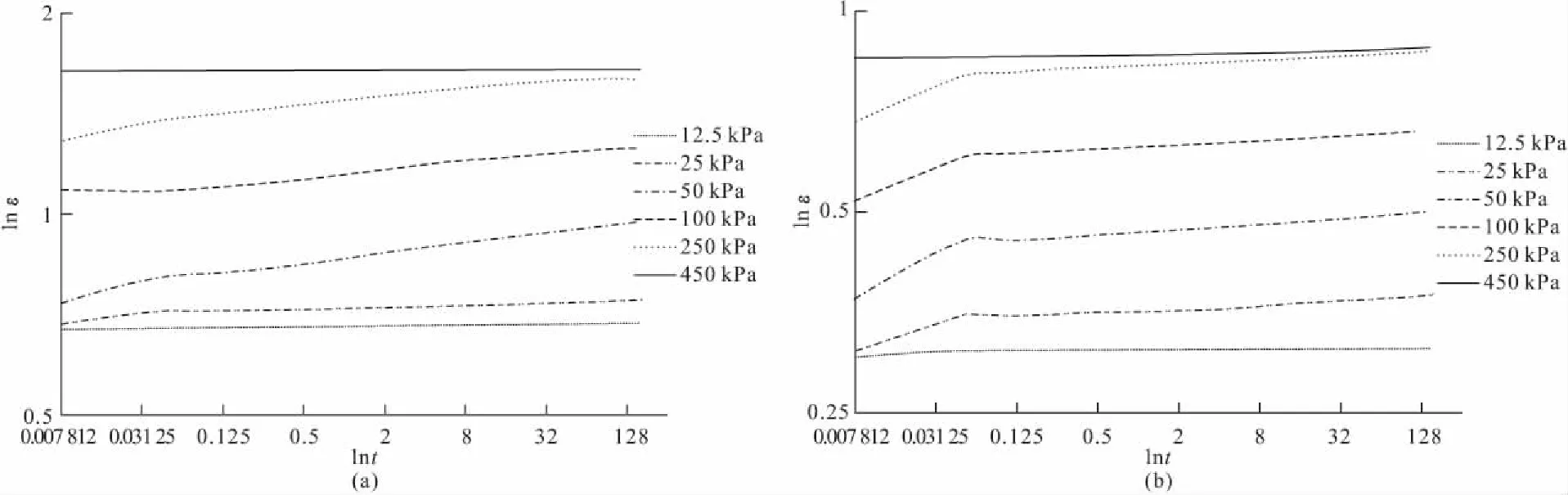
图4 吹填土分级加载下土体双对数坐标下的变形与时间的关系曲线

图3和图4分别为滨海淤泥质黏土和真空预压加固后吹填土分级加载时双对数坐标下变形随时间变化的曲线。可以看出，当应力水平较低时，两种土体试验曲线呈现出折线线性关系；当应力水平较高时，曲线逐渐呈现线性发展，各级荷载下的双对数曲线表现为一组平行直线。说明存在一个临界荷载值，且认为该荷载大小对软土的次固结存在一定影响。

2.2 吹填土变形特性的影响因素分析

2.2.1不同加荷比条件下的变形特性

图5为不同加荷比条件下分级加载吹填土的应变时间关系曲线。曲线整体趋势与相同条件下滨海软土的发展趋势一致，加载瞬间发生瞬时弹性响应，随后产生随时间而增长的蠕变变形。

加荷比>1时吹填土最终蠕变量达到4.7%，比相同深度下加荷比=1的吹填土体最终蠕变量高出1.2%。可以看出，加荷比对于吹填土体蠕变增长有较大影响。这与相同条件下不同加荷比时滨海软土得出结论一致，即加荷比越大，土体最终蠕变变形越大。

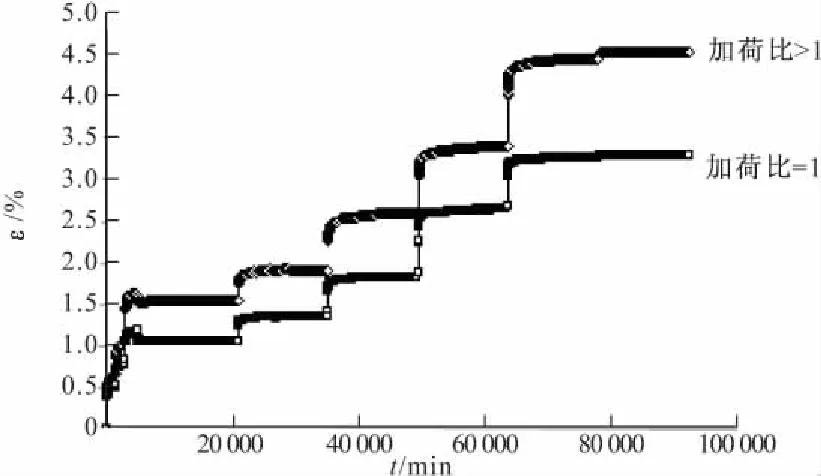
图5 分级加载条件下土体应变-时间曲线

2.2.2不同高度下吹填土的变形特性分析

以往学者的试验，多是针对高度2 cm的土样进行研究，而对于试验中不同高度的土样研究较少。由于土体的各向异性较强，且为了更好地反映土体的实际情况，所以有必要进行不同高度试样的固结试验。因此，在进行吹填土固结试验中，将2 cm试验环刀加高到6 cm，对一组6 cm试样进行了试验研究。

图6为不同高度吹填土试样分级加载条件下应变-时间关系曲线，可以看出：不同高度试样的应变时间曲线随时间发展趋势一致，均是在各级荷载作用下，先有一个瞬时弹性响应，然后随时间发展蠕变趋于稳定；不同高度试样最终蠕变量差别较大，表现为2 cm试样最终蠕变量为3.5%，而6 cm试样最终蠕变量达到7.4%，6 cm高度试样最终蠕变量达到2 cm试样的2.1倍。可见，对于不同高度试样的试验研究非常必要。

图6 分级加载条件下土体应变-时间曲线

2.3 次固结系数变化规律分析

在分析软土累积应变的长期沉降变化规律时，次固结引起的地面沉降不容忽视。目前很多土工试验规范都没规定次固结系数这个指标，但是在港口、码头工程中遇到厚层软土时需要该指标，这是个很大的缺陷。为此，试验针对天津滨海围海造陆形成的吹填地基土，进行了次固结系数的测定，得到图7、8，为建立吹填土蠕变-固结耦合分析提供了依据。

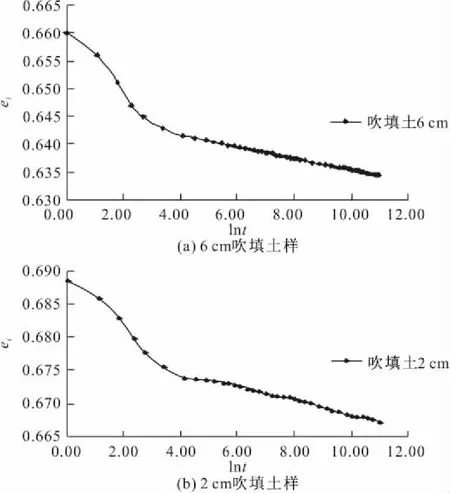
图7 不同高度下吹填土样的固结曲线

次固结系数计算方法采用下式[13]求出：

Ca=-Δe/(lgt2-lgt1)

(1)

其中，t2为次固结量的计算时间，单位为s；t1为固结度为100%的时间，单位为s。

本文依据此方法，得到2 cm和6 cm吹填土样固结e-ln(t)曲线(图7)，为了便于研究，笔者选取了固结曲线后接近直线段一部分曲线作图分析，通过拟合计算得到两种高度下土样次固结系数分别为0.0012和0.0016，试验表明高度相差不大的试验土样次固结系数相差不大。

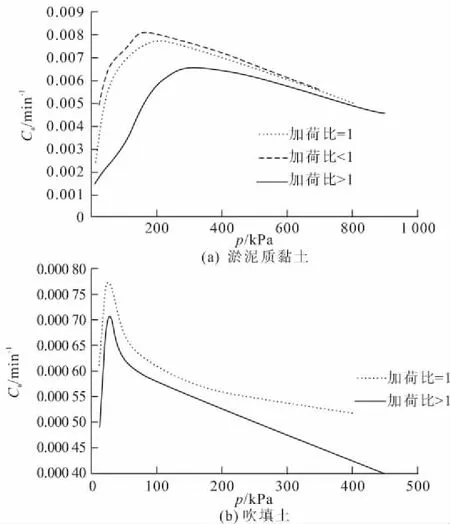
图8 分级加载条件下次固结系数随压力的变化曲线

图8为不同条件下次固结系数与压力的变化关系曲线，从中可以看出：

(1)次固结系数跟荷载大小有关。次固结系数先随着压力的增大而增大，达到峰值之后会降低，一般最大值出现在先期固结压力之后。究其原因，是因为对于结构性软土而言，胶结结构能够约束土骨架的蠕变变形，胶结性越强，对次固结系数的阻碍越强，次固结系数就越大。当压力逐渐增大时，胶结性增强，次固结系数增大，但是当压力超过土体的结构屈服压力时，土体的胶结性逐渐被破坏，对次固结的阻碍作用减弱，则次固结系数逐渐减小。

(2)从图8(a)可以得到，次固结系数跟加荷比有关。加荷比<1时，次固结系数峰值较高，峰值处对应荷载较低；加荷比=1时，与前者基本相似；加荷比>1时，峰值较低，峰值处对应荷载较高。究其原因，可能是由于当加到相同荷载时，在加荷比较小的情况下，每一步的荷载增量较小，对土体逐渐压密，对次固结的阻碍作用就越大，所以在加荷比小的时候就产生较大的次固结系数。

(3)各级荷载作用下，加固后吹填土次固结系数比未经加固正常沉积的淤泥质黏土小，次固结系数出现转折点的荷载值较小。

3 结 论

(1)通过对天津滨海新区典型淤泥质土和围海造陆处理工后吹填地基土进行一维固结对比试验，认为两种软土均具有明显的非线性蠕变特性，相同试验条件下，两种土体试验变形增长不一致，表现为在较低荷载水平下，两种土体变形差别不大，随着荷载等级加大，变形差别逐渐加大，吹填土的次固结变形与天然沉积软土相比较大。

(2)次固结系数与加荷比和荷载等级有关，表现为次固结系数随荷载增大先增大后减小，峰值随加荷比增大而减小；试样高度对于土体次固结系数有一定影响，但不十分明显。

(3)吹填土一维固结蠕变特性受加荷比、试样高度等因素影响：不同加荷比对于吹填土体蠕变量增长影响不同，表现为加荷比<1、=1、>1试验条件下，土体最终蠕变量依次增大；不同高度吹填土试样的应变时间曲线随时间发展趋势一致，但最终变形量差别较大，表现为6 cm试样最终变形较大，但最终应变差别不大。

[1] 侯 钊，陈 环，钱 征，等.天津软土地基[M].天津：天津科学技术出版社,1987.

[2] Bjerrum L. Engineering geology of Norwegian normally-consolidated marine clays as related to settlements of buildings[J]. Geotechnique, 1967,17(2):83-118.

[3] Nash D F T，Sills G C，Davison L R. One-dimensional consolidation testing for soft clay from Bothkennar[J].Geotechnique，1992,42(2):241-256.

[4] 沈 杰, 余 群. 湿软土壤蠕变特性的试验研究[J]. 北京农业工程学报,1989,9(3):20-24.

[5] 王常明,肖树芳,夏玉斌，等. 海积软土的固结蠕变性状[J]. 长春科技大学学报,2000,30(1):57-60.

[6] 刘汉龙，扈胜霞，Ali Hassan.真空-堆载预压作用下软土蠕变特性试验研究[J].岩土力学，2008，29(1)：6-12.

[7] 朱鸿鹄，陈晓平，程小俊,等.考虑排水条件的软土蠕变特性及模型研究[J].岩土力学，2006，27(5)：694-698. .

[8] 周秋娟，陈晓平.软土蠕变特性试验研究[J].岩土工程学报，2006，28(5)：626-630.

[9] 刘克瑾，闫澍旺.天津滨海新区软黏土的流变特性研究及无屈服面黏塑性模型[J].岩土力学，2010，31(5)：1431-1444.

[10] Yin J H,Graham J. Elastic visco-plastic modeling of one-dimensional consolidation[J]. Geotechnique, 1996, 46 (3) :515-527.

[11] Lin H D, Wang C C. Stress-strain-time function of clay[J].Journal of Geotechnical and Geoenviromental Engineering, 1998,124 (4) :289-296.

[12] Puswewala U G A, Madurapperuma M A K M. Numerical implementation of a constitutive model for soil creep[J]. Journal of Mechanics of Materials and Structuners,2008, 3(10):1857-1874.

[13] 孙德安，申海娥.上海软土的流变特性试验研究[J].水文地质工程地质，2010，37(3)：74-78.

[14] 于新豹，刘松玉，缪林昌.连云港软土蠕变特性及其工程应用[J].岩土力学，2003，24(6)：1001-1006.

[15] 雷华阳，肖树芳. 天津软土的次固结变形特性研究[J].工程地质学报，2002，10(4)：385-389.

[16] 田淑娟，王新中，张米军.测定土的次固结系数及方法[J].水科学与工程技术，2010，(3)：52-53.

[17] 陈晓平，朱鸿鹄，张芳枝，等.软土变形时效的试验研究[J].岩石力学与工程学报，2005，24(12)：2142-2148.