高速永磁电机定子温度场的计算与分析

孔晓光，王凤翔，林爱军

（1. 沈阳化工大学信息工程学院，沈阳 110142；2. 沈阳工业大学电气工程学院，沈阳110870）

前言

高速电机由于体积小、功率密度大和效率高，正在成为电机领域的研究热点之一。[1]其缺点是单位体积损耗大，以及因散热面积小造成的散热困难。当冷却空气不能有效的带走电机内部产生的热量时，就会造成电机温升过高或温升不均匀。因而准确的温升计算和合理的通风设计对高速电机的安全运行至关重要。

本文以一台额定转速为60000r/min的2极24槽高速永磁电机为例，高速电机的定子采用了一种有利于提高转子刚度和冷却效率的环形绕组。环形绕组下层边分布在定子铁心的24个槽中，而上层边分布在定子轭部的24个槽中。这样的结构可以增加定子表面的通风散热面积，使得冷却气流不但能够有效的冷却定子铁心，也能直接冷却定子绕组，提高了冷却效率。为了能够准确的描述电机定子温度场的分布情况，本文将基于三维流体场分析得到的定子温度分布与传统的等效热路法计算的温度场结果和电机温升试验值进行比较，从而验证了电机内流体场和温度场之间存在着耦合关系。

1 定子轴向通风系统流体场模型和温度场的计算

1.1 定子通风系统结构

该 75kW 高速永磁电机采用强迫风冷方式，电机中的热量主要是通过电机定子表面与空气流的热交换被带走。进入高速电机的定子侧气流分三个方向通过，即外风道、内风道和气隙，如图1所示。从整个电机的结构看，外风道对气流的空气阻力最小，所以风量最大；其次是内风道，由于高速电机转子表面转速很快，所以经过气隙流出的空气很少，几乎可以忽略不计。

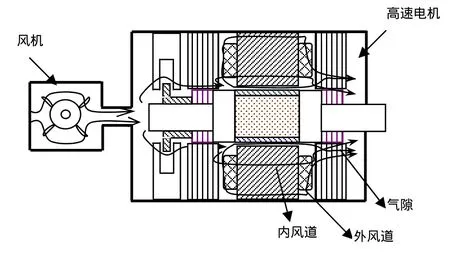
图1 高速电机通风系统示意图

1.2 流体场通用控制方程

流体的流动状态根据其流速的大小、流体的性质以及流通路径可以分为层流和紊流两种。雷诺数的大小决定了粘性流体的流动特性。当电机中冷却空气流速很小时，此时空气流态可以认为是层流的；而高速电机的转子表面速度很高，气隙中流体的雷诺数很大，属于紊流状态。根据粘性流体力学理论[2]，在紊流的流场条件下，遵循物理守恒三大定律可以得到如下的通用控制方程的矢量形式[3-4]。

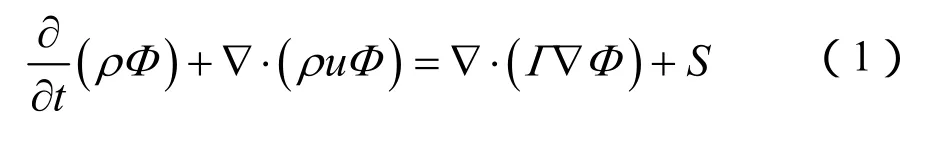
写成一般形式为

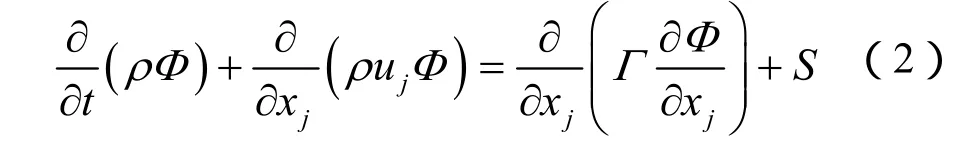
对式（2）采用有限体积法进行积分，得到如下形式

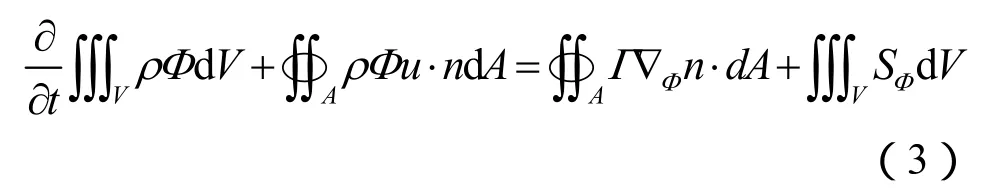
其中：Φ为通用变量；Г为广义扩散系数；S和SΦ是与Φ对应的广义源项；ρ为流体密度[5-7]。

1.3 求解域物理模型及假设与边界条件

由于发电机定子区域的流动与换热问题在圆周方向具有对称性，可以选择整个电机的1/24作为分析对象，建立三维实体模型并在gambit 中进行网格剖分。

应用Fluent进行求解时，由于电机运转时内部空气的的流动处于高Re数区，因此在流动模型的选取时采用了RNGk-ε模型，同时有热量交换。在定子铁心和线圈上需附加能量源项，其中定子线圈上的能量密度为 61920W/m3，定子铁心上的能量密度为172872W/m3。

考虑电机风路的对称性，假设冷却空气经过离心风机加压后进入到各个风道的风量相同且空气垂直风道入口进入内通风道。在通风道入口施加速度入口边界条件，以 Velocity—inlet 边界设定外风道的气体流入速度为19m/s，内风道的气体流入速度为14m/s。进入的空气温度为 293K（20℃）。出风侧端面设为Pressure—outlet 边界，边界压力设为0Pa 。固体和流体交接面设为耦合边界，其余区域采用默认边界。其模型及边界条件的划分如图2所示，其中A为周期性边界面，B和C为内外通风道入口，D和E为压力出口，F为转子和气隙交接面，在此面上设定转子与空气相对运动速度及粗糙度等因素。

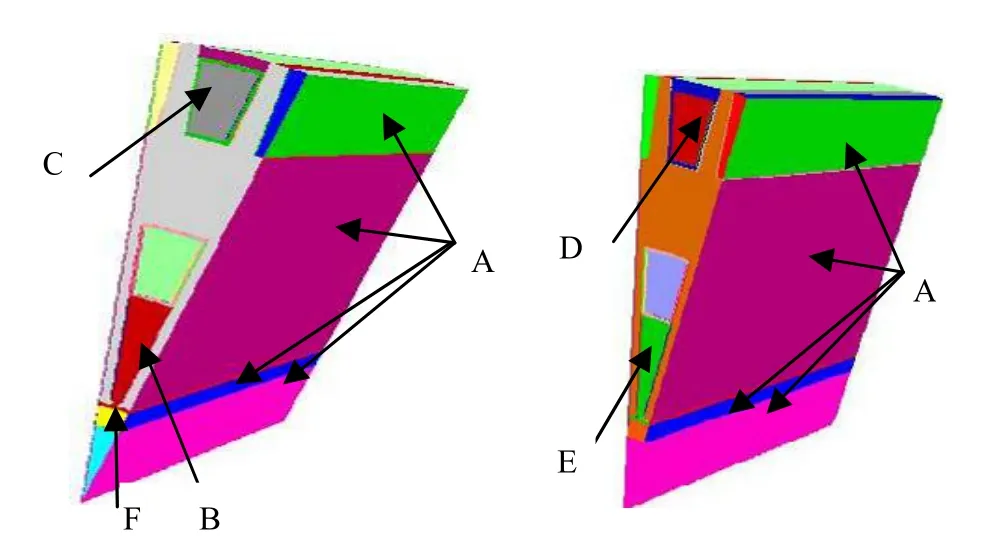
图2 高速永磁电机流体场分布模型

1.4 流体场与温度场的数值计算与分析

在直角坐标系中建立永磁电机的通用稳态热传导方程，并在给定边界条件及三维流体场计算的基础上，通过迭代计算得到永磁电机空载运行在60000r/min时定子温度场分布和定子轴向通风系统的流速分布，分别如图3和图4所示。

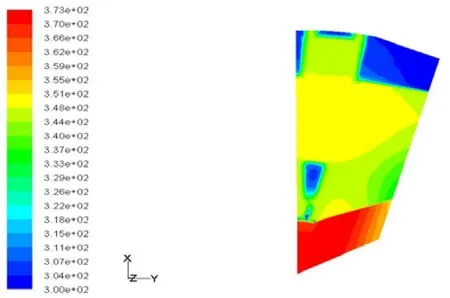
图3 高速永磁电机定子的温度分布

从图3中可以看出高速永磁电机在60000r/min空载运行时，无论内风道还是外风道从出风口吹出的空气的平均温度高于进风口，这说明电机发出的热量已由冷却空气带走。计算区域内定子的温度自进风端沿轴向逐渐递增，在靠近出风口一侧的齿部附近达到最高，温度大约为76.8℃。内绕组的温度要高于外绕组的温度。

图4 定子轴向通风系统的流速分布

2 基于等效热路法的电机定子温升分析

电机温升的计算还有一种常用的方法即等效热路法[8-11]。这种方法是把温度场简化为带有集中参数的热路进行计算，其计算的准确度很大程度上取决于通风和散热的系数。由于热路法在电机的计算上已经十分成熟，所以本文也采用了热路法对电机定子进行了温升分析。

由于研究的高速永磁电机轴向气流较大，电机的定子和转子之间无热交换，因此定子和转子可以组成各自的热路。对于定子而言，定子铁心、定子绕组构成热路的热源。

根据电机设计和传热学相关知识，等效热路法的热阻可分为传导热阻和散热热阻。热量从高速电机的绕组和定子铁心传给冷却空气，其热流路径要经过两个热阻，即传导热阻Rλ和散热热阻Rα。

其中传导热阻如下：

式中：δ为热路传导长度，λ为材料热导率，A为等温面的面积。

热对流传递方式中散热热阻如下：

式中：α为介质的散热系数，A为等温面的面积。

对于高速电机的定子最主要的是计算铁心和的绕组的温升。这些部件既是热源又是导热介质，在电机中它们的温度在空间上总是按一定的规律变化的，这样就有了平均温升和最高温升之分。虽然电机的发热温升以最高温升为准，但在计算时，通常可以只计算发热部件的平均温升。因为最高温升与平均温升之间是有一定的规律和联系的，所以同样可以用平均温升来衡量电机的发热情况。

图5为高速电机定子集中参数等效热路图。其中1代表定子铁心损耗、2代表外绕组铜耗、3代表内绕组铜耗、4代表绕组端部损耗。假定定子外表面和定子内表面冷却介质温度为θa，气隙表面气流温度为θg，而绕组上部、绕组下部、绕组端部和铁心的温度分别为θw1、θw2、θwe和θFe。

利用节点电压法，可写出定子热平衡方程，以矩阵形式表示如下

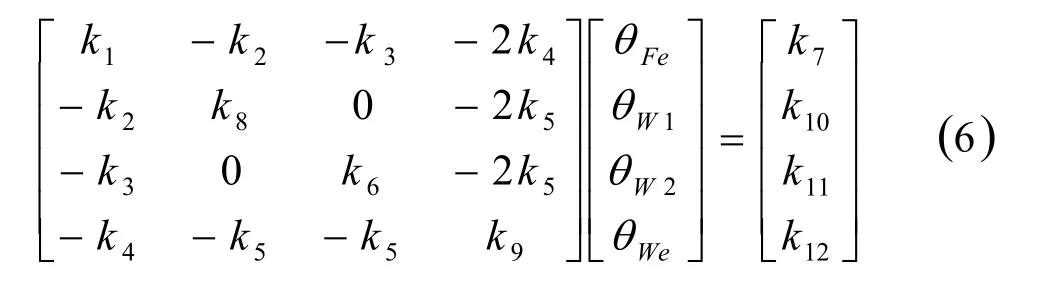
其中k1～k12分别是热路法的等效参数。

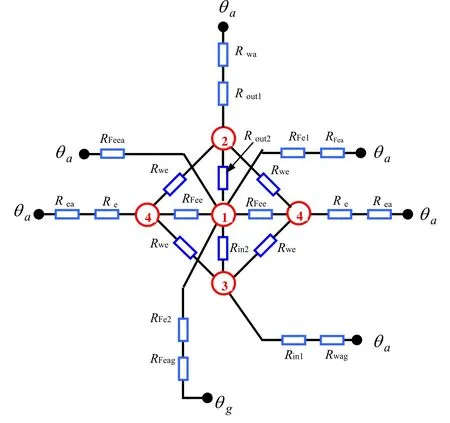
图5 定子集中参数等效热路图

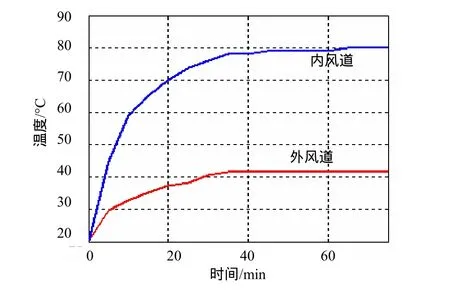
图6 24槽高速永磁电机内外通风道温度变化

通过有限元法计算求得高速电机定子空载运行时铁耗和铜耗。24槽高速永磁电机在60000r/min运行时，内外通风道温度变化曲线如图6所示。通过图6可知θg=80℃，θa=41.6℃，将通风道温度及等效热路图中的计算热阻代入式（6），通过MATLAB软件可以求得电机定子不同部位温度分别为：铁心温度为67.8℃ ，外绕组温度为64.9℃ ，内绕组温度为66.8℃，绕组端部温度为65.6℃。

3 高速永磁电机定子温升试验

高速永磁电机试验样机和定子温度检测装置如图7和图8所示，样机采用6个热敏电阻测量定子绕组和定子铁心的温升，其位置分别放在内槽和外槽内，将热敏电阻引线引出接上专用测温表即可测出温度。对于电机进风口和出风口风温的测量可以采用热电偶。

图7 高速永磁电机试验样机

图8 定子温度检测装置

表1 60000r/min时电机定子温度的对比

通过监测电机的两个出风口和轴身端部的温度，发现空载运行约75min后电机达到稳定温升。此时电机外风道出风口处稳定温升的温度为42.1℃，电机内风道出风口达到稳定温升时的温度为80℃。实测电机定子的温度为78℃，这与基于流体场和温度场耦合分析计算的电机空载运行时的定子温升分析结果基本吻合。而等效热路法虽然计算比较简单但是精度不高，与实际值之间存在着一定的误差。表1是基于不同计算方法的75kW的高速永磁电机定子温升与实测值的对比。

4 结论

要想准确地计算定子温度场，对电机轴向通风沟的流体场分析是必要的；而且从两种解析方法的对比来看，采用基于流体场计算的温度场的计算结果与实际值更加接近。这表明所采用的基本假设和边界条件比较合理，也说明了温度场与流体场之间存在着耦合关系。

从定子温度场的分布来看，由于冷却介质的温度在入口处较低，因此最低温度出现在定子通风道入口上，最高温度出现在靠近出风口一侧的齿部。

[1]Wang Fengxiang, Zong Ming, Zheng Wenpeng, et a1. Design features of high speed PM machines[C].The 6thInternational Conference on Electrical Machines and Systems (ICEMS 2003), Beijing China, 2003.

[2]章梓雄, 董曾南. 粘性流体力学[M]. 北京: 清华大学出版社, 1998.

[3]章本照, 印建安, 张宏基. 流体力学数值方法[M].北京: 机械工业出版社, 2003.

[4]Shanel M, Pickering S J, Lampard D, et al.Application of computational fluid dynamics to the cooling of salient pole electrical machines [J]. ICEM,2000: 338-342.

[5]Yao Ruoping, Rao Fangquan. Research on stator thermal field of evaporation cooling hydro-generator[J]. Proceedings of the CSEE, 2003, 23(6): 87-90 (in Chinese).

[6]Luan Ru, Fu Deping, Tang Longyao. Study on temperture distribution in new evaporative cooling asynchronous generator [J]. Proceedings of the CSEE, 2004, 24(8): 205-209 (in Chinese)．

[7]Rajaopal M S. Seetharamu K N. Finite element analysis of radial cooled rotating electrical machines[J]. International Journal of Numerical Methods for Heat & Fluid Flow, 1999, 9(1):18-38.

[8]程福秀, 林金铭. 现代电机设计[M]. 北京: 机械工业出版社, 1993.

[9]丁瞬年. 大型电机的发热与冷却[M]. 北京: 科学出版社, 1992.

[10]魏水田. 电机内热交换[M]. 北京: 机械工业出版社, 1998.

[11]王述成, 詹琼华, 叶华峰. 采用热路图法计算开关磁阻电机温升[J]. 微电机, 2004, 37(4): 16-18.