船舶垂荡与纵摇耦合运动频率散射机制研究
, ,
(海军工程大学 船舶与动力学院,武汉 430033)
1948年Davidson[1]对顺浪中船舶操纵性问题进行了研究,Rydill[2]仅考虑了Froude-Krylov波浪扰动后得到了波浪中船舶可控和不可控运动的线性分析,Eda[3]在线性操纵性方程中叠加了谐振形式的波浪力,在线性理论下得到了波浪中船舶航向稳定性结果,Eda[4]又在PD操舵规律下研究了波浪中船舶的航向控制稳定性。朱军[6]等人采用切片理论方法计算入射波浪力,代入到波浪操纵性运动方程中模拟计算了操纵运动,陈俊峰[7]又简化了计算模型,采用相同的方法数值模拟了波浪中操纵与横摇运动。文献[8]基于规则波浪中船舶摇荡运动的不规则现象[9-11],提出了遭遇频率散射的概念,开始关注波浪中船舶操纵对摇荡运动的影响,并初步研究了航速和航向引起的散射机制,给出了航速散射在顶(顺)浪效率最高,航向散射在正横浪效率最高的结果。单自由度遭遇频率散射计算阐明了船舶遭遇频率散射的形成的机理,得到摇荡运动方差有显著降低的结论。
本文研究船舶纵向速度振荡对垂荡与纵摇耦合运动的影响机制,建立耦合运动响应模型,计算遭遇频率散射强度和散射系数变化对耦合运动的影响,讨论相关的规律。
1 船体水动力计算
1.1 坐标系及运动关系
为了描述船舶的摇荡运动,建立右手直角坐标系,见图1。
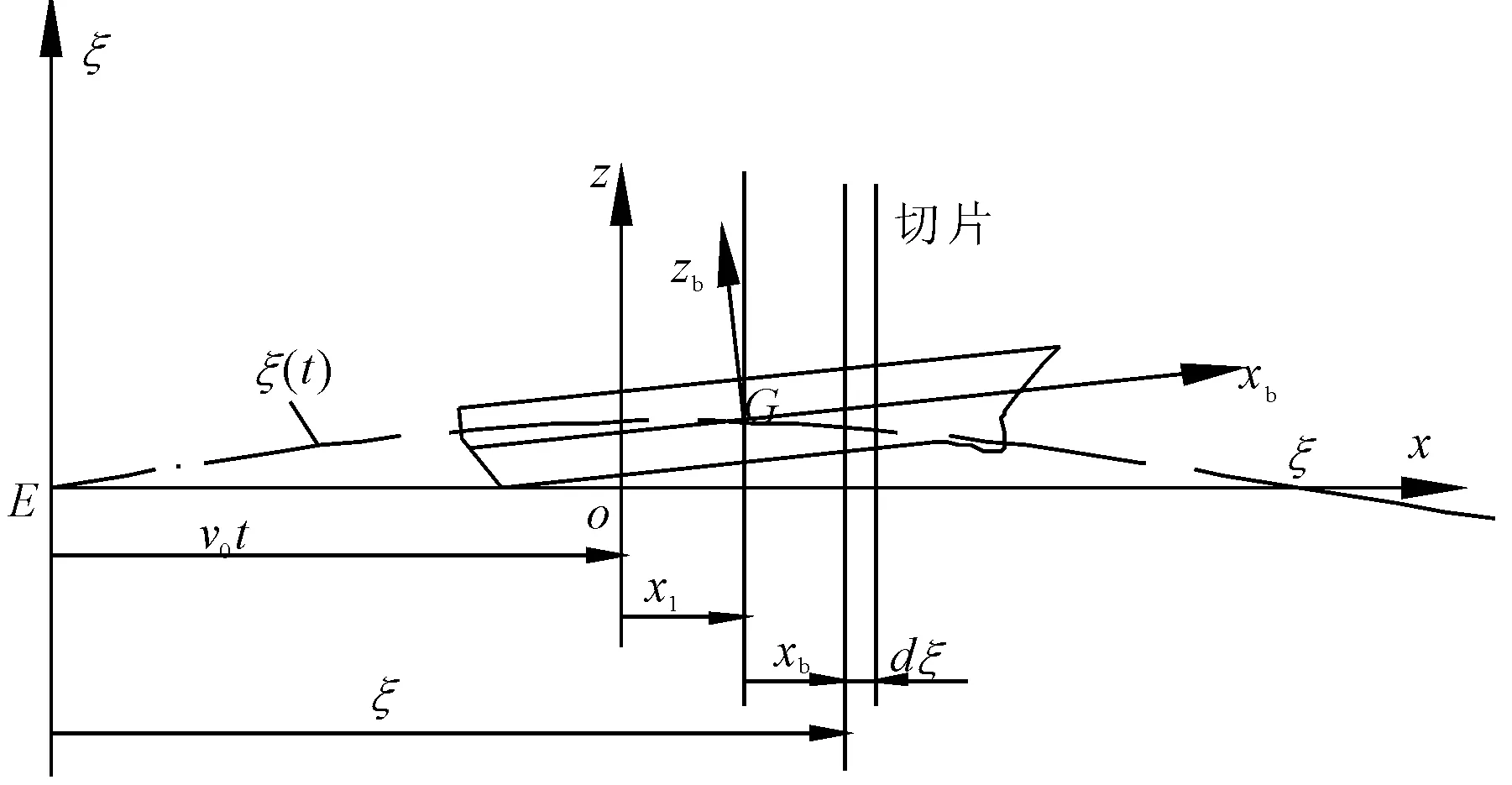
图1 运动坐标系
1)固定坐标系Eξηζ。坐标系固定于地球,ξEη平面与静水面重合,Eξ轴垂直向上为正,用于描述波面升高ζ和船体垂向位移z。
2)平移坐标系oxyz。xoy平面与静水面重合;当t=0时,xoz平面与船舶中纵剖面重合,原点o与E点重合,并在船重心G的垂直线上;随船以等速度v0沿oξ方向运动时,可用于描述船体匀速运动,该坐标原点移动距离为v0t。
3)物体运动坐标系Gxbybzb。原点在船舶重心G上,xbGyb平面平行于静止时设计水线面,Gxb指向船艏,xbGzb平面在船舶中纵剖面上,Gzb轴垂直向上为正,坐标系与船一起平移和振荡。
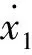
当纵倾角很小时,忽略船体纵倾角引起纵向位移的高阶小量,船体切片纵向坐标(见图1)可表示为
ξ=v0t+x≈v0t+x1+xb
(1)
由坐标系间关系和式(1),可得到如下表达式
(2)
于是船体纵向振荡位移为
(3)
1.2 规则波浪数学表达式
假定波浪为深水规则波,振幅为ζa,波数为k,圆频率为ω,传播方向沿Oξ轴负方向,即船舶处于顶浪状态,在固定坐标系下波面升高的数学表达式为
ζ=ζacos(kξ+ωt)
(4)
波浪相位可表达为
kξ+ωt=k(v0t+x1+xb)+ωt=
(ω+kv0)t+k(x1+xb)=ωe0t+kx
式中:ωe0——船体稳定航速遭遇频率,
ωe0=ω+kv0。
得到
ζ=ζacos(kξ+ωt)=
ζacos[k(x1+xb)+ωe0t]
(5)
式(5)对时间求导数,于是有
(6)
1.3 船体水动力数学表达式
基于弗劳德-克雷洛夫(Froude-Krylov)假定,只考虑静水压力作用,海水密度为ρ,重力加速度为g,切片水动力由船体垂荡位移z、纵摇角ψ和波面升高ζ三项变化引起的浮力、阻尼和惯性力,分别如下。
切片浮力
(7)
切片阻尼力,其中Nz为切片阻尼系数
(8)
切片垂向惯性力,其中mz为切片附加质量,由于
(9)
将切片水动力沿船体纵向积分,得到纵向水动力和力矩如下。
(10)
(11)
2 船舶垂荡与纵摇耦合运动方程
2.1 纵摇与垂荡耦合运动方程建立
根据牛顿第二定律,惯性力和外力平衡,得到
(12)
将式(10)和式(11)代入到式(12)中,得到如下纵摇与垂荡耦合运动方程。
(13)
其中,式(13)左端12项系数如下。
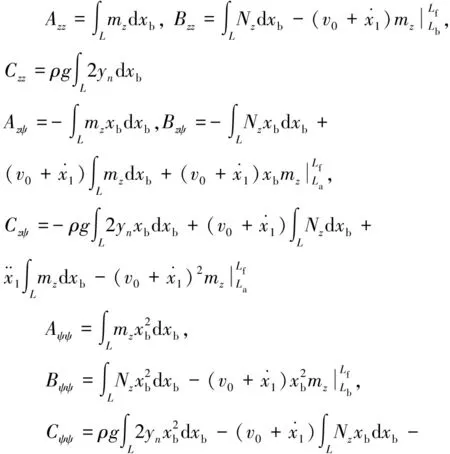
(14)
式(14)中La为船艏坐标,Lf为船艉坐标。
式(13)右端4项系数如下。
(15)
式(15)中考虑了有效波面修正系数e-kT*。
其中:T*——等效吃水,即设计水线下面积与设计水线宽的比值。
2.2 船体水动力系数计算
采用切片法计算式(14)、(15)的水动力系数。参考舰船耐波性基础[12]上的查图谱方法,先得到各切片单位长度的附加质量和阻尼系数,再积分得到水动力系数。
文中采用某隐身船形为例,计算耦合运动方程水动力系数。
3 船舶垂荡与纵摇耦合运动频率散射机制
3.1 垂荡与纵摇耦合运动频率散射概念
文献[11]中提出了遭遇频率散射的概念,本文讨论在垂荡与纵摇耦合运动方程中,通过纵向速度振荡引起的遭遇频率散射机制。
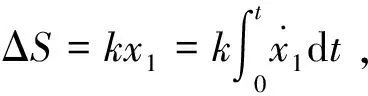
(16)
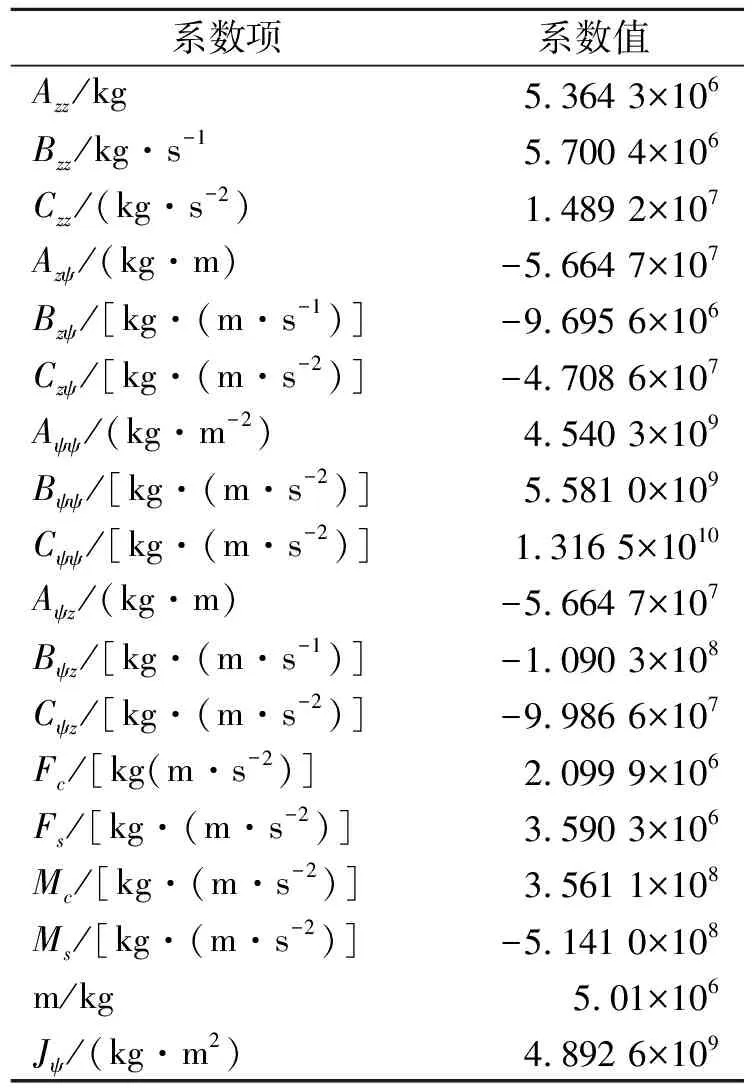
表1 隐身船垂荡与纵摇耦合运动方程系数
将表1中的水动力系数代入式(16),再设定遭遇频率散射强度和散射频率,利用Matlab软件编制程序,可以数值求解该二元二次常微分方程组,可以得到垂荡和纵摇耦合运动规律。
3.2 散射强度对垂荡与纵摇耦合运动的影响
散射频率ωω取常值0.2 s-1,散射强度系数kω从0变化到0.24,即每隔0.08变化一次。kω= 0.16时垂荡与纵摇运动和运动速度的历时曲线见图2。历时曲线中z为垂荡位移,z-dot为垂荡速度,θ为纵摇角度,θ-dot为纵摇角速度。历时曲线由许多幅值不等的振荡周期组成,取历时曲线中所有的振荡周期的幅值组成新的数组。该数组可以反应垂荡与纵摇运动和速度振幅,再计算该数组的最大值和平均值,结果见表2。
根据表2以及图2,可以得到以下规律。
1)随着散射强度系数的增加,垂荡与纵摇运动和速度的振幅最大值曲线均呈现出明显的上、下波动,但波动变化范围不大,在8%以内。
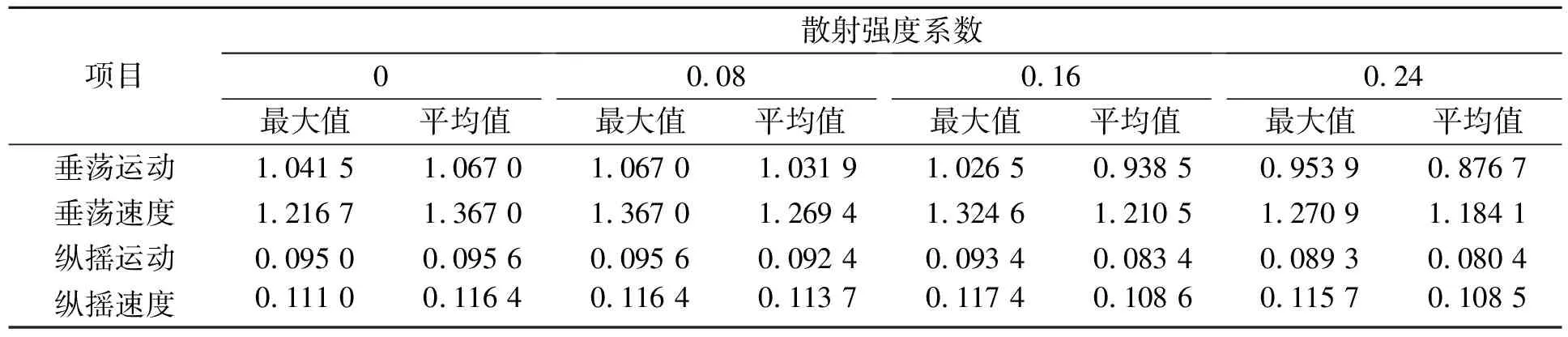
表2 垂荡与纵摇运动和运动速度绝对方差及相对方差随散射强度变化
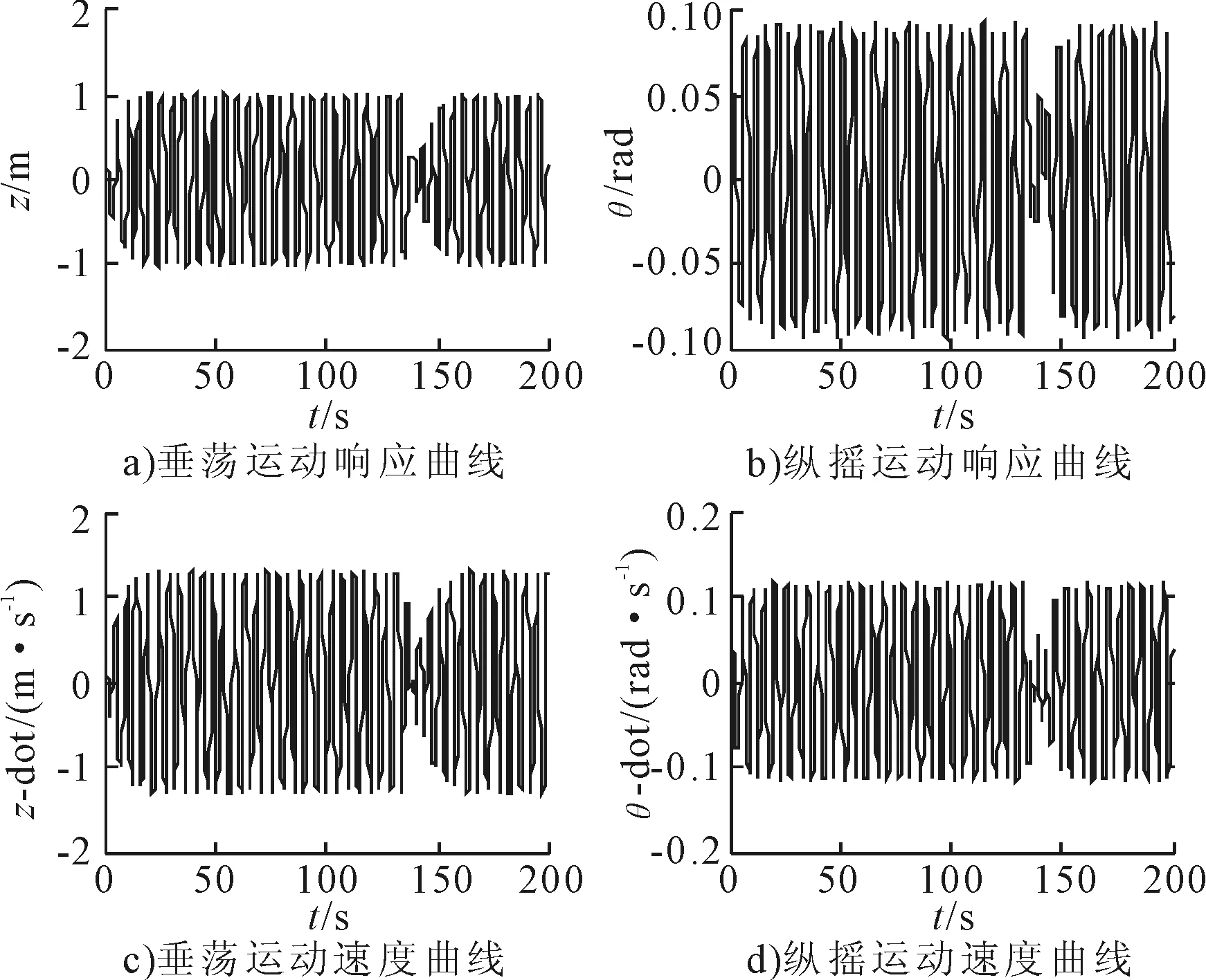
图2 kω=0.16时垂荡和纵摇运动和速度曲线
2)随着散射强度系数的增加,垂荡与纵摇运动的振幅平均值曲线均呈现出不断减小的趋势。在散射强度系数等于0.24时,相比无频率散射时分别降低了18%和16%。垂荡与纵摇速度的振幅平均值曲线也呈现出不断减小的趋势,在散射强度系数等于0.24时,相比无频率散射时分别降低了13%和7%。
3)增大散射强度系数,垂荡与纵摇耦合运动的振幅平均值减小,即耦合运动减弱;垂荡与纵摇耦合运动速度的振幅平均值减小,即耦合运动剧烈程度降低。
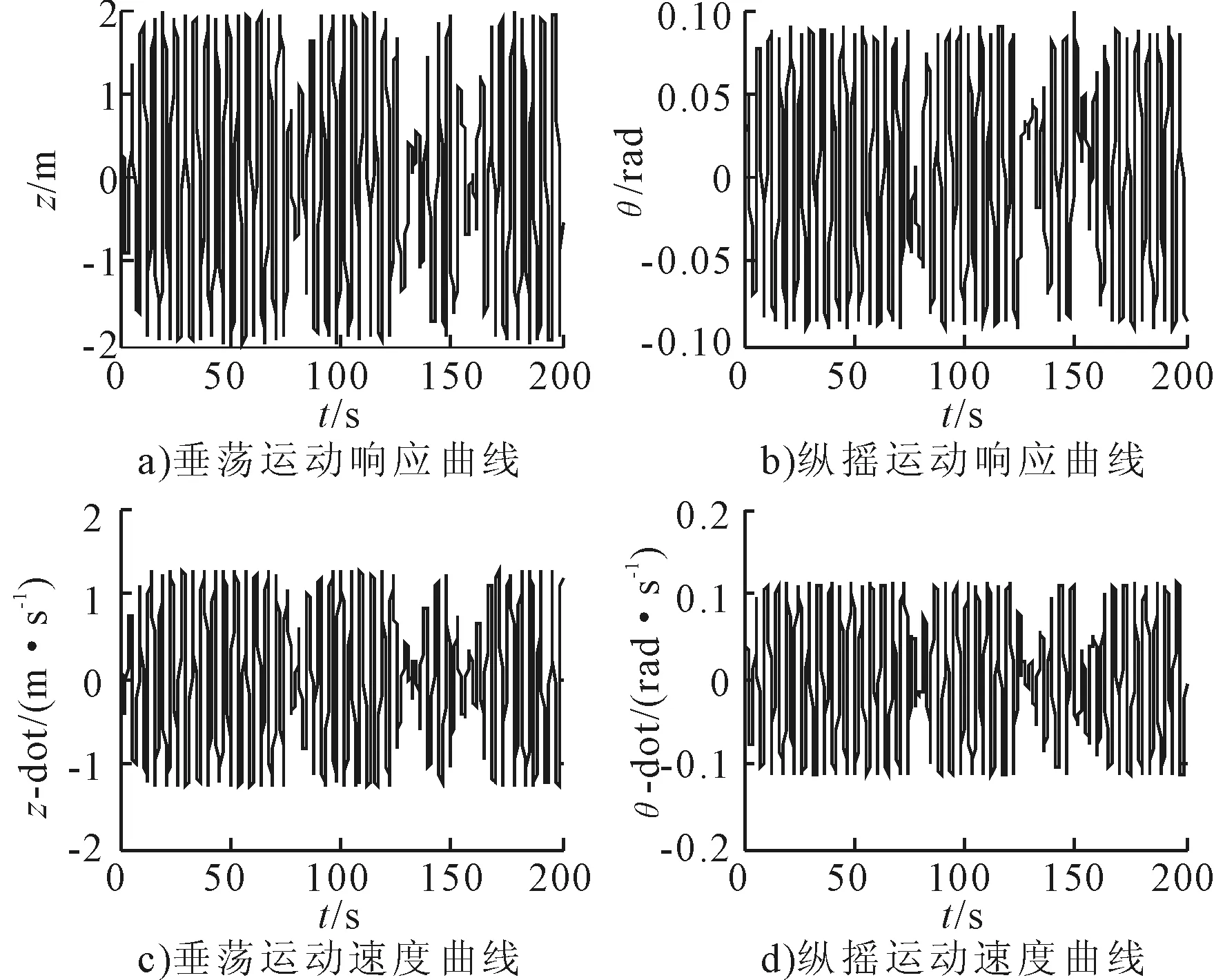
图3 ωω=0.36时垂荡和纵摇运动和速度曲线
3.3 散射频率对垂荡与纵摇耦合运动的影响
散射强度系数kω取常值0.2,散射频率ωω从0变化到0.36 s-1,即每隔0.12 s-1变化一次。ωω= 0.36时垂荡与纵摇运动和运动速度的历时曲线,见图6~9。同样,取历时曲线中所有的振荡周期的幅值组成新的数组,再计算该数组的最大值和平均值,结果见表3。
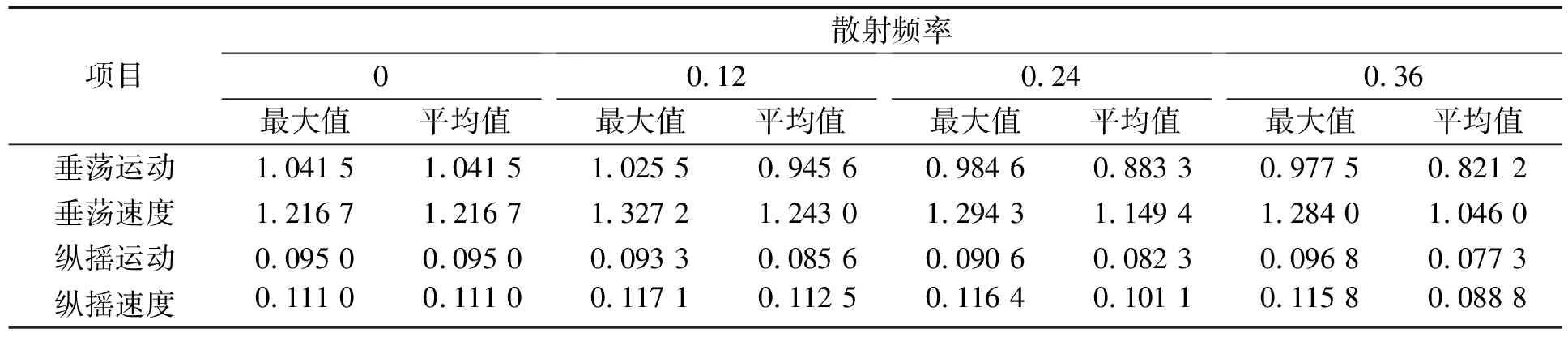
表3 垂荡与纵摇运动和运动速度最大值、平均值及标准差随散射频率变化
根据表3以及图3,可以得出以下规律。
1)随着散射频率的增加,垂荡与纵摇运动和速度的振幅最大值曲线均呈现出明显的上、下波动,但波动变化范围在7%以内。
2)随着散射频率的增加,垂荡与纵摇运动的振幅平均值曲线均呈现出不断减小的趋势。在散射强度系频率等于0.36时,相比无频率散射时分别降低了21%和19%。垂荡与纵摇速度的振幅平均值曲线也呈现出不断减小的趋势,在散射强度系数等于0.36时,相比无频率散射时分别降低了14%和20%。
3)增大散射频率,可以减弱垂荡与纵摇耦合运动和降低耦合运动剧烈程度。
4)散射频率增加,即代表正弦振荡速度的周期减小,这将使历时曲线中的每一个振荡周期减小,在同样的时间段内,将出现更多的完整子振荡,如同振荡周期被压缩了一般。
4 结论
1)散射强度和散射频率的变化将引起垂荡和纵摇耦合运动和速度的振幅最大值上下波动,但波动范围较小,可以近似认为振幅最大值基本不变。
2)散射强度和散射频率的变化将引起垂荡和纵摇耦合运动和速度的振幅平均值的减小,即可以减弱垂荡与纵摇耦合运动和降低耦合运动剧烈程度。
3)从减小船舶摇荡运动的角度考虑,应在振荡速度允许的条件下,尽量选择较大的散射强度系数;在振荡周期允许的条件下,尽量选择较大的散射频率。
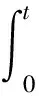
上述关于船舶遭遇频率散射强度和散射频率对纵摇与垂荡耦合运动特性影响分析的结论,尚需今后进一步深入开展数值计算验证。
[1] DAVIDSON K S M. The steering of ships in following
seas[C]∥Proceeding of the 6th International Congress for Applied Mechanics, 1948:554-568.
[2] RYDILL L J. A linear theory for the steered motion of ship in waves[J]. Quarterly Transactions of the Institution of Naval Architects, 1959,101(1):81-112.
[3] EDA H. Steering characteristics of ships in calm water and waves[J]. SNAME, 1965,173:135-177.
[4] EDA H. Direction stability and control of ships in Waves[J]. Journal of Ship Research, 1972,16:205-218.
[5] NONAKAK. On the maneuvering motion of a ship in waves[J]. Transaction of the West-Japan Society of Naval Architects, 1991,80:73-86.
[6] 朱 军,庞永杰,徐玉如.规则波浪中舰船操纵运动计算[J].哈尔滨工程大学学报,2004,25(1):1-5.
[7] 陈俊锋,朱 军,葛义军.规则波浪中舰船操纵与横摇耦合运动模拟及分析[J].舰船科学技术,2009,31(3):46-50.
[8] 朱 军,陈俊锋,葛义军.规则波浪中船舶操纵响应遭遇频率频散概念与机制[J].海军工程大学学报,2010,22(3):7-10.
[9] 陈俊峰,朱 军.规则波浪中舰艇不规则摇荡运动计算分析[J].舰船科学技术,2011,33(1),41-44.
[10] CHEN JUN-FENG, ZHU JUN. Study on the amplitude characteristics of pitch and heave motions for a ship based on frequency scattering[J].Future Intelligent Information Systems,2011(1):157-164.
[11] CHEN JUN-FENG, ZHU JUN. The conception and mechanism of ship frequency scattering due to maneuvering in regular waves[J]. Advanced Materials Research, 2011,180:1248-1253.
[12] 彭英声.舰船耐波性基础[M].北京:国防工业出版社,1989.

