基于网络的水下平台显控系统研究
,,,
(华中科技大学 船舶与海洋工程学院,武汉 430074)
本显控系统是一种新型水下试验平台的重要组成部分,是一种基于网络的分布式系统。本课题研究的水面显控系统是该水下试验平台的数据处理中心和监控显示系统,进行实时显控,并记录试验数据。
该试验平台工作于水下150 m深环境,平台四角由锚固定,每个锚由一台锚泊绞车和一台张紧绞车进行控制收放,绞车由液压马达驱动,进行调平。利用牵引绞车牵引位于平台上的小车,使小车在平台导轨上达到指定速度以完成指定实验。平台模型及显控系统结构见图1、2。


图1 平台模型 图2 显控系统结构
显控系统在功能上来说,分为三个功能模块:网络通信模块、数据处理模块和实时再现仿真模块,功能结构图见图3。

图3 显控系统功能结构
1 系统的设计与实现
1.1 硬件结构
系统主要由主控节点、数据处理节点(工控机2)、实时三维仿真节点(工控机1)、应急控制节点等组成,系统采用基于以太网的分布式结构,由数据图表显示节点控制整个仿真系统的数据接收、处理、存储以及仿真推进,系统结构见图4。
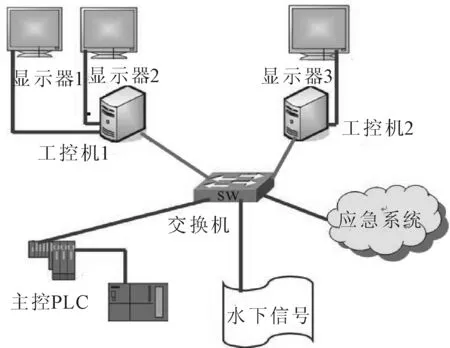
图4 系统网络结构
主控节点(主控PLC)接收水下设备传输上来的信号,并将其数据发送给指定节点。(主控节点的控制作用在这里不做讨论)。
数据处理节点是数据的管理站点,它接收主控制节点传送的数据,并进行数据解析、数据校验、参数处理和数据存储,另外还要对小车和平台的速度等数据进行图表曲线显示,以及为实时三维仿真节点提供仿真数据。实时三维仿真节点主要进行三维建模、实时的三维仿真等。
应急节点是在水下设备不能正常工作的情况下启动应急系统,水下数据将从应急节点传输。
1.2 数据通信
网络通信是本网络显控系统的硬件基础,本系统使用普通的以太网为通信介质,采用标准的TCP/IP协议传输数据。
本系统网络通信采用基于TCP协议的流式套接字,使用Winsock编程最常用的模式:服务器-客户端模式(Server-Client)[1-2],网络通信过程见图5。

图5 Server-Client模式通信过程
1.3 实时数据处理
1.3.1 数据处理流程
实时数据处理是本系统的核心内容,是所有其它工作的数据中心,其工作流程如下。
1)数据处理节点接收到主控节点的数据码字,对其进行数据解析,根据预设定的编码位设置,解析帧类型、帧长等设备和编码信息,以及运动和状态等具体数据。典型小车数据位设置见表1。

表1 小车数据位设置
2)对数据进行滤波,即数据校验。在程序中设置一个计算器count,一旦接收到异常数据,计数器从0开始计数,如果连续异常次数超过5此,也就是说count>5时,有理由认为设备发生了故障,这时必须进行检查。数据校验的程序流程图见图6。

图6 数据校验流程
3)将正确的数据进行存储,供以后查阅。存储的数据中不仅包括实时的小车速度、位置,平台倾角、深度等信息,还包括具体信息数据的发送(或接收)时刻,设备号等。
4)对一些没有直接信号的数据,还须通过计算后一起存储,比如小车加速度,在程序中使用结构体Struct来表示一个设备数据。例如小车的数据结构定义为
Struct Car
{
char carID[8];//小车设备 ID号
char time[20];//时刻
float speed;//瞬时速度
float acceleration//瞬时加速度
float displacement;//位移
int direction;//方向
Coordinate coords;//坐标位置
}
之后,取出数据,对小车、平台等数据进行图表曲线的实时绘制。数据流程图见图7。
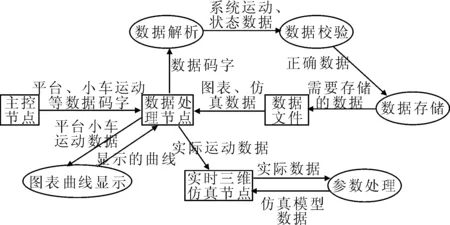
图7 数据处理流程
1.3.2 设计实现
如果将所有的工作放在同一个线程,如果出现上面的情况,将会发生阻塞,发送过来的数据得不到及时的处理,很可能会丢失。
本系统采用多线程技术,创建3个线程:线程1(数据接收线程)负责处理数据的接收;线程2(数据处理线程)负责数据解析、数据存储和发送放;线程3(曲线图表线程)负责从数据区中取数据,以及曲线图表显示,简单的数据流程见图8。

图8 数据处理节点流程
既然用到了多线程技术,必然会涉及到线程的同步问题。使隶属于同一进程的各线程协调一致地工作称为线程的同步[3]。当多个线程同时读写同一份共享资源的时候,可能会引起冲突。当线程1对数据区的写操作和线程2的读操作同时进行时,这时可能会出现读数据错误,可以使用事件(CEvent)来进行线程的同步。
CEvent类提供了对事件的支持。事件是一个允许一个线程在某种情况发生时,唤醒另外一个线程的同步对象[4]。例如在某些网络应用程序中,线程1负责监听通信端口,线程2对接收的数据进行处理。通过使用CEvent类,线程1可以通知线程2何时处理数据。部分程序实现如下。
在线程1的函数中Thead1Func(LPVOID pParam)进行写操作,写完即唤醒读操作:
......
WaitForSingleObject(hEvent.m_hObject,INFINITE);//等待
write();//写入操作
hEvent.SetEvent();//设置为有信号,唤醒读操作
......
在线程2的函数中Thead2Func(LPVOID pParam)进行读操作,开始时即设置为有信号,可以进行写操作:
......
hEvent.SetEvent();//设置为有信号
WaitForSingleObject(hEvent.m_hObject,INFINITE);//等待
read();//写入操作
hEvent.SetEvent();//设置为有信号
......
同样,线程2与线程3之间也可以使用这种同步处理。
1.4 实时三维仿真
1.4.1 三维模型动画
由于OpenGL没有提供高级命令函数来定义复杂的三维模型[5],本系统利用3DSMax建立三维立体模型。在3DSMax中,将所建立的几何模型保存为3DS数据格式,然后导入到软件系统中。需要注意的是3DS数据格式只能保存和转换几何信息,而色彩、材质等信息可能会在转换时丢失[6]。
动画是由一帧帧有序的图像连续播放形成的,而每帧都是由一些特定图形对象绘制在屏幕上形成的[7]。因此要形成动画,必须选好每一帧的时间间隔,以及模型在每一帧之间的运动“间隙”(包括位移、角度等)。
理解动画的原理对后面的参数处理将有很大的影响,因为三维仿真中,模型的运动必须考虑到时间间隔和运动“间隙”。
1.4.2 数值处理
读取到解析后的数据后,数据还不能直接用于三维仿真。读取的数据是真实物体的运动数据,必须经过参数处理,转化为三位模型数据,才能运用于三维仿真中。
以小车为例,设小车轨道实际长为Lrl,模型中小车导轨长为Lml,以导轨最左端为坐标原点,设实际导轨上某坐标数值为Lrc,模型中导轨相应的坐标值为Lmc,则有
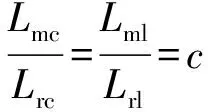
(1)
由式(1)可得模型坐标值Lmc=Lrl·c。
这样可以轻松地用小车的真实坐标值,乘以比例值c,得到三位仿真位置坐标值。速度、加速度等涉及物理量也可以这样处理。
但是角度的处理就不能这样乘以一个比例值,角度值不需要比例值。实际上是利用相似性原理,将实体大小缩放成模型的大小,而角度是不变的(类比相似三角形)。
模型的比例值并不一定全都一样,为增加模型的真实感,以及便于显示观察,某些模型比例值会作适当调整。如为便于观察,锚的比例值Cm会比平台的大,但从仿真的真实感考虑,锚的深度、下放和上拉的速度,计算时将使用平台模型的比例值。这一点要特别注意。
1.4.3 时钟处理
对于动画演进,实际上是利用程序在间隔时间内重绘每个坐标点[8],时间间隔是靠定时器中断产生的,在代码中可由函数SetTimer()设置一个系统时钟周期Tm(前述时间间隔)。
接收到的数据也有一个时钟周期Tr(水下数据发送周期),如果Tr<1/24(人眼视觉停留时间),一般取仿真时钟周期Tm=Tr即可,此时可以保证动画的连续性。但是本系统水下有多个控制器和传感器,它们发送数据的时钟周期并不统一,取Tm=Trmin,那么对于Tr>Tm的设备数据须进行特殊处理。
当设备Tr>Tm时,设备的数据没有出现在时刻N·Tm,这时会出现“数据真空”问题。那么必须使用一个比较合理的算法,利用已有的数据,近视地推算出N·Tm时刻的位置数据。
为此,设计比较可行的算法——中点逼近法。
在一段时间内,物体有数据传输过来,设从时刻t1开始,其数据传输时钟周期为Tr,那么,在时刻t1,t1+Tr,t1+2·Tr…t1+i·Tr…,程序中可以读到数据Mr0,Mr1,Mr2,…,Mri,…。
将时刻简化,见图9,

图9 中点逼近法
现在的问题是,已知读取到了tr0,tr1,tr2,…,tri-1,tri,时刻的数据Mr0,Mr1,Mr2,…,Mri,如何求出tmj时刻的数据Mrj。不断取中点,使用中点不断地逼近,直到某两点的中点时刻为tmj,即认为该点时刻数据为Mrj。
1)如果tri=tmj,则有Mrj=Mri,算法结束;否则执行2)。
2)根据Mri-1,Mri求出Mri+1,tri是[tri-1,tri+1]的中点,取Mri为时间段[tri-1,tri+1]的平均值,设有
2·Mri=Mri-1+Mri+1
(2)
则有Mri+1=2·Mri-Mri-1。
再取[tri,tri+1]的中点时刻tM0,近似计算该时刻数据M0=(Mri+1+Mri)/2,如果tM0=tmj,则有Mrj=M0,算法结束。
3)否则,如果tM0>tmj,利用[tri,tM0]的中点,以及Mri和M0重复步骤2)(将tM0赋值给tri+1,将M0赋值给Mri+1);
4)否则,如果tM0 注意: ①传输时钟开始时刻对应的第一个程序时钟为仿真的开始,也就是说程序开始的时刻要早于传输;同样,程序时钟结尾时刻要晚于传输。 式中:S——位移或角度; Si-1——已经接受到的数据; v(vi-1和vi)——速度或角速度。 算法的可行性说明。 1)平台和小车等的运动过程是一个比较缓慢的过程,一般来说,在某一段时间内可以近似地看成是线性运动,在这种情况下,用中点逼近比较合理; 2)程序时钟周期取各数据传输的最小值,每一个周期非常短,那么数据变化也非常小,用中点逼近误差很小。 以小车运动为例,选取小车数据传输周期为Tr=0.037 5 s,程序周期为Tm=0.025 s。小车的运动规律见图10。 图10 小车运动规律 试验中,网络传输的数据经过解析和滤波之后的数据如下,选取t∈(5,7.348)时间段(加速度开始匀速减小)中部分,以t=5.0 s为开始时刻,获取到的数据只在N·Tr时刻,见表2。在三维仿真时,在时刻N·Tm的仿真数据见表3。 表2 实验传输数据 表3 仿真数据 表3中,实际数据是根据小车运动规律(图10所示)算出的小车的理想运动数据;推算位移是根据公式(3)算出的三维仿真中小车位移量。 从结果可以看出,网络传输的数据较为稳定,数据处理各线程工作协调,能较好地保证数据传输和处理的同步。从表3可以看出,“中点逼近”得出的位移量和理想数据基本上是一致的,其误差非常小,结果非常理想。 1)针对控制器在水下串口通信速率不高的特点,采用普通以太网的TCP/IP通信网络,不仅提高了通信速率,而且大大增强了通信的稳定性。 2)利用半物理三维仿真动画,能流畅地实时地从水面观测水下工作状态。 3)使用中点逼近法,能比较理想地解决程序时钟和数据传输时钟不一致而产生的“数据真空”问题。 本系统经过了多次船池模拟实验,实验证明,数据处理和接收稳定可靠,三维仿真实时性较高,该研究可以较好地实现显控系统的要求。但其中也有欠缺,数据处理中的线程可以考虑使用线程池技术,参数处理中的时钟处理算法原理上比较粗略,这些也是今后的研究内容。 [1] TANENBAUM A S.计算机网络[M].潘爱民,译.北京:清华大学出版社,2004. [2] 汪 翔,袁 辉.Visual C++实践与提高——网络编程篇[M].北京:中国铁路出版社,2001. [3] 戴大蒙.基于非阻塞式Winsock的多线程网络通信机制[J].计算机工程,2006,32(6):137-138. [4] 郭羽成.三维视景仿真中面向客户端的网络同步模型研究[D].武汉:武汉理工大学,2006. [5] 孙 卿.基于OpenGL的卫星运行仿真[D].武汉:华中科技大学,2004. [6] 葛 翔.基于OpenGL的三维建筑仿真与漫游技术研究[D].武汉:武汉理工大学,2006. [7] 陈 勇.仿生机器人运动形态的三维动态仿真[D].长春:吉林大学大学,2005. [8] 刘 升,王行愚,游晓明.基于VC++的OpenGL三维动画仿真及场景漫游的实现[J].计算机工程与设计,2006,27(17):3235-3238.
2 实验结果



3 结论

