基于层次分析法的机械振源贡献研究

，， ，

(1.海军工程大学 船舶与动力工程学院，武汉 430033;2.海军装备部舰船技术保障部，北京 100841)

在噪声控制中，在噪声源上控制噪声是最根本和最有效的方法。为了在噪声源上控制噪声，必须首先找出主要的噪声源。在同一个声学环境中，往往存在多个噪声源。只有找到主要的噪声源，并了解其特性，才能有针对性地采取有效措施进行噪声控制。船舶中机械设备数目众多，机械设备的噪声耦合严重，噪声传递路径复杂，采用传统的方法无法进行噪声源识别和分离。层次分析法(analytic hierarchy process， AHP)是对一些较为复杂、模糊的问题作出决策的简易方法，它特别适用于那些难于完全定量分析的问题[1-2]。本文将层次分析方法应用于船舶机械振源识别与贡献量排序，将复杂问题层次化、数量化，能够确定系统各主要噪声源的主次顺序，为进一步的工程应用提供依据。

1 层次分析法应用于噪声源识别

根据层次分析理论[3-6]，结合噪声源特点，建立具有三个层次的结构图：目标层为各噪声源的贡献量排序；中间层为频率层，层中各因素为由外部噪声评价点的噪声频谱确定的峰值频率或频段；最低层为噪声源层。然后，由最高层到最低层逐层计算各层次所有因素对于目标层相对重要性的排序权值，声源的权值越大，表明该声源对评价点噪声的影响越大，由此可得到声源的诊断结果，见图1。

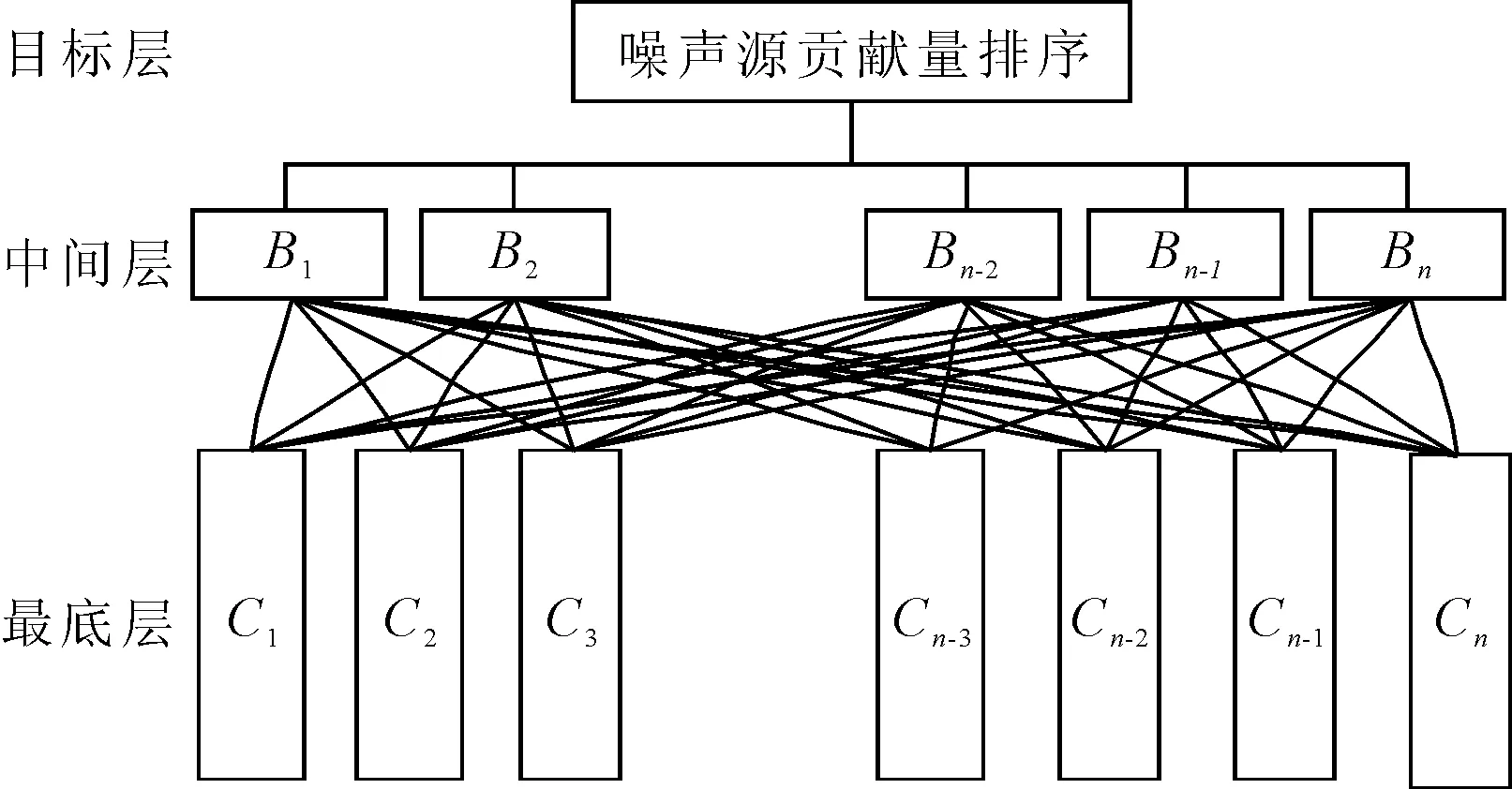
图1 层次结构示意

2 噪声源识别仿真研究

采用一组频率相互耦合的信号作为输入，将这组信号的叠加结果作为输出信号，以模拟一个多输入单输出系统，再利用基于偏相干方法的层次分析对仿真系统中输入对输出的贡献量进行排序。

2.1 仿真参数

选取一组频率作为输入信号的频率。

f1=100 Hz，f2=600 Hz，f3=350 Hz，

f4=850 Hz，f5=700 Hz，f6=1 000 Hz。

采样频率为4 096 Hz，采样长度为4 096点。

2.2 仿真工况

取2.1中所列的仿真频率进行组合，作为输入信号的频率，分别产生4个合成信号x1，x2，x3，x4作为输入，使用4个输入信号的合成作为输出y，组成多输入单输出系统，系统框图见图2。

2.3 信号表达式

为模拟真实测量工况，在输入信号中加入随机相位φ=randn(1, length(t))，并在输入和输出信号中添加噪声，信号表达式如下。

图2 多输入单输出系统示意

x1=1.5sin(2πf1t+φ1)+2.4sin(2πf2t+φ2)+1.4sin(2πf3t+φ2)+0.5randn(1,length(t));

x2=2.5sin(2πf1t+φ3)+3.1sin(2πf2t+φ4)+2.4sin(2πf4t+φ2)+0.7randn(1,length(t));

x3=1.6sin(2πf2t+φ5)+2.3sin(2πf3t+φ6)+2.4sin(2πf5t+φ2)+0.9randn(1,length(t));

x4=0.9sin(2πf3t+φ7)+1.3sin(2πf4t+φ8)+1.6sin(2πf6t+φ2)+0.3randn(1,length(t));

yt=x1+x2+x3+x4+0.2randn(1,length(t))。

3 层次分析模型

利用所获得的偏相干分析结果进行层次分析，建立层次分析模型。根据层次分析基本原理及仿真系统的特点，建立层次分析模型(见图3)，目标层为输入信号对输出信号的贡献量排序结果，准则层取输出信号中所有仿真频率对应的能量，指标层为在每个仿真频率下4个输入信号对输出信号的偏相干函数值。

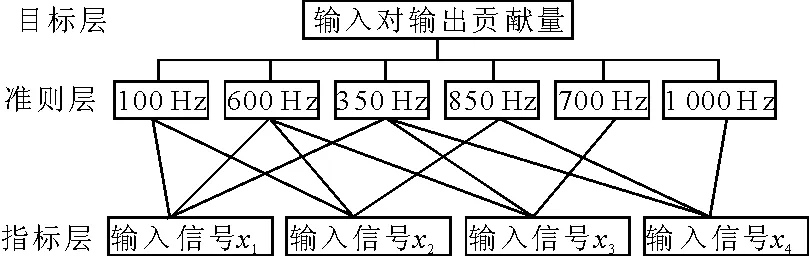
图3 层析分析模型

4 贡献量排序结果

使用两两比较的方法确定每层中的元素对于其子指标的判断矩阵。首先比较准则层中每个频率的计算结果，获得准则层判断矩阵，根据判断矩阵计算准则层中每个频率下的能量在输出信号中的权重，见表1。

表1 准则层权重

再取准则层中的每个分析频率，计算比较该频率下4个输入信号在该频率下对输出信号的偏相干函数值，获得4个输入在此频率下的判断矩阵。而后根据所求得的判断矩阵计算4个输入对应于每个分析频率的权重向量见表2。

表2 四个输入信号对于各分析频率的权重结果

获得各层的权重结果后，计算4个输入信号对于总目标的权重值。结果见表3。

表3 四个输入信号对于总目标的权重值

5 实验研究

实验以双层环肋圆柱壳模型为对象在消声水池中进行，见图4。

图4 双层环肋圆柱壳模型

水池尺寸为16 m×8 m×8 m，6面消声。模型内壳上布放三台激振器，以模拟内部多个设备同时开启的状态，激振器2位于模型中部，激振器1、3位置对称，三台激振器等间隔布放，见图5。

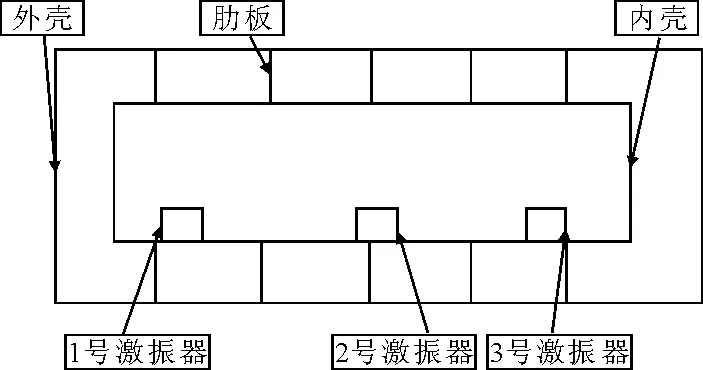
图5 双层模型激振器位置

同时开启多台激振器，以模拟船舶内部多个设备同时开启的状态，采集设备周围的振动数据和模型外部水声数据进行分析。然后以分布运转法验证比较结果。

当激励1为频率500 Hz的sinc信号，激励2频率1 000 Hz的sinc信号，激励3频率3 000 Hz的单频信号，功放幅值均为46 V。实验结果见图6。

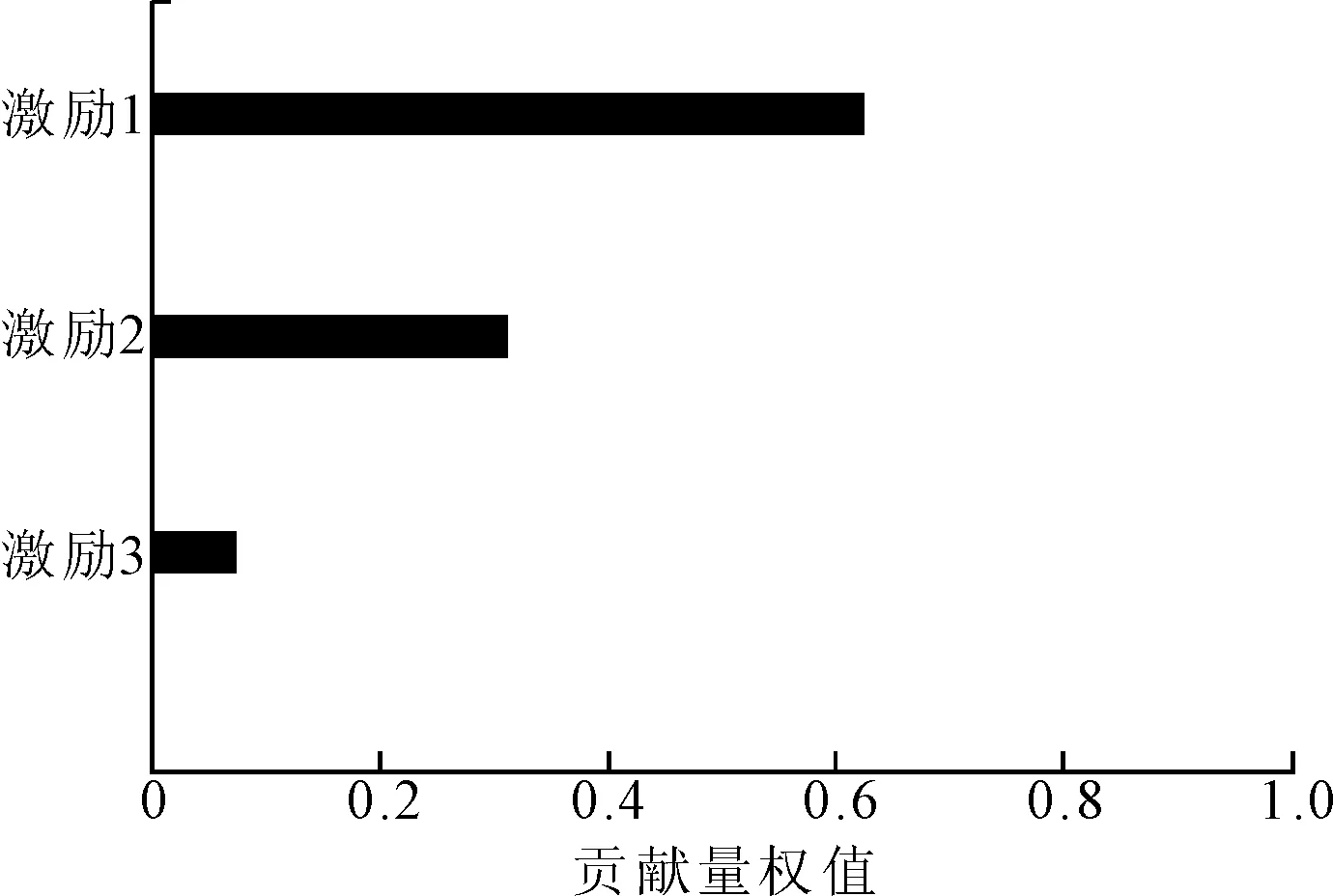
图6 层次分析试验结果

分别开启每台激振器，并采集模型外部水声数据，应用分部运转法获得各激振器单独激励时外部辐射声场的大小，结果见图7。与层次分析法结果基本一致。

6 结论

仿真和试验说明，层次分析方法应用于船舶机械振源识别与贡献量排序，将复杂问题层次化、数量化，能够确定系统各主要噪声源的主次顺序，可为下一步工程应用提供依据和指导。

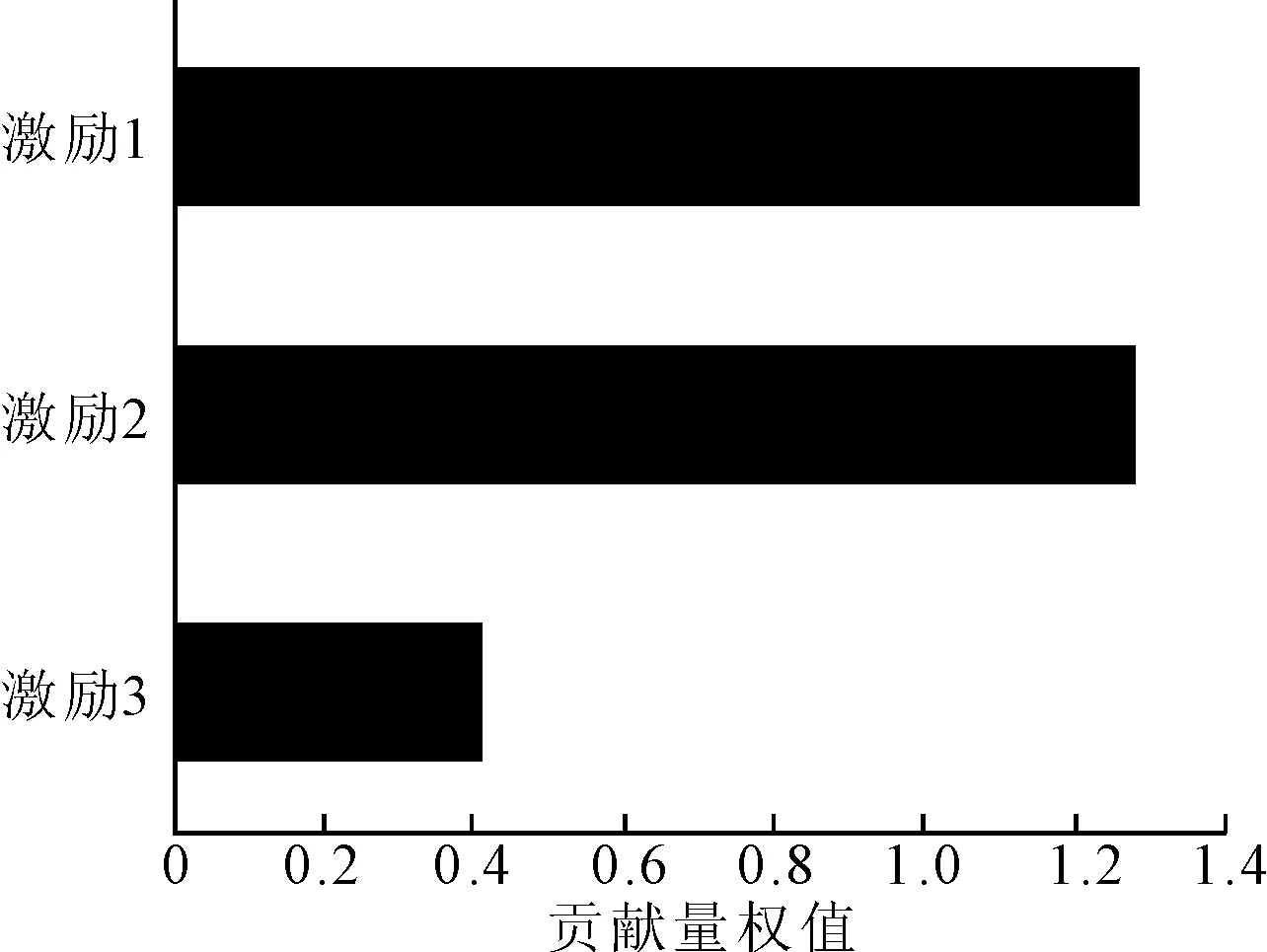
图7 分部运转法结果

[1] 赵焕臣，许树柏，和金生.层次分析法:一种简易的新决策方法[M].北京:科学出版社,1986.

[2] 刘新宪，朱道立.选择与判断:AHP决策[M].上海:上海科学普及出版社,1990.

[3] 王莲芬，许树柏.层次分析法引论[M].北京:中国人民大学出版社,1990.

[4] 吴殿廷，李东方.层次分析法的不足及其改进的途径[J].北京师范大学学报(自然科学版),2004(2):264-268.

[5] 常建娥，蒋太立.层次分析法确定权重的研究[J].武汉理工大学学报:信息与管理工程版,2007(1):153-156.

[6] 贝达特 J S，皮尔索A G(著).相关分析和谱分析的工程应用[M].凌福根,译.北京:国防工业出版社,1983.