施工期边坡稳定性分析中适用的强度

殷博，姜昱，郭玉彬，刘丹忠，李卫

（1.天津市建筑设计院，天津 300074；2.辽宁凌云装饰装修有限公司，辽宁 锦州 121001；3.中交天津港湾工程研究院有限公司，港口岩土工程技术交通行业重点实验室，天津市港口岩土工程技术重点实验室，天津 300222；4.长江武汉航道工程局，湖北 武汉 430014）

0 引言

众所周知，在边坡工程设计中，其稳定性分析是最主要的工作之一。由于事关工程设计的成败，往往是工程师们最关心的问题。在边坡稳定性分析中，已有很多较为成熟的计算方法，且这些方法已经编成了很多方便应用的计算软件；但地基土的土性指标的确定，特别是土体强度指标的确定，常常成为分析计算过程中的关键问题。

工程经验告诉我们，发生滑坡的情况多是具有饱和软土的地基，且多是发生在包括工程主体完成时的工程施工期[1]。对饱和软土地基，在工程施工过程的不同阶段，地基土的强度或强度指标是不同的，尤其是常采用各种方法进行地基处理（如打设了排水通道），地基土固结作用非常显著，对地基土强度的影响很大，其强度指标的确定是边坡工程设计中的主要问题之一，也是土力学界经常研究和讨论的问题[1-3]，更是工程界关心的问题。工程师们在工程中如何根据不同的情况，采用正确的强度指标，是边坡工程设计中至关重要的问题。

目前，施工期地基土强度的确定方法很多，分析不同方法确定强度的合理性及其计算效果，提出与施工期计算状况更为一致的强度确定方法，是一项有重要工程意义的工作。

1 采用不同强度指标时的计算效果差别

1．1 不同强度指标计算公式

对饱和土地基上的边坡工程，如果饱和土体已经完全固结（如固结度已达95%以上），采用固结快剪强度指标；如果饱和土体完全没有固结（如固结度小于5%）采用十字板剪、直剪快剪等不排水剪强度指标，进行稳定性计算都是没有问题的。

当饱和土体已经完成了部分固结，比如打设了排水通道（塑料板），可以有以下几种计算方法：一是采用固结快剪强度指标，并考虑土体的孔隙水应力；二是采用十字板剪、直剪快剪等不排水剪强度指标，并考虑因土体固结产生的强度增长。

在工程主体完成时，这几种计算方法均是可以应用的，这里以简单条分法为例，讨论各种计算方法的强度差别；相应的抗滑力矩计算公式[4]如下（计算图示见图1）。

图1 计算示意图

方法一：采用固结快剪强度指标，并考虑土体的固结度。抗滑力矩MR的计算公式为：

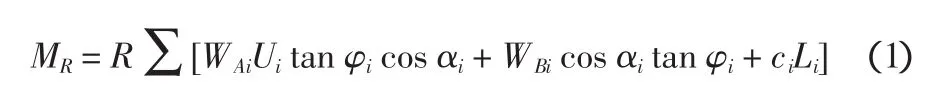
式中：WAi为边坡表面荷载和施工过程中土条宽度内填土重力，kN/m；WBi为滑动面以上土条宽度内原地基土重力，kN/m；Ui为滑动面上的固结度，当滑动面通过原地基表面以上的填土时，Ui=1.0；φi、ci分别为滑动面上的固结快剪内摩擦角，（°）、黏聚力，kPa；αi为滑弧切线与水平线夹角，（°）；Li为土条的滑弧弧长，m。以上参数均是第i土条上的值。

方法二：采用十字板剪强度，并考虑因土体固结产生的强度增长。抗滑力矩MR的计算公式为：

式中：σzi为填土重力产生的垂直附加应力，kPa；bi为土条宽度；Sui为滑动面上的十字板剪强度。

当滑动面通过原地基表面以上的填土时，Ui=1.0，σzi应改为 WAi，Sui应改为 ci。

方法三：采用直剪快剪强度，并考虑因土体固结产生的强度增长。抗滑力矩MR的计算公式为：式中：φqi、cqi分别为滑动面上的直剪快剪内摩擦角，（°）、黏聚力，kPa。

当滑动面通过原地基表面以上的填土时，Ui=1.0，σzi应改为 WAi，cqi应改为 ci。

当然，还可以采用三轴试验得出的强度指标计算，这里就不一一列举了。

1．2 不同强度指标计算效果分析

由计算公式可见，上述三种计算方法均考虑了原地基表面以上填土对应的强度，及原地基表面以上的填土重力对地基土固结过程的影响，只是计算点上垂直力考虑的方法不同：方法一按土条重力考虑，方法二、三按垂直附加应力考虑；这一差别后面专门讨论。

各种计算方法的主要差别是原地基土所采用的强度，如果固结快剪强度指标是地基土完全固结后的强度指标；十字板剪强度、直剪快剪强度是在获取其强度时，地基土在自重条件下已经完成部分固结条件下的强度指标。则：

方法一采用的是地基土完全固结后土条宽度内的总强度WBicosαitanφi+ciL。显然，除非地基土已经完全固结，否则就是采用了较计算状况偏大的强度，使得计算的安全系数偏大，是一种偏于不安全的计算方法。

方法二采用的是地基土在施工期间完全没有固结的土条宽度内的总强度SuiLi。这是一种只考虑了地基表面以上的填土重力对地基土固结作用，没有考虑施工期间地基土在自重条件下固结作用的计算方法。除非施工期间地基土在自重条件下完全没有固结，否则就是采用了较计算状况偏小的强度，使得计算的安全系数偏小，是一种偏于安全的计算方法。至少对打设了排水通道的情况是这样的。

方法三采用的强度是由两部分组成：一是地基土在施工期间完全没有固结的土条宽度内的总强度WBicosαitanφqi+cqiLi；二是原地基表面以上的填土所产生的强度WAicosαitanφqi。这也是一种只考虑了地基表面以上的填土重力对地基土固结作用，没有考虑施工期间地基土在自重条件下固结作用的计算方法。但对地基表面以上填土重力产生的强度增加了WAicosαitanφqi。

对第一部分强度，是必须要计入的，这是没有疑义的。

第二部分强度是在认为在填土重力对地基土固结作用很快就达到了这一强度的条件下采用的。如果不计入，也是一种只考虑了地基表面以上的填土重力对地基土固结作用，没有考虑施工期间地基土在自重条件下固结作用的计算方法。如果计入，在Ui较小且φqi较小的情况下，应当是没有问题的；但当在Ui较大或φqi较大的情况下，就有可能采用了较计算状况偏大的强度，是一种偏于不安全的计算方法。

所以，方法三是一种半理论半经验的计算方法。

尽管上述方法已在工程中广泛应用，且已被写入有关规范[4]，但由于没有考虑施工期间地基土在自重条件下的固结作用；对饱和土体已经完成了部分固结的情况，以上计算方法的强度均不是与计算状况相一致的强度。如果各种计算方法选用的控制安全系数相同（如文献 [3]对方法一、二采用相同的抗力分项系数，而方法三要求抗力分项系数按经验确定），则其对应的工程安全度是不同的。

2 考虑了地基土在自重条件下固结作用的强度

施工期地基土强度的确定方法很多，除上述方法外，还有综合考虑施工期间地基土固结作用的强度确定方法，如：

直剪试验：

三轴试验：

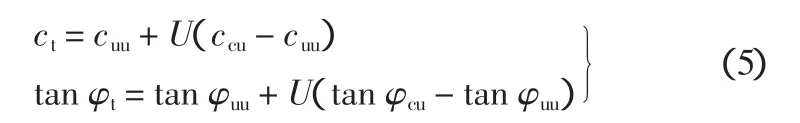
式中：ct、φt分别为考虑地基土固结作用的黏聚力，kPa、内摩擦角，（°）；ccq、φcq分别为直剪固结快剪的黏聚力，kPa、内摩擦角，（°）；cuu、φuu分别为三轴不固结不排水试验的黏聚力，kPa、内摩擦角，（°）；ccu、φcu分别为三轴固结不排水试验的黏聚力，kPa、内摩擦角，（°）。

由式（4） 容易看出，该方法认为：地基土在施工期间完全没有固结时，其强度指标是直剪快剪强度；随着固结度的增加，强度指标随固结度成线性关系逐渐增大，当完全固结时，其强度指标为固结快剪强度。式（5） 的力学意义也是类似的。

将式（4）代入简单条分法的抗滑力矩计算公式，得：

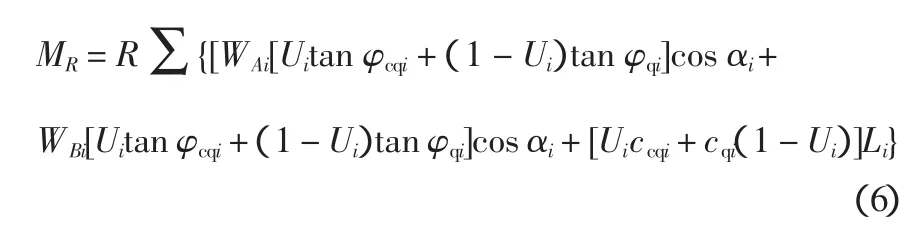
按目前工程中的应用情况，其中的WAiUitanφcqi也可以改为通常的强度增长计算公式σziUitanφcqibi。

按式（6） 计算时，不但考虑了地基表面以上的填土重力对地基土的固结作用，也考虑了施工期间地基土在自重条件下固结作用。与前述的方法相比，这一计算方法采用的强度更合理一些。

需要指出的是该方法有一个前提条件：施工期间地基土在自重条件下的固结度与填土重力对地基土的固结度是相同的。显然，这与工程实际情况不相吻合，不能不说是该方法的一个不完善之处。

3 建议采用的强度

实际上，填土重力是施工过程逐渐增加的，与自重条件下的固结过程是不同的；另外两者的初始孔隙水压力也是不同的，应按不同的初始孔隙水压力计算固结度。所以，两者的固结度是不同的。另外，尽管施工过程逐渐增加的填土重力可以是分级加荷的，但可以按多级加荷的平均固结度应用；而地基土在自重条件下固结度不宜与填土重力的固结度一起应用。因为，地基土在自重条件下固结作用，与填土重力对地基土的固结作用没有关系；例如，地基土的凝聚力就与填土重力对地基土的固结作用无关。

按现有的固结度计算方法，完全能够分别计算填土重力对地基土的固结度和地基土在自重条件下的固结度。这样就可以分别计算填土重力固结作用产生的强度和地基土自重固结作用产生的强度，并按以下公式确定强度指标：

式中：φA为考虑了填土重力固结作用的内摩擦角，（°）；UA为对应于填土重力的固结度；cB、φB分别为考虑了地基土自重固结作用的黏聚力，kPa、内摩擦角，（°）；UB为对应于地基土自重的固结度。

式（7）的强度是与施工期计算状况更为一致的强度，建议采用按这一方法确定的强度进行施工期稳定性计算。

4 填土的土条重力和垂直附加应力的强度分析

前面看到，填土产生的滑动面上一点的垂直力，有两种确定方法：一是单位宽度的土条重力WAi/bi，二是垂直附加应力σzi。由内摩擦角产生的强度分别为WAiUitanφi/bi、σziUitanφi，两者存在一定差别。一般说，按WAiUitanφi/bi计算的安全系数要略小一些，按σziUitanφi计算的安全系数要略大一些。问题是两种方法确定的强度何者更合理呢？这需要从以下两个方面来分析。

单纯从强度方面看。对地基中任意一点的垂直应力，σz是按弹性理论计算的，WAi/bi是按土条重力计算的；相比之下，地基中一点的真实垂直应力可能会更接近于垂直附加应力σzi，从这一方面看，σziUitanφcqi计算地基土一点的强度增长值，可能是合理的。

从边坡稳定性分析方法方面看，岩土工程的稳定性分析应采用极限状态设计原则；符合极限状态设计原则的应力状态不是由弹性理论确定的应力状态，而应是土体最可能发生剪切破坏的极限应力状态[5]。以简单条分法为例，抗滑力矩计算公式为：

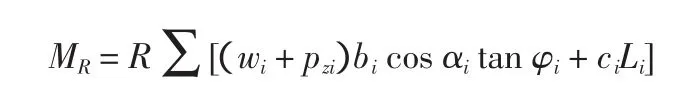
式中：wi=Σγihi，为单位宽度内土条重力；pzi为边坡表面的垂直应力。

显然，地基土一点由内摩擦角产生的强度为（wi+pzi）tanφi。与按WAitanφi/bi计算滑动面上一点的强度是一致的，而与弹性理论确定的垂直附加应力没有任何关系。

所以，从这一方面看，按WAiUitanφi/bi计算地基土一点的强度增长值与边坡稳定性分析方法是一致的，也是合理的。

综合前述的两方面，采用垂直附加应力σzi计算强度时，强度按弹性理论确定的应力状态考虑，不符合极限状态设计原则；稳定性分析方法按极限应力状态考虑，符合极限状态设计原则。采用单位宽度的土条重力WAi/bi计算强度时，强度和稳定性分析方法均按极限应力状态考虑，符合极限状态设计原则。因为极限状态设计原则是岩土工程的稳定性分析应采用的基本原则，按小道理服从大道理的思路，采用单位宽度的土条重力WAi/bi计算强度更为合理。

5 结语

1） 采用固结快剪强度指标，并考虑土体的固结度的计算方法，在地基土没有完全固结时，是采用了较计算状况偏大的强度，是一种偏于不安全的计算方法。

2） 采用十字板剪强度，并考虑因土体固结产生强度增长的计算方法，没有考虑施工期间地基土在自重条件下固结作用，是一种偏于安全的计算方法。

3） 采用直剪快剪强度指标，并考虑因土体固结产生强度增长的计算方法，是一种半理论半经验的计算方法；在固结度Ui较大或内摩擦角φqi较大的情况下，就有可能采用了较计算状况偏大的强度，使其成为一种偏于不安全的计算方法。

4） 施工期的稳定性分析所采用的强度，除应考虑施工过程的填土对地基的固结作用，还应考虑施工期间地基土在自重条件下的固结作用。建议分别考虑这两者的固结作用，并采用按本文公式（7）计算的强度。

5） 采用垂直附加应力σzi计算强度时，不符合稳定性分析方法的应力状态应是极限应力状态的极限状态设计原则；采用单位宽度的土条重力计算强度是更为合理的。

[1]魏汝龙.软黏土的强度和变形[M].北京：人民交通出版社，1987.

[2] 黄文熙.土的工程性质[M].北京：水利水电出版社，1983.

[3] 侯晋芳，刘爱民，闫澍旺，孙万禾.施工期软土边坡稳定分析中抗剪强度指标的确定方法[J].水运工程，2009（12）：178-181.

[4]JTS147-1—2010，港口工程地基规范[S].

[5] 黄传志.土体极限分析理论与应用[M].北京：人民交通出版社，2007.