矩估计法的理论注释

范 光，李广明

（1.十堰职业技术学院公共课部湖北十堰442000；2.丹江口实验中学湖北丹江口）

估计理论是数理统计学的重要内容之一，随机变量 的数字特征同它的概率分布中的参数有一定关系，因而，对数字特征的估计问题，称之为参数的估计问题。

矩法估计量：设总体ξ的分布函数F（x；θ1，…，θl）中有l个未知参数，假定总体ξ的l阶原点矩E（ξl）存在，并记

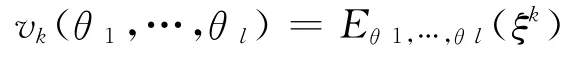
（k＝1，2，…，l），由下列方程组

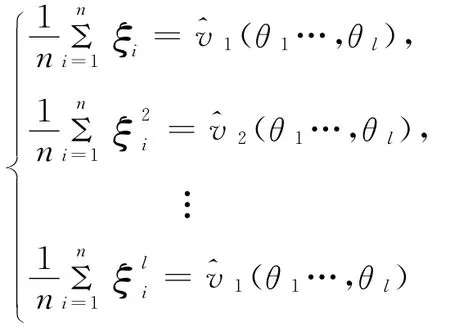
对总体ξ进行n次重复的、独立的观察，得到总体ξ的一个简单随机样本ξ1，ξ2，…，ξn，这n个随机变量相互独立，并且与总体ξ服从相同的分布。

定义1 设ξ1，ξ2，…，ξn是n个随机变量，Fξ1，ξ2，…，ξn（x1，x2，…，xn）及Fξi（xi）分别为（ξ1，ξ2，…，ξn），ξi（i ＝ 1，2，…，n）的 分 布 函 数， 若 对 任 意 实 数 x1，x2，…，xn， 有 Fξ1，ξ2，…，ξn（x1，x2，…，xn）＝Fξ1（x1）Fξ2（x2）…Fξn（xn）则称ξ1，ξ2，…，ξn是相互独立的［1］133。

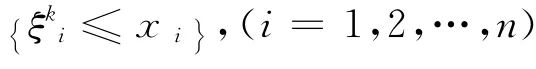
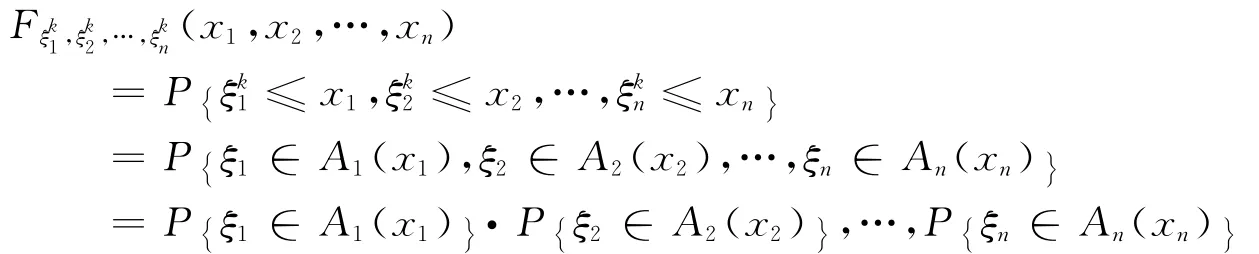
由ξ1，ξ2，…，ξn的独立性可知根据定义1，ξk1，ξk2，…，ξkn相互独立。

定理2 （辛钦定理）［2］对于独立同分布随机变量序列ξ1，ξ2，…，ξn，…如果数学期望Eξi＝μ（i＝1，2，…）存在，则

定义2 设ξ1，ξ2，…，ξn，…为一随机变量序列，若对于任意S个随机变量ξi1，ξi2，…，ξin，…相互独立，则称随机变量序列ξ1，ξ2，…，ξn，…是相互独立的随机变量序列［1］133。

显然，如果ξi与ξ同分布，那么与ξk同分布。

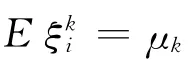
其次，

因此，样本k阶原点矩是总体k阶原点矩μk的无偏估计量［3］。

综合以上，得到矩估计法：

设总体ξ的分布中含有未知参数θ1，θ2，…，θk，ξ1，ξ2，…，ξn是来自总体ξ的一个样本，取样本矩作为总体矩的估计量，注意到总体矩是未知参数的函数，有

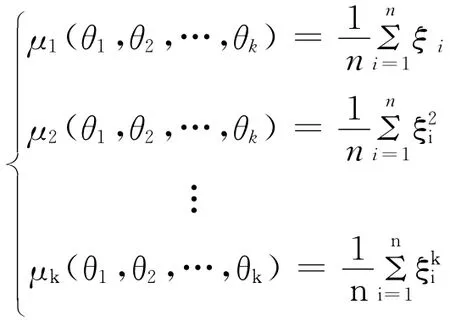
求这个方程组的解，得θi＝θi（ξ1，ξ2，…，ξn），（i＝1，2，…，n），于是未知参数θi的估计量为＝θi（ξ1，ξ2，…，ξn），（i＝1，2，…，n）。

例 假设随机变量X服从区间［a，b］上的均匀分布，参数a，b未知，X1，…，Xn是来自X的一个样本，求参数a与b的矩估计。

解 首先，我们需要将被估计的参数a与b分别表示为总体矩的函数。记EX＝μ，DX＝σ2则有

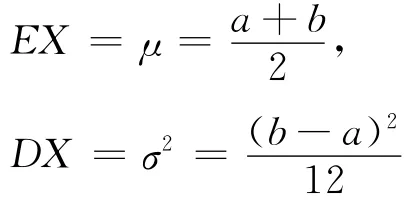
于是可以建立关于a与b的方程组

解出

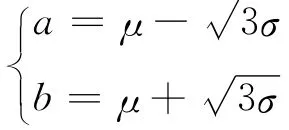
因此 a与b矩估计分别为

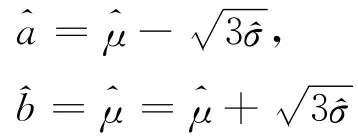
其中

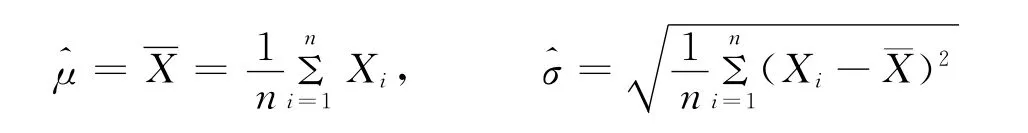
当进行矩估计时，如果被估计的参数不是总体矩本身而是总体矩的函数时，应该首先将被估计的未知参数θ表示为总体矩的函数，然后再用样本相应矩的同一函数θ作为该参数θ的矩估计，这往往是矩估计方法的关键所在。

［1］中山大学数学力学系.概率论及数理统计［M］.北京：高等教育出版社，1980.

［2］周概容.概率论与数理统计［M］.北京：高等教育出版社，1984：378.

［3］盛 骤.概率论与数理统计［M］.北京：高等教育出版社，2004：189.